
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
细长钢筋混凝土构件耗能性能评价及其应用
太圣欧姆,香港公园
摘要:钢筋混凝土构件的耗能是决定其抗震性能的基本结构能力之一。根据以往的研究,在反复循环加载过程中,钢筋混凝土构件的耗能主要是由钢筋的塑性行为而不是混凝土发展而来的,混凝土是一种脆性材料。在本研究中,通过对塑性铰区域的分段分析,对柔性为主构件的耗能机理进行了重新评价。基于能量耗散机制,建立了简化方程来评价细长柱、梁和墙的能量耗散。
关键词: 能量消耗、应变能钢筋混凝土
简介:钢筋混凝土构件的耗能是决定其抗震性能的基本结构能力之一。在现有的非线性静态方法中,每个荷载循环的耗能能力被用来评估结构的非弹性地震反应,包括地震荷载、层位漂移和顶板位移[1-8]。此外,对钢筋混凝土构件进行了大量的循环荷载试验和数值研究,并对其耗能进行了报道。然而,由于钢筋混凝土构件表现出复杂的循环行为,包括挤压和刚度退化,因此能量耗散的预测方法尚未见报道。因此,对于耗能能力的评价,本设计建议和指南采用经验方法,可能不够准确;结构的耗能能力是根据结构类型和材料规定的,而不考虑结构的设计参数[1-8]。最近,Eom[16]研究了细长钢筋混凝土构件(梁、柱、墙)在循环荷载作用下的耗能机理。他们报告说,钢筋混凝土构件的耗能受到各种设计参数的影响,包括配筋率、配筋布置、塑性变形的大小。这一结果表明,应考虑设计参数,以准确评价耗能。在本研究中,对钢筋混凝土细长构件的耗能机理进行了重新评价,以量化耗能。基于能量耗散机制,建立了简化的方程,使细长构件的能量耗散可以方便地计算,而无需对循环行为进行详细的分析。
研究范围:根据Eom的说法,总体包络曲线下的面积表示,循环曲线所包围的面积表示。利用单调荷载-位移曲线和最大变形可以很容易地计算,另一方面,其评价需要对钢筋混凝土构件的循环行为进行详细的分析,考虑弯曲挤压和刚度退化的影响是由轴向压缩和不对称钢筋布置在截面上的影响发展而来的。作为评价钢筋混凝土结构耗能的基础研究,本研究的重点是具有足够加固细节的细长构件的耗能,其表现出弯曲为主的稳定循环行为。钢筋细节不足或极大的非弹性变形可能导致各种破坏机制,包括剪切破坏、钢筋屈曲和粘结滑移,从而降低能量耗散。所提出的方法不应用于循环行为受到这种失效机制显著影响的成员。
钢筋混凝土构件的耗能机理:
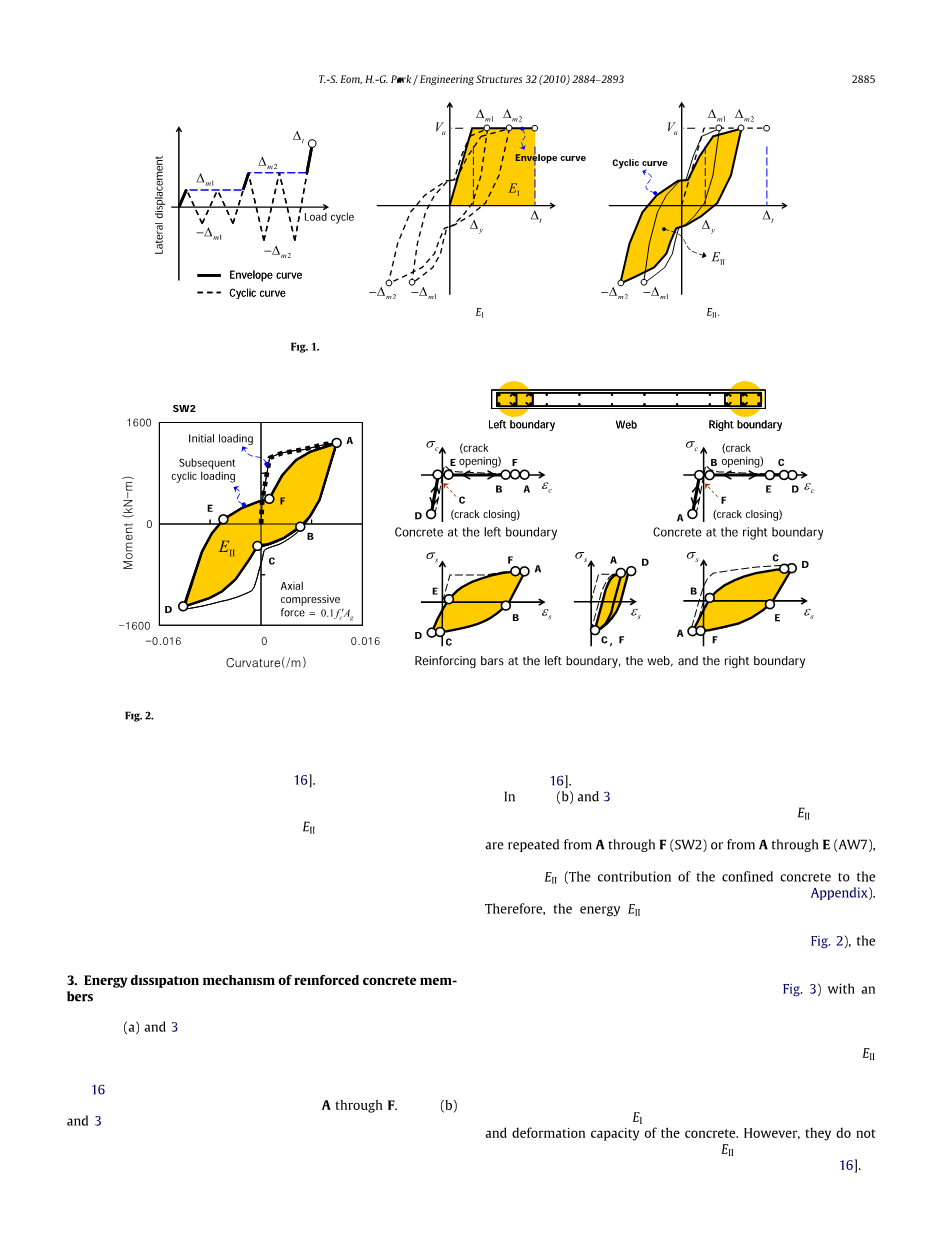
2(a)和 3(a)显示了由非线性数值分析产生的具有对称和不对称配筋布置的柔性主导钢筋混凝土构件(SW2和AW7)的典型循环矩-曲率关系[16]。在这些数字中,强度和刚度显著变化的主要点被表示为A到 F。2(b)和 3(b)显示了混凝土和钢筋在构件中的循环应力-应变关系。主要点也在应力-应变曲线中标明。在混凝土和钢筋的应力-应变关系中,对于柔性为主的钢筋混凝土构件的耗能机理,可以观察到以下几个重要方面[16].在2(b)和 3(b),应力-应变关系中由滞环包围的面积表示每种材料耗散的能量EII。如图所示,当从A 到 F(SW2)或从A到 E(AW7)重复循环荷载时,混凝土是一种脆性材料,不会显著消散 EII(详细讨论了约束混凝土对能量耗散的贡献)。因此,钢筋混凝土构件的能量EII主要由弯曲钢筋耗散。在具有对称加固布置的构件中(SW2,2)在横截面的两个边界处的钢筋都会消耗相当大的能量,因为它们都经历了很大的磁滞回线。另一方面,在一个成员(AW7,图3)不对称钢筋布置,具有较大截面面积的钢筋在重复荷载循环过程中保持弹性,因为压缩钢筋和张力钢筋之间的力平衡。因此,耗能 EII主要发生在面积较小的钢筋上,经历了较大的滞后环。
4.能量耗散评价EII
图4为a的应力-应变关系的全循环钢筋。的单位体积耗散的能量钢筋可以计算UII=2RBfyhε1ε2εyi(2)式中UII为钢筋,RB为折减系数Bauschinger效应(=0.75,[16]),fy和εy分别为屈服应力和ε1和ε2分别为最大值和最小值钢筋在完全荷载作用下所经历的应变周期,分别。如果钢筋保持弹性,它就会保持弹性在循环加载过程中不会耗散能量。因此,在Eq.(2)中,当微分应变(ε1ε2)时,hε1ε22εy=0筋量小于2εy。式(2)中,钢筋的耗能密度为定义为微分应变的函数(ε1 ε2)。因此,若得出钢筋的最大和最小应变说明在一个完整的负载周期的经验估计,能量钢筋混凝土构件的耗散EII,主要是由钢筋贡献,可进行计算。自钢筋的最大和最小应变根据钢筋在截面上的布置,得到能量耗散EII分别对对称和不对称配筋布局。
4.1 构件采用对称的加固布置
以其为主的受弯柱或矩形截面墙的典型弯矩-曲率关系为如图2(a)所示。不受轴向作用的梁压缩力可以看作是这种类型的一种特殊情况成员。图5(a)显示了矩形截面的应变剖面,在a期间产生最大和最小应变。图2(a)中a - b - c - d - e - f - a的完整负载周期。在图中,如—边界钢筋截面积;海关钢筋质心之间的距离为这两个边界;rho;w是均匀分布的腹板钢筋(=Aw/(hwbw));Aw是截面积腹板钢筋;hw是网络深度钢筋分布;bw是网络的宽度。如图2(a)所示,的最大和最小应变钢筋在A、C(或F)、D、εA、εC、εD处发育。而在C(或F)处的应变剖面εC仅与腹板钢筋的最小应变,其贡献对整体能量耗散的EII明显小于钢筋的边界。因此,应变剖面将在截面上发展出的最大和最小应变简化为εA和εD,对应最大值分别在正方向和负方向的曲率。因此,截面钢筋的微分应变计算公式为|εA εD|。εA和εD的应变分布,得出εA和εD的位置中立轴的计算需要采用截面分析。然而,对于一个对称的截面配筋排列时,实际差分应变|εA εD|可以用对称微分应变|(phi;m phi;m)x|代替采用截面分析,其中phi;m 和phi;m(gt;0)最大正方向和负方向的曲率,x是到截面中心的距离。这是由于差分应变|εA εD|和|(phi;m phi;m)x|导致对称截面的能量耗散相同。钢筋耗散的能量密度为计算用(phi;m phi;m)x式(2)中ε1ε2。然后,截面整体能量耗散eII(图2(a)循环弯矩-曲率曲线围成面积)可以通过积分能量密度UII除以横截面。
4.2 具有非对称补强排列的构件
图3(a)为a的循环弯矩-曲率关系梁与非对称钢筋排列,展示具有不对称夹紧的循环行为。图6显示了边界处产生的最大和最小应变图6所示。非对称加固截面的能量耗散安排。钢筋在加载周期a - b - c - d - e - a如图3(一个)。最大和最小应变发生在A和C由最大正曲率和负曲率组成,εA和εC。如图3(b)所示,具有非对称的强化布置主要由钢筋的边界面积较小。因此,为了估计光束的能量耗散EII,微分面积较小钢筋应变∆ε2 (=|εA εC |)。需要评估(见图6)。然而,由于包辛格,∆ε2,难以准确估计。因此,∆ε2钢筋通过假定近似估计具有完美的弹性塑性行为。在A处(图3(A)和6),钢筋的面积更大As1受拉屈服。通过反向加载C,这些钢筋受到压缩,和面积As2较小的钢筋受拉。面积较小的钢筋在C处受拉时屈服。因此,面积较小的钢筋的受拉力为定义为TC = fyAs2 = Esεy As2 (5)式中,Es为钢筋弹性模量。另一方面,面积较大的钢筋为1在c处不屈服并保持弹性钢筋,从A到C卸载,可以计算的CC =minus;fyAs1 Es∆ε1As1 = Es∆ε1 εyAs1。(6) 利用CC和TC之间的力平衡,进行了微分面积As1较大钢筋的应变∆ε1可以为计算为∆ε1 =1 As2 As1εy。(7)其中,由于As1ge;As2,∆ε1小于2εy,说明面积大于As1的钢筋不耗能(见Eq(2))。因此,在钢筋混凝土构件中带有非对称加固布置,只有加固在此过程中,面积As2较小的棒材消耗能量eII(或eII)反复循环荷载。钢筋的微分应变∆ε2面积As2可计算为(图6)。虽然式(9)是为非对称的公制配筋安排截面而制定的,但它也可以用于对称配筋安排(As1 = As2)的截面。For As1 = As2 = As,式(9)与式(3)中的第一项相同。4.3。钢筋混凝土构件的耗能EII和结构在细长构件中,由于非弹性而引起的能量耗散塑性铰区域的行为发展。的能量塑性铰的耗散EII可以通过积分计算得到塑性铰截面上的能量耗散eII长度。假设塑性铰的平均曲率phi;m计算得到塑性铰的能量耗散EII作为EII = EII lp (10)式中lp为塑性铰的长度。通过插入方程式。(3)、(4)、(9)为式(10)中的能量塑性铰的耗散EII可计算如下: EII = EII lp (10)式中lp为塑性铰的长度。通过插入方程式。(3)、(4)、(9)为式(10)中的能量塑性铰的耗散EII可计算如下:EII = 4RBfy theta;m theta;m hs2 2εylp As 4RBfy theta;m theta;mEII = 4RBfy theta;m theta;m Ds 2pi; εylprho;pi;4d2(b 11日EII = 2RBfytheta;m theta;mhs 3 As2 As1εylpAs2 (11c)theta;m (=phi;m lp)和theta;m (=phi;m lp)是塑料处的旋转铰链。一般情况下,式(11a)可用于柱和墙具有矩形截面并在腹板中有钢筋的。式(11b)必须用于圆形柱。式(11c)可以是适用于有顶有底的矩形或t形梁截面上的钢筋(11a) - (11c)可以用来计算能量耗散整体能量耗散EII可以通过简单地将所有能量相加来计算单个塑料铰链的耗散。然而,如果强化图7所示。悬臂梁的位移和曲率。梁柱节点处的粘结滑移和剪切变形对结构的整体性能有显著影响方法不应用于该结构。考虑钢筋粘结滑移的影响还需要进一步的研究及梁柱节点处的剪切变形。
5. 对所提方法的验证
提出了一种能量评价方法对83个试件(包括柱、墙和梁[17-41]。试样的性能表1简要总结了。这些标本受双曲率作用的悬臂或构件。的将具有双曲率的构件理想化为半跨距受单一曲率作用的悬臂。为了评估每个负载循环的能量耗散EII每一个悬臂构件的最大正负塑性铰处的曲率,phi;m 和phi;m,计算为遵循。如果曲率沿悬臂长度的分布为假设如图7所示,最大曲率在固定处结束phi;0米塑性铰的平均最大曲率phi;m可以计算为ϕ0m =∆m m∆y lp(l lp/2) ϕand phi;m =phi;0m phi;y lp2l(12)其中,∆m为自由端横向位移,∆y (=phi;yl2/3)为屈服位移,phi;y为屈服曲率。细长构件的塑性铰长度是可以估计的对于矩形截面,lp = h/2,a=D/2圆形截面[3]。可以估算出收益率曲率phi;y = alpha;ST εy/h,其中h为截面深度,εy为受弯钢筋的屈服应变,alpha;ST为代表构件类型和截面的系数柱形:矩形截面柱alpha;ST = 2.12圆形截面柱为2.35,圆形截面墙为2.00截面为矩形,梁[4]为1.70。利用式(12)计算塑性铰非弹性转动theta;m (=phi;mlp)。的能量耗散EII使用方程式计算成员。(11a)、(11b)或(11c)。图8比较了能量耗散EII和等效阻尼比beta;eq(一种标准化的能量耗散)预测提出的方法与试验结果一致。等效阻尼根据所提供的计算方法计算了beta;eqATC-40 [1]: beta;eq = 0.05 EII/(4pi;ES0)其中ES0最大构件的应变能。平均值和标准结果表明,预测值与试验值的比值有较大的偏差在图8所示。如图所示,本文方法预测了能量耗散EII和等效阻尼比beta;eq合理的精度。
6. 所提方法的应用
应用一:能量循环模型。本文提出的基于能量的钢筋混凝土构件的弯矩-旋转关系可以简化定义循环模型,以一种方式使区域被a包围循环曲线与预测的滞回能量一致EII。图9给出了a的循环M -theta;关系塑性铰。如图所示,使用了两种类型的曲线-envelope曲线和循环(卸载/重新加载)曲线来描述循环力矩-旋转关系。用弹性刚度定义了单调荷载下弯矩-转动关系的envelope曲线柯,屈服力矩My,屈服旋转theta;y,屈服后刚度ness Kp。循环曲线描述了卸载/再加载be在当前最大值和最小值之间重复的行为变形。如前所述,循环曲线的定义是这样的被循环曲线包围的能量与预测能量相同每负载周期耗散EII。循环曲线见图9连接关键点a、b、c、d的集合,构成a平行四边形。对于塑料铰链,EII可以用下列方法计算方程式。(11a)、(11b)或(11c)。然后,旋转和力矩点b和e (theta;b, Mb)和(theta;d, Md)可由简单的代数运算。为验证所提出的能量循环模型应用于钢筋混凝土梁、柱和墙(图10)。由于试件为悬臂梁,在根据式(12)计算塑性铰theta;m (=phi;mlp)。的得到了theta;y = phi;ylp和phi;y = alpha;ST的屈服旋转εy / h[4]。屈服后刚度Kp近似设为0.01克。对于压缩构件,存在二阶效应将弯矩承载能力修改为(M P∆)。其中,∆为的自由端横向位移悬臂成员。然
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[265158],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


