
英语原文共 12 页,剩余内容已隐藏,支付完成后下载完整资料
钢筋混凝土短耦合梁的能量循环力-位移关系
Tae-Sung Eom,Hong-Gun Park,Su-Min Kang
大邱天主教大学建筑系,韩国
首尔国立大学建筑系,韩国
伊莱姆工业公司,韩国
摘要:本文研究了不同配筋方式下短连梁的循环力-位移关系和能量耗散,为连梁的非弹性分析提供了参考。首先,采用非线性桁架模型分析了短连梁的循环性能。数值分析结果表明,短连梁的滞回能量主要由斜配筋耗散,而不是由混凝土和常规的纵向和横向配筋耗散。在此基础上,提出了各种配筋方式下短连梁能量耗散和力-位移关系的简化预测方法。滞回耗能计算方法为斜向钢筋的塑性耗能之和。循环力-位移关系的定义是,循环曲线所围成的面积与预测的滞回能量耗散相等。为了验证该方法的有效性,将该方法应用于现有的试件。
关键词: 耦合的墙;循环加载;能量耗散;非线性分析;钢筋混凝土;桁架模型
1 简介
钢筋混凝土耦合墙已被用作受地震荷载作用的建筑结构的有效抗侧向荷载系统。对耦合墙系统进行非弹性分析时,应确定耦合梁的循环力-位移关系。然而,由于短连梁具有复杂的受剪特性和多种受剪配筋布局,其循环性能难以预测,而短连梁对剪力墙的整体结构性能有显著影响[1-9]。虽然非线性有限元分析模型[10-15]或非线性桁架模型[16,17]可以用于预测循环行为,但它们需要复杂的建模技术和巨大的计算工作。因此,需要一种更简化的方法,利用短连梁的设计参数来预测其循环力-位移关系。
在传统的框架结构非线性分析,各种滞回模型包括克劳夫和武田模型[21]已经经常用于描述钢筋混凝土构件力-位移关系的循环(DRAIN-2DX[22]和IDARC-2D[23])(图1)。这些模型可分为基于刚度退化模型,因为他们专注于描述构件刚度。在这些模型中,降低的卸载/再加载刚度是根据相关实验证据或工程师的经验来确定的。然而,由于短连梁的卸载/再加载刚度在循环加载过程中变化显著,且根据配筋布置的不同,在没有试验证据的情况下很难预测其卸载/再加载刚度的详细变化。图2为钢筋混凝土构件的循环力-位移关系。循环曲线所围成的区域表示荷载循环[24]耗散的滞回能EII。从滞回能出发,可以将循环力-位移关系定义为循环曲线所围成的面积与滞回能相等。如果能利用构件的设计参数准确计算出其能量,则可以在不依赖试验证据或复杂的非弹性分析的情况下预测循环力-位移关系。此外,在非线性静地震设计方法中,如能力谱法[25,26]和直接位移设计方法[27],可以使用量化的能量耗散从非弹性设计反应谱确定地震荷载。本文提出了一种基于滞回耗能的短连梁(0.75le;剪力跨高比le;1.25)循环力-位移关系预测方法。为此目的,进行了以下研究。(1)采用非线性桁架模型分析方法,研究了不同配筋方式下短连梁的耗能机理;(2)根据计算结果,提出了一种预测耦合梁滞回耗能的简化方法;(3)基于量化的滞回耗能,预测短连梁的循环力-位移关系。
图1 现有的钢筋混凝土构件滞回模型;基于退化刚度的模型
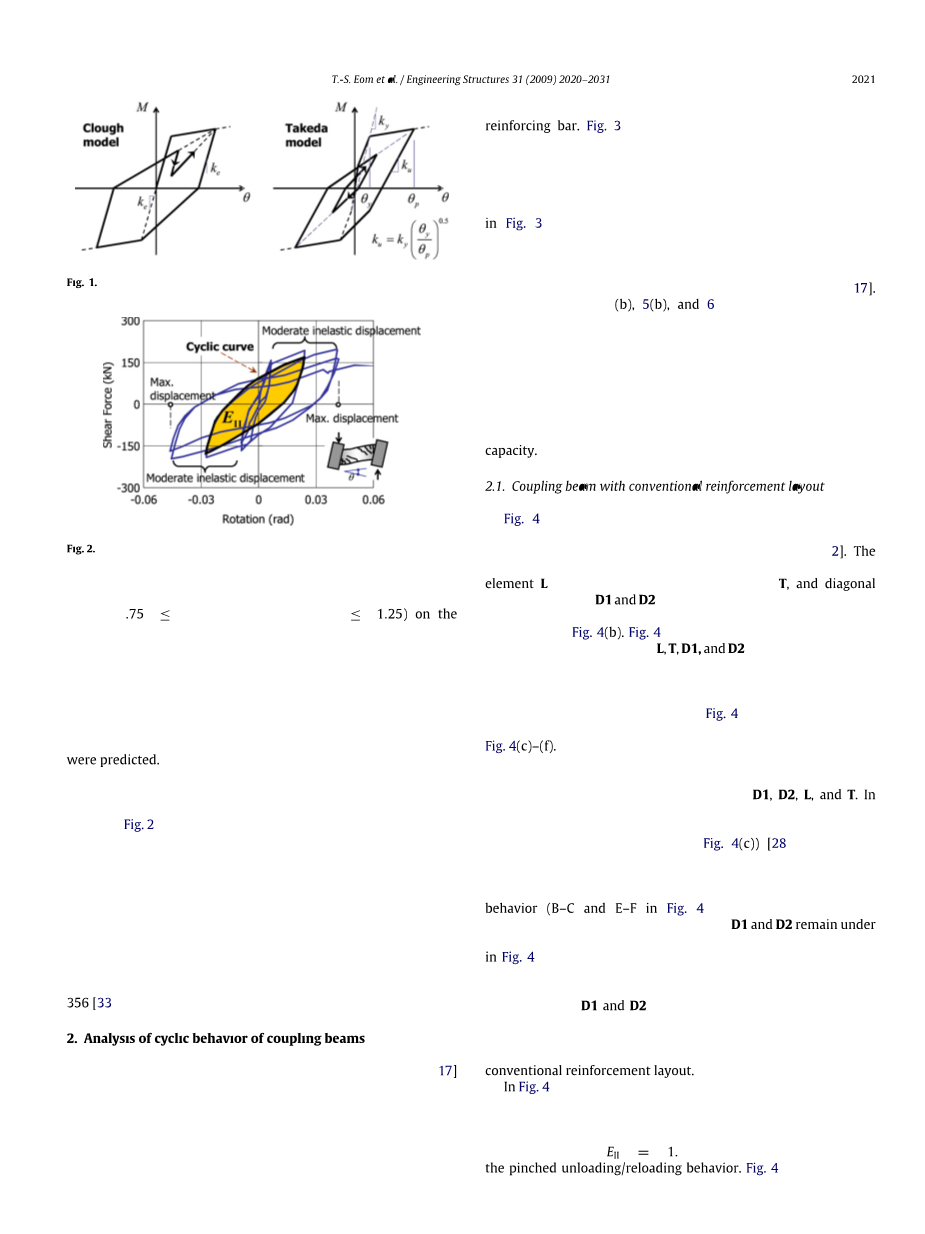
图2 钢筋混凝土短耦合梁的滞回耗能
在目前的研究中,我们集中在评估中等塑性变形下的循环力-位移关系,使用桁架模型的荷载传递机制。然而,如图2所示,在耦合梁最大位移时,由于混凝土破碎、混凝土拉伸断裂、钢筋屈曲等脆性破坏机制,其承载能力和耗能显著降低。因此,本文所提出的方法必须仅适用于中等塑性变形时的荷载-位移关系。为了完全确定荷载-位移关系,应该通过考虑脆性破坏模式来预测耦合梁的最大变形(或变形能力)。耦合梁的最大塑性变形可以根据FEMA-356[33]准则或实验结果进行估计。
2 .耦合梁的循环性能分析
采用Park和Eom[17]建立的非线性桁架模型,研究了短连梁在横向循环荷载作用下的耗能机理。非线性桁架模型是方便评估钢筋混凝土构件的性能,因为分析结果表示为桁架单元的单轴力-位移关系,而不是分布的混凝土和钢筋的多维应力-应变关系。图3为钢筋混凝土耦合梁的非线性桁架模型。耦合梁是理想化的纵向、横向和对角桁架单元,每个单元由混凝土和钢筋组成。在每个桁架单元中使用的混凝土和钢筋的循环应力-应变关系也显示在图3中。应力-应变关系描述了混凝土的循环拉压性能,混凝土的压缩软化性能由于横向受拉裂缝的共存,以及钢筋的包辛格效应。在Park和Eom[17]中详细说明了建模技术。如图4(b)、5(b)和6(b)所示,在中等非弹性变形时,耦合梁表现出稳定的循环性能,强度退化不明显,非线性桁架模型分析对耦合梁的整体循环性能具有合理的预测精度。然而,在最大非弹性变形时,由于混凝土破碎、钢筋屈曲或钢筋粘结滑移而发生显著的强度退化。因此,非线性桁架模型分析高估了桁架的承载能力和耗能能力。
2.1 联梁采用常规钢筋布置
图4(a)为Galano和Vignoli[2]试验P02试件的钢筋细部、非线性桁架模型以及混凝土和钢筋的材料性能。非线性桁架模型由纵向钢筋单元L、横向钢筋单元T和斜向混凝土单元D1和D2组成。图4(b)将非线性桁架模型预测的力-位移关系与试验结果进行对比。图4(c) - (f)为非线性桁架模型分析得到的单元L、T、D1、D2的循环应力-应变关系。为了研究耦合梁的循环性能,在循环加载过程中耦合梁刚度和强度发生显著变化的关键点用图4(b)中的字母A到F表示。图4(c) - (f)中元素的应力-应变关系也标出了关键点。
在短耦合梁与传统的纵向和横向钢筋布置、横向荷载抵制桁架机制提供的D1、D2、L和t.耦合梁承受反复循环荷载,由于发生纵向伸长残余塑料拉伸压力的纵向钢筋(图4 (c))[28]。由于这种纵向延伸,随着循环加载的进行,斜向拉伸裂缝逐渐扩大。因此,在卸载/再加载过程中,沿对角拉伸裂缝发生剪切滑移(图4(b)中的b - c和E-F)。在剪滑变形过程中,混凝土斜杆D1和D2仍处于受拉状态,不抵抗压力(图4(e)和(f)中的B-C和e - f)。因此,联轴梁失去刚度,不能传递剪力。随着剪切变形的加剧,C、F点处的斜向张拉裂缝完全闭合后,D1、D2开始产生压缩力。结果,联轴器梁恢复刚度,并抵抗横向荷载。这种构件刚度的损失和恢复导致了传统配筋布局的短耦合梁的挤压循环行为。
图3 非线性桁架模型
图4 采用常规配筋布置的P02联轴梁的循环性能:(a)尺寸和桁架模型;(b)循环力-位移关系;(c) - (f)混凝土和钢筋单元的循环应力-应变关系。
在图4(b)中,循环曲线A-B-C-D-E-F所围成的区域表示耦合梁的滞回耗能。如图所示,由于卸荷/再加载行为的压缩,采用常规配筋布置的耦合梁仅耗散了非常小的滞回能量(P02的EII = 1.00 kN m)。图4(c) - (f)显示了混凝土支柱和钢筋的能量耗散。混凝土斜杆D1和D2在循环荷载作用下承受较大的非弹性拉压应变。然而,由于混凝土的脆性特性,混凝土支柱的滞回能量耗散(循环应力-应变关系曲线所围成的区域)可以忽略不计(见图4(e)和(f))。此外,纵向钢筋L和横向钢筋T都不有助于滞回能量耗散EII,因为它们的应力和应变在循环加载期间仍处于受拉状态(图4(c)和(d))。因此,采用常规配筋布置的耦合梁在循环加载过程中不会显著耗散滞回能量。
2.2 采用对角钢筋布局的耦合梁
图5(a)和图6(a)为Galano和Vignoli[2]测试的试件P07和P14的混凝土和钢筋的钢筋细部、非线性桁架模型和材料性能。P07和P14分别采用x型和菱形加固布局。图5(b)和图6(b)将非线性桁架模型预测的力-位移关系与试验结果进行对比。图5(c) - (f)和图6(c) - (f)分别给出了钢筋单元sl、D1、D2和混凝土对角单元D3的循环应力-应变关系。图5和图6中没有显示横向钢筋单元T的循环应力-应变关系,因为它与图4(d)中采用常规配筋布置的联梁几乎相同。耦合梁刚度和强度显著变化的关键点用图5和图6中的字母A到F表示。
如图5(b)和6(b)所示,采用对角钢筋布置的耦合梁耗散了相当多的滞回能量(P07的EII = 8.42 kN m, P14的EII = 7.54 kN m),表现出稳定的循环性能,且无箍缩。与采用常规配筋布置的联梁相似,采用斜向配筋的联梁由于纵向和斜向配筋的残余应变也经历了纵向延伸(图5(c)和6(c))。由于这种纵向延伸,在从A点到C点的卸载/再加载行为期间,D3对角混凝土支柱仍然处于受拉状态,并没有抵抗压力(图5(f)和6(f))。另一方面,D1和D2较早表现出塑性行为,在拉伸应变下产生压缩屈服应力,并在循环加载过程中耗散大量的滞回能量(图5(d)和(e)以及图6(d)和(e))。在P07和P14中,斜向钢筋分别耗散了总滞回能量的85%和70%。因此,采用斜向配筋的连接梁比采用常规配筋的连接梁耗散的滞回能量要大得多。
在x型配筋布局的联梁中,由于纵向延伸,L在循环加载过程中仍处于受拉状态,且不耗散滞回能量(图1)。5 (c))。另一方面,在采用菱形钢筋布置的耦合梁中,L对滞回耗能有贡献(图6(c))。但所有纵向配筋对P14整体滞回耗能的贡献仅为6.5%,明显低于斜配筋的贡献。纵向钢筋的低能量耗散表明短连梁的非弹性变形主要是由斜向受拉裂缝的剪切作用引起的。
3.滞回耗能
如上所述,在重复循环荷载作用下,采用常规配筋布置的联轴梁不会耗散滞回能量。另一方面,采用x型或菱形斜向配筋的联轴梁耗能较大,滞回能量主要由循环荷载作用下的斜向配筋产生。因此,本文的研究重点是评价斜向钢筋的滞回能量耗散。
根据Park和Eom[24],单位体积钢筋耗散的应变能密度ui可由钢筋的屈服强度和钢筋在加载循环过程中所经历的微分应变(ε1 ~ ε2)计算得出(图7)。
式中fy为钢筋屈服应力,εy为钢筋屈服应变;ε1、ε2分别为钢筋在一个荷载循环中所受的最大应变和最小应变;RB为考虑包辛格效应的还原因子(=0.75,[24])。
在式(1)中,应预测最大和最小应变,以评估钢筋的能量耗散。如图5和图6所示,耗散耦合梁滞回能量主要部分的斜向钢筋在横移正负峰值A点和D点应变最大和最小。因此,根据非线性桁架模型在横向位移峰值处的变形形状来预测斜向钢筋的最大和最小应变。
图8(a)和(b)分别给出了采用x型配筋布置的联轴梁的桁架模型和变形形状。图中lb为耦合梁的长度;hD为lD横向分量;lD和ADs分别为斜向钢筋单元的长度和面积;alpha;为钢筋对角单元与纵轴的夹角。在图8所示的桁架模型中,只考虑了两个对角钢筋单元D1和D2的变形,因为这些变形消耗了滞回能量的主要部分。在图8(b)中,加载点的横向位移和纵向位移分别表示为u (或uminus;)和v (或vminus;)。上标 和minus;表示横向荷载的方向。在正横向荷载的位移u 和v 处,D1和D2分别具有最大和最小的应变;在负横向荷载作用下,位移uminus;和vminus;处,D1和D2分别具有最小和最大的应变;当耦合梁的循环行为发生在正、负横向位移u 和uminus;时,对角钢筋单元的ε1和ε2的计算公式如下:
对D1来说
对D2来说
如图5(c)所示,在反复循环加载过程中,纵向钢筋单元L仍然处于受拉应力状态,不耗散滞回能量。结果表明:联轴器梁的纵向伸长在v vminus;加载周期内保持在一个均匀水平。因此,D1和D2的差分应变(ε1 ~ ε2)可以简化为
将式(3)代入式(1)即可计算出各对角钢筋单元的UII值,将UII乘以对角钢筋单元体积(=ADslD)即可计算出各对角钢筋单元耗散的滞回能量。耦合梁的滞回耗能EII为各对角钢筋单元耗能之和。
式中fyi、εyi、ADsi为各对角钢筋单元的性质。如果两个对角钢筋单元具有相同的性能,则式(4a)为
菱形配筋梁的滞回耗能计算方法与x形配筋梁的滞回耗能计算方法相同。图9(a)和(b)分别给出了采用菱形配筋布置的联轴梁的桁架模型和节点位移。如图6(f)所示,在反复循环加载过程中,由于联轴梁的纵向伸长,混凝土构件并没有积极参与传力机制。耦合梁的循环性能主要由钢筋单元控制。因此,图9(a)中的桁架模型仅采用钢筋单元进行简化。如图9(b)的变形形状所示,菱形配筋布局中的每根斜向钢筋都可以建模为与x型配筋布局相同的半跨长度的斜向钢筋。因此,通过将式(3)中的u 和uminus;分别替换为u /2和uminus;/2,可以计算出各对角杆单元的微分应变(ε1 ~ ε2)。利用微分应变,由式(1)求出单位体积钢筋耗散的ui,然后,然后,采用菱形配筋布局的联梁EII的计算方法是将ui乘以四个对角配筋单元的总体积(=4ADslD)。
如图6(c)所示,在循环加载过程中,纵向钢筋也会耗散滞回能量。然而,在本研究中,由于纵筋耗散的能量远远小于斜筋耗散的能量,因此忽略了纵筋耗散的
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[265155],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


