
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
第9届IFAC会议关于海洋系统中的控制应用
国际自动控制联合会
2013年9月17-20日 大阪 日本
用SISO法设计大型柴油机的可实现性能--废气再循环控制
Jakob Mahler Hansen1,2 Mogens Blanke1,3
Hans Henrik Niemann1 Morten Vejlgaard-Laursen2
(1.丹麦技术大学 电气工程系 灵比 丹麦;
2.MAN Diesel amp; Turbo(公司名称) 哥本哈根 丹麦;
3.AMOS CoE 挪威科技大学控制论研究所 特隆赫姆 挪威)
摘 要:本文研究了大型采油机废气再循环(EGR)的控制可能性。目的是通过降低可用于燃烧的氧气浓度来减少废气中的NXO的量。使用高等非线性动力学的线性分析来评估系统施加的控制极限。研究了控制结构,并在模型不确定的情况下研究了抗扰性和参考跟踪方面的性能。使用经典和定量反馈理论(QFT)设计来研究古典前馈和反馈控制器设计。控制器的验证在模型上进行,重点是扰动减少能力。
关 键 词:废气再循环 柴油发动机 绿色船 鲁棒 定型反馈
1.介 绍:
废气再循环(EGR)可以通过减少进入内燃机的进气中的O2浓度来减少发动机排气。本文考虑了对大型二冲程柴油发动机的EGR过程的控制,重点是该过程中的控制挑战和可获得的性能。本文针对单输入单输出(SISO)方法。
由于环境问题,国际海事组织(IMO)发布了一系列限制柴油发动机允许排放的协议。这些协议被称为TierⅠ,Ⅱ和Ⅲ,设计NOX,SOX和温室气体的排放。Ⅰ和Ⅱ方案是全球限制,分别于2000年和2011年采用。TierⅢ协议适用于2016年排放控制区的NOX。
EGR技术在燃烧中重新使用发动机排出的废气,以便减少发动机进气中的氧气量,从而减少在发动机中产生NOX的量。对于多少废气可以再循环而没有剥夺发动机用于燃烧的足够的氧气存在上限。
大多数关于EGR技术的科学文献涉及四冲程汽车发动机。EGR过程的非线性动力学难以建模,但是Wahlstrbull;om and Eriksson [2011b]用卡车发动机实验与实际数据拟合良好。几个研究者Al eri et al. [2006], Chen和Wang [2012]研究过了模型的反馈,但这些方法需要在操作范围内非常精确的模型。Colin et al. [2011]等专注于研究鲁棒控制,使用线性常数控制显示哪些性能可以用驱动条件的线性方法实现。最近在Wang [2011a,b]等人的线性稳健设计中处理了可变集合涡轮机和EGR的控制。Kotman et al[2010],Wahlstrbull;om and Eriksson [2011a]等使用非线性方法研究出良好的结果,但是需要非线性动力学模型,而精度不可用于二冲程发动机。
本文首先介绍了一个实验性验证的非线性模型。通过模型参数对模型进行不确定性的研究。控制结构以经典控制为基础,然后设计和补充定量反馈理论(QFT)方法来应对鲁棒性问题。
- 模 型:
EGR系统中的发动机是具有四个气缸的二冲程柴油4T50ME-X发动机。发动机的进气口由可变几何涡轮增压器(VGT)提供,可变几何涡轮增压器由位于同一轴上的压缩机和涡轮机组成。发动机的废气通过涡轮机,涡轮机又驱动压缩机,向发动机提供加压的环境空气。
在系统中存在测量压力的两个歧管:扫气空气歧管位于发动机的进气口处;排气歧管位于发动机的输出处。扫气压力必须高于二冲程发动机的排气压力。
EGR回路连接两个歧管,其中鼓风机提供从排气到扫气歧管的质量流。废气通过洗涤器,冷却单元,鼓风机和阀。必须确保鼓风机快速旋转以克服气管之间的压力比。
假定模型中的两个冷却单元理想地将进入气体的温度降低到指示水平,而不影响质量流量。
输入信号是:换向阀(COV)的打开uegr ,以及EGR-鼓风机的速度omega;blow.。干扰是:VGT的打开uvgt,和发动机负载uload。发动机的主要控制变量,用于控制发动机扭矩的转速并因此用于控制轴速度的发动机负载被认为是测量的干扰。期望控制清除氧浓度Oscav。
发动机模型如图1所示,其中输入和干扰用倾斜箭头标记。在发动机上测量的信号下加下划线。
图1.EGR系统的模型结构,测量的扰动包括两个控制输入(uegr 和 omega;blow)和两个输入(uvgt 和uload)
Fig. 1. Model structure of the EGR system. There are two control inputs (uegr and omega;blow) and two inputs (uvgt and uload) that are measured disturbances.
2.1非线性状态空间模型
已经得出一个非线性状态空间模型,由七个微分方程方程和两个差分方程方程组成。这九个状态可以在表A.1中看到。这两个离散状态源自Wahlstrbull;om和Eriksson[2011b]建议的废气温度表现。
关于发动机系统建模的主要发现在这里总结,参见Hansen et al [2013]详细的模型描述。发动机质量流量进气被建模为通过节流的质量流量。通过压缩机和涡轮机的质量流量通过使用多项式已经被最小二乘方拟合到映射。通过EGR回路的质量流被建模为通过具有可变开口的压缩机的质量流。使用微分方程来描述两个歧管中的压力和氧浓度。
2.2模型拟合
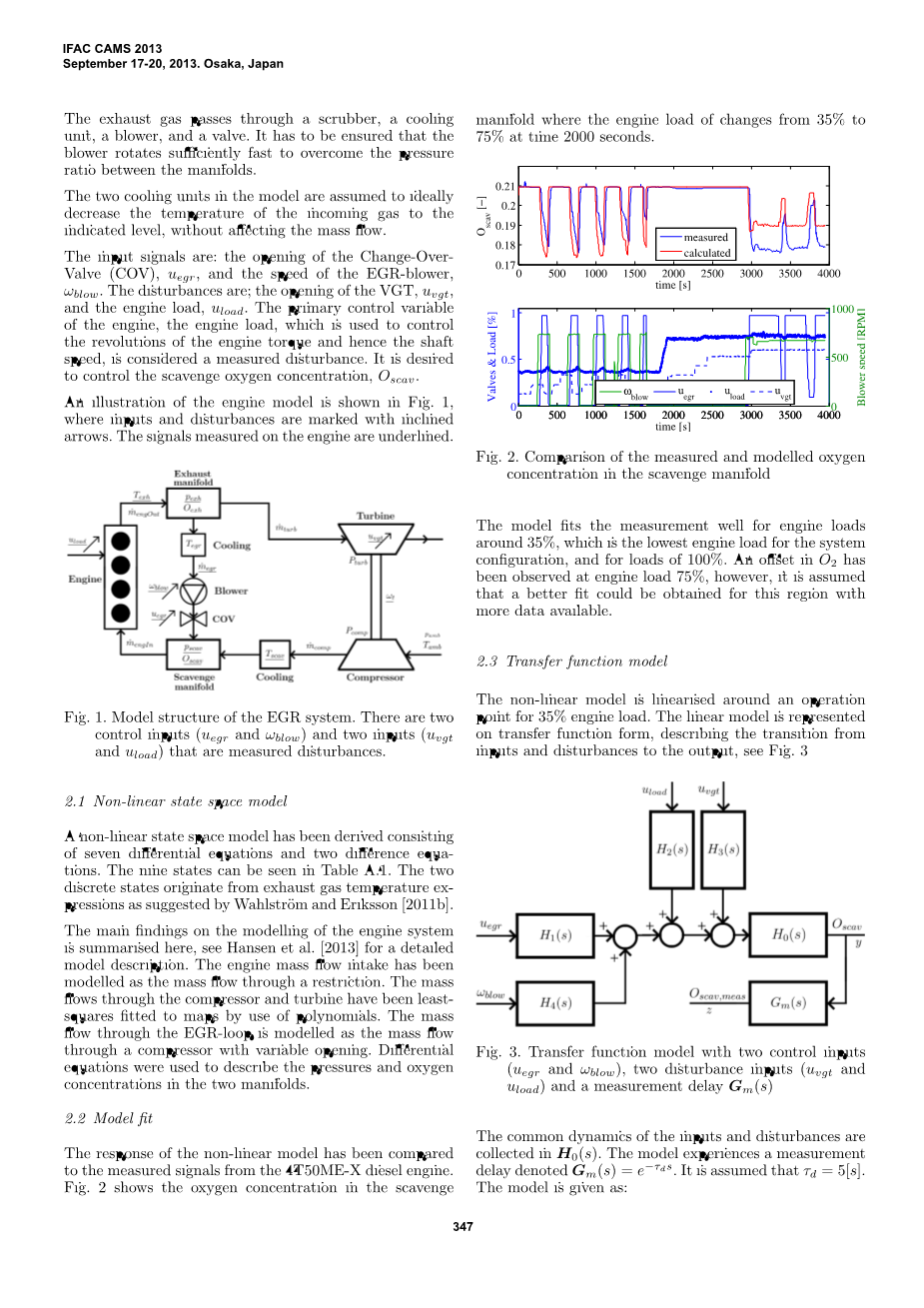
将非线性模型的响应与来自4T50ME-X柴油发动机的测量信号进行比较。图2示出了扫气歧管中的氧浓度,其中发动机负载在时间2000秒从35%变化到75%。
图2.扫气歧管中测得的和建模的氧气浓度的比较
Fig. 2. Comparison of the measured and modelled oxygen concentration in the scavenge manifold
该模型适合发动机负载约35%的测量井,这是系统配置的最低发动机负载,以及100%的负载。在发动机负荷75%时观察到在O2中的偏移,然而,假定对于具有更多数据可用的该区域可以获得更好的拟合。
2.3传递函数模型
非线性模型围绕35%发动机负载的操作点线性化。线性模型表示在传递函数形式上,描述从输入和干扰到输出的过渡,参见图3。
图3.具有两个控制输入的传递函数模型(uegr和omega;blow),两个干扰输入(uvgt和uload)和测量延迟Gm(s)
Fig. 3. Transfer function model with two control inputs
(uegr and omega;blow), two disturbance inputs (uvgt and uload) and a measurement delay Gm(s)
输入和干扰的共同动力学收集在H0(s)中。模型经历表示为的测量延迟。假设模型给出为:
由于两个输入几乎具有相同的动力学,为模型设计的控制器将专注于SISO模型。其中uegr保持不变,留下u=omega;blow。同样,只考虑一种干扰,d=uload,其中uvgt保持恒定。
具有两个传递函数的简化模型如下:
和
被缩放以具有单位的DC增益。这导致两个缩放传递函数,线性化为35%负载。
传递函数以及海浪的近似频率间隔在图4中的波德图中示出。当波浪影响螺旋桨负载并且发动机的轴速度控制(调速器)将对燃料流的校正调节作出反应时,输入将在波频率下变化。因此,控制器对于操作包络上的参数不确定性和变化都是鲁棒的,并且期望它也能够抑制波频率范围中的干扰。使用不同的线性化点模型传递函数变化。对于围绕50%和75%发动机负载的线性化,模型为:
这些传递函数在图4中也有显示:
图4.G(s)和Gd(s)的波特图。波频率间隔用黑线表示。线性化标记为:
为G, 为 G50% 和 为 G75%
Fig. 4. Bode plot of G(s) and Gd(s). Wave frequency interval is indicated with black lines. The linearisations are marked as; for G, for G50% and for G75%.
如果对于在该频率区域中的频率以及在该频率区域中的十年以下的频率,应该抑制干扰,则看起来需要特定的控制努力,如在该频率区域中的。三个线性化之间的差异很小。
2.4模型不确定性
期望控制模型对于模型参数的不确定性是鲁棒的。模型不确定性通过改变特定模型参数进行研究,这第开着的发动机横截面Aeng。参数Aeng表示质量流量计算的不确定性。模型参数的完整列表可以在Hansen等人[2013]的文章中找到。图5和图6分别示出了对于Aeng参数的不同增益的G(s)和Gd(s)的波特图。增益将用于后续图表中的图例。增益1表示标称值。在下文中,标称模型传递函数表示为,和 。
图5.在改变增益的Aeng参数上G(s)的波特图。增益分别为(1.5,1.25,1,0.8,0.66)的五个模型。增益为1表示标称模型。
Fig. 5. Bode plot for G(s) for varying gain on the Aeng parameter. The gains of (1.5, 1.25, 1, 0.8, 0.66) results in five models representing the model uncertainty. A gain of 1 indicates the nominal model.
2.5限制
由于将此调查限于来自O2测量的反馈,所以该测量中的时间延迟对控制器的反馈路径的性能提出了主要限制。反馈路径的交叉频率上的近似上界是(Skogestad和Postlethwaite[1996])。反馈路径因此与时间延迟的倒数成比例地失去动态控制权限。延迟的物理原因是O2传感器可接受的低流速。通过孔口取样获得空气流。设计用于在满负荷时为传感器提供额定流量,因此满排气压力,在较低的发动机负荷下,流量将更小。时间延迟的负载依赖性是反馈路径控制器的可实现性能的另一个关键因素。
图6.在Aeng模型参数上具有变化增益的Gd(s)的波特图。增益1对应于标称值。
Fig. 6. Bode plot for Gd(s) with varying gain on the Aeng model-parameter. A gain of 1 corresponds to the nominal value.
- 控制设计
这里的控制方法是将前馈,从燃料指数到控制输入,与从测量的O2的反馈组合。此外,使用史密斯预测器来减轻传感器死区时间的影响。以下缩写将用于指代这些控制元素:
纯前馈补偿(FF)
经典PI反馈(PI)
QFT反馈设计(QFT)
史密斯预测器(SP)
3.1前馈控制
前馈控制具有不使用Oscav测量并因此不受时间延迟限制的优点。控制器,Kd,的实现可以参照Skogestad和Postlethwaite[1996]see7。
控制器需要满足Skogestad和Postlethwaite[1996]中列出的标准。这意味着控制器完全否定干扰的影响,然而它受干扰传递函数Gd(s)的影响。参考不受控制,因此无法跟踪。从干扰到输出的受控传递函数为:
如图7所示出,来自2.4部分的模型不确定性被以G和Gd引入时的受控模型的波特图。很明显,即使引入模型不确定性,对于波频率的干扰也得忽略。以下控制器研究了帮助前馈控制器排除干扰的可能性。所有以下控制器将采用前馈。
图7.具有不确定性传递函数的FF模型的波特图 全文共9428字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[143739],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


