
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
基于忆阻器的五进制半加法器
摘要:本文将基于记忆系统的三进制加法器电路推广到了基于忆阻器的多值逻辑加法器。通过利用忆阻器的特性和动力学,提出了实现不同编号系统以及提高效率减少处理时间的理论优势。这是基于忆阻器的电路结构来实现的。为了适应更多的逻辑值被处理,存储器应该被量化成更多的电平。五进制编号系统已经被用于证明推广,并给出了推广的过程。最后通过修改电路能够处理不同的编号系统。
关键词:忆阻器,多电平逻辑,五进制,基于忆阻器的加法器
1.简介
因为在半导体产业中晶体管缩放存在物理限制,所以用来提高电子电路性能的新的纳米元件已经出现。最有希望的其中一个元件是缺失的第四个基本元件——忆阻器。在2008年查尔假设并从物理上实现了HP-Lab部分掺杂TIO2。由于其纳米级尺寸和其模拟存储器的能力,忆阻器作为一个新的基本元件为不断变化的硬件提供了巨大的便利,它能够更快更高效的设计硬件电路。
该忆阻器的I-V曲线特征表现为磁滞回线的特性,这意味着它的电阻具有连续的范围。忆阻器是一种状态被存储在其内部的记忆元件,它的变化是通过电荷或磁通量的改变而改变。近年来出现了许多基于忆阻器的逻辑电路,比如:模拟加法和减法电路,数字逻辑电路,二进制逻辑电路,基于三进制和冗余二进制系统的半加法器,和n位冗余二进制全加法器。
忆阻器能应用于数学运算方面,例如一种基于忆阻器的有效位为1的完整加法器同或运算、基于忆阻器的二进制乘法器、使用暗示操作或MAD操作的N位移位加法和乘法器。一个忆阻器和执行逻辑含义的CMOS混合电路显示忆阻器可与CMOS技术兼容。比如可编程MEM计算芯片和忆阻器CMOS HY-电桥、2*2乘法器单元和混合RRAM单元。最近忆阻器的仿真器也出现了。一些仿真器还可以用于数字应用,如基于FPGA的人工神经网络网络。此外,忆阻器还参与了许多应用,如:振荡器,修改的神经元模型,三进制逻辑门,图像理论,以及模糊逻辑处理器。
在忆阻器的众多应用中,忆阻器交叉开关结构不仅可以作为存储器的有效存储或忆阻器的开关结构在许多应用中使用。对于并行算术运算看作为一个非门控阵列取代门控存储器阵列逻辑电路用于神经形态计算的设计、存储器内乘法器,还作为用于估计寄生路径效果的通信信道。
二进制表示的多级算术运算在速度和存储器使用方面具有许多优点。为了方便处理数据,使用编号系统执行算术运算。机器计数用二进制计数(基数2),人类用十进制(基数10)计数。但不是所有的人都用十进制计数,一些古代的文明用不同的编号系统计数。阿兹特克人和玛雅人使用了二十进制 (基数20)计数,古巴比伦人使用六十进制(基数60)计数。亚洲和中国直到相对现代的历史,人们才使用十进制数、印度阿拉伯数字或者罗马尼亚语和汉语非位置数字。
由于在模拟中执行算术运算具有许多缺点。数字运算应运而生,并促进了技术进步。数字在许多应用中具有优势,主要是错误检测和校正。然而,二进制系统被引入去执行数字算术运算;由于晶体管有开和关两个状态,所以会有一个逻辑选择。当探索其他编号系统和发展当今技术的时候,会出现许多优势。
在一个元件中用忆阻器计算大量的数字可以增加算术处理的密度。从理论上来说,一个数字宽度,比如15,在二进制取三个符号表示,可以有唯一的数字忆阻水平,将过程浓缩在一个忆阻器中。五进制体系已被用于表示使用了混合三进制五进制数制的模幂运算。基于符号数字的乘法器多速率转换器的实现被设计为从三进制中取值或五进制中取值。用于十进制的伪随机发生器数字是基于二进制和二进制序列的组合。还有一种量子实现多值Feynman和Toffoli栅极,其包括三进制、四进制和五进制Feynman栅极。
多级逻辑及其应用几乎与二进制逻辑和布尔代数一样都过时了。对忆阻电路进行了理论分析,70年代记忆电路被理论化并且成功地制作和研究了10多年。本研究有助于在物理上实现忆阻器用于存储器的两个优点和多级逻辑优点的多级加法器电路。
本文介绍了一种基于忆阻器的半加法电路,用于处理五进制逻辑的加法(减法)。第2节介绍了二进制编号系统,第3节讨论了主要思想并描述了所提出的体系结构,第4节说明了仿真结果。最后,第5节得出了结论。
2.五进制组编号系统
普通的二进制表示使用集合{0,1,2,3,4},并且平衡的五进制组使用不同的集合{2,1,0,1,2};所需的数字的位置是通过添加5v电源来表示。以类似的方式处理分数,然而,数字之后小数点将表示为1/5的幂。一个给定的平衡二进制数的例子是十进制数21,它可以用平衡的符号表示:111。在十进制数符号中该数字被解释为:1*52-1*51 1*50或25-5 1。
平衡的五进制组具有许多优点,如收敛性,它减少了乘法过程中的进位。此外,负符号使系统更加有效,在所有的算术运算中,不需要额外的符号。虽然实验其他的基数显示有趣的特点,但是在代数运算中,比如,消去二进制加法(减法)中的进(借)运算。这种特征不可能跟随传统的二进制表示布尔代数。二进制带符号数字表示使进位自由加法成为可能。
(63)10 (223)5 (63)10 (1222)5
(3)10 (003)5 (3)10 (012)5 (1)
(66)10 (231)5 (66)10 (1221)5
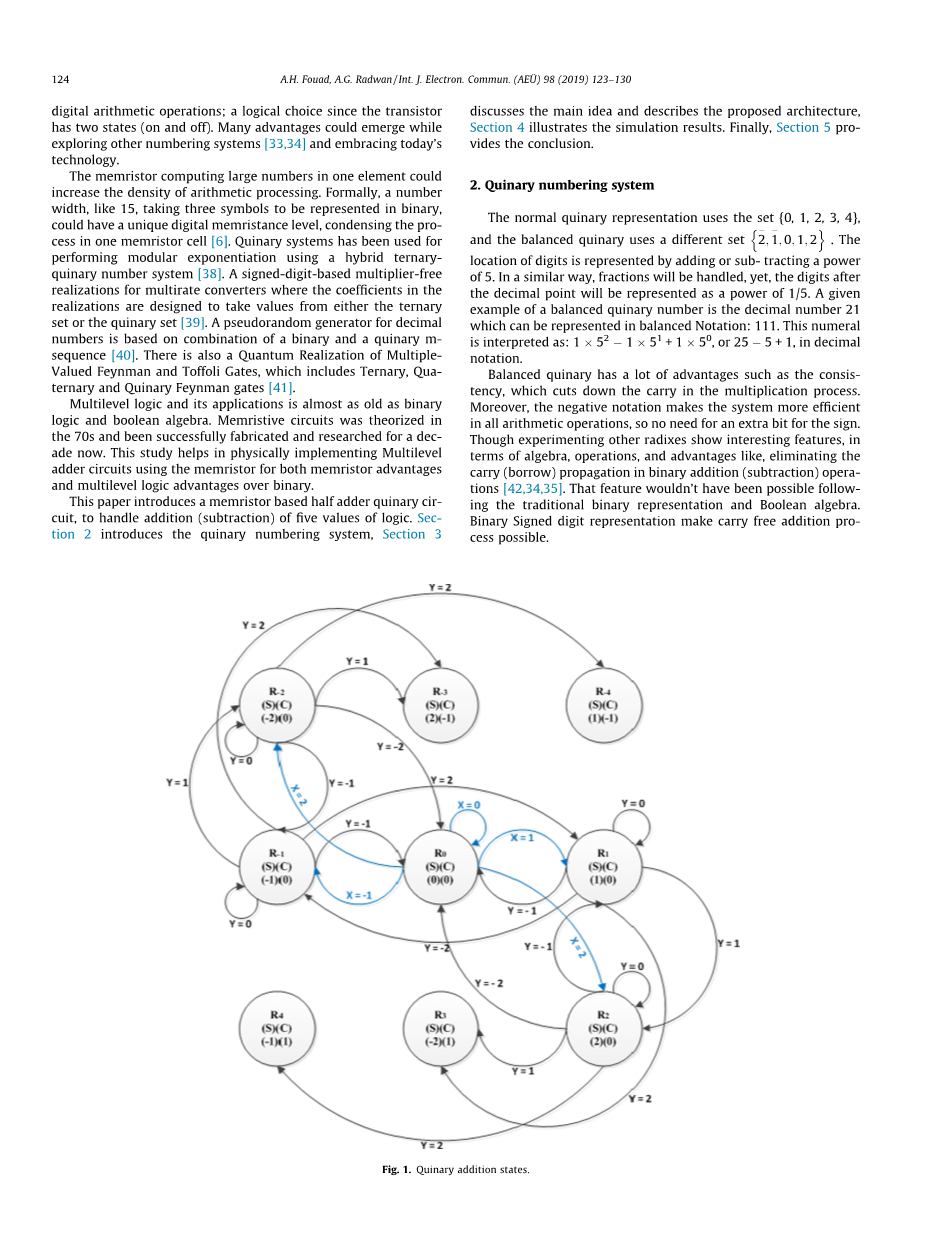
等式(1)显示了平衡五进制和不平衡五进制中小数相加和表示的区别。图1显示了平衡五进制加法的状态和进位。
二进制H不能执行和处理数据范围从2至2,可以在3位或4位二进制FA之间进行一个比较。五进制和MVL过程更多数据和数字在较少的位中。在2位QHA中,QHA保持9个不同数字(信息),而二进制FA仅在3中保持5个数字3位。因此,五进制组比二进制大,五进制组具有2.32x位比二进制信息更多的信息。二进制中的电路也变得很复杂并需要ALU区分负数和正数。而在平衡的五进制系统中具有固有地标志,无需额外电路即可执行(见表1)。
图1 五进制加法的状态
3.加法器体系结构
3.1忆阻量化
一项研究提出了一种硬件实现三电平加法器电路的设计。三进制,冗余二进制半加法器和无进位CSDC冗余二进制全加法器,其处理速度与操作器的长度无关。这些电路的推广可用于研究除二进制和三进制以外的不同进制。
以前,特定量的电流决定了电阻器根据其极性,从R到R的状态取决于R或R。此值将用|imax|表示。它是更改当前值从总电阻R的一半到R(或ROFF)的一半的记忆状态给定时间t。该值取决于当前极性,以及忆阻器模型是否为可逆的。
Rinitial=(Ron Roff)/2 (2)
电流Imax将确定逻辑电平值。所需的同一单元中的最高值或半加法器加法,对于单元来说是两个1s,而对于五进制组来说是两个2s。平衡的五进制组将替换不平衡的五进制集合{0,1,2,3,4}。逻辑1的值是通过下式计算的:将imax除以4(两个2s),因此逻辑2将加倍该值;负电平在幅度相同但方向相反的情况下,在五进制半加法器中,将添加两个2s,这将使得许多的记忆数量被量化。
图2平衡忆阻器的量化电平
记忆量被划分为九个区域。额外的级别是用于添加过程。其中的最高幅度二进制数字系统是2,增加将需要改进。图2显示了量化的记忆状态电平和每个级别的总和和进位。表2显示了真值表五进制的加法和它的等比的十进制值。
推导广义概念的关系单元将被量化为(2n-1)区域。在给定的脉冲宽度t.imax中,逻辑1将以imax/(n-1)表示这是是用于将忆阻器推离初始状态(一半忆阻)需要的值。Imax是用于将忆阻器从初始状态推入(一半忆阻)所需的值。
任何的较高逻辑都是是逻辑1的乘法。NEGA值具有相同的幅度和相反的方向,其中n是奇数基。可以通过更改(2n-1)至(2n 1)和(n-1)至(n)将规则改为偶数,。
图3中的流程图显示了有许多步骤需要控制添加忆阻器单元时的思考。复位保持为一个定义单元格的特征。以前,交换机和比较器用于区分状态。这些国家正在概括地说,在初始添加过程之后,修改了三个阶段。温度计A/D定义忆阻状态。公共级编码器将状态数字化成不同的值和电流极性。然后是另一个设计不同的编码器对于每个基。另一编码器在对于每个基的设计上是不同的。
编码器的输出分为两路:一个用于电流其极性的大小及其他极性,如表3所示,其中b0和b1为[10]选择正,[01]选择负极极性。MSB 0和1是当前多路复用器选择Ims的幅度。
图4 加法器脉冲序列
将图4中的图表分成前面提到的三个阶段:第一阶段:输入改变记忆状态的状态根据幅度,第二是读取阶段,这分为和的大小,然后是和进位。最后一步是将忆阻器重置为初始忆阻。下面的部分描述了如何通过修改冗余二进制加法器电路实现。
4、电路修正
建议的电路修改如图6所示。为了概括许多级别,模数转换器后面跟着一个编码器充分地将电平转换为二进制算术运算后的系统由忆阻器计算。从编码效率的角度来看,温度计代码效率更高,因为没有未使用的代码。
与以前相比,新架构使用的忆阻器更少,如图5所示。反面提议的电路,图6中的方法是使用一个忆阻器用于处理级别而不是三个或两个忆阻器。
相反,使用4位模拟-数字到编码器15级或9级,在后一种情况下浪费了6个代码,THER-MOM代码确保每个代码都类似于每个记忆状态,并且没有代码被浪费。但是,这些值需要被编码成能够表示向后波纹的数字,并且能够用于其它算术运算或用于创建n位加法器电路。同时将结果编码返回到其当前值,从表4中可以看出,零是两个中间位的异或结果。所需的水平的符号是一个正的符号和一个负的符号。电平的大小可以由3MSB确定。
要获得负电平中位的幅度,镜像3LSB位并反转它们以获得相同的值大小。或者旋转移位比特(N-1)次(n是位宽度),直到最高有效位是最低有效位,反之亦然。
图5 使用忆阻器单元的基于忆阻器的加法器电路
( a )三进制半加法器,( b )冗余二进制半加法器,( c )冗余二进制N位全加器
图6 拟议的电路修改
结果值由两个位控制的多路复用器馈送,在中间选择当前振幅。Gilbert单元控制电流方向。编码器输出幅度,忆阻状态为3位数字及其使用方向来自逻辑门。结果应该被馈送到另一个编码器,用于在所需的二进制基础上对数据进行编码,将其馈送到具有加权电流源的多路复用器中输入。其输出是Gilbert单元的输入。
来自第一级编码的结果在所有的基中是常见的,因为它将忆阻器级别编码为二进制,并阻止挖掘它的大小和方向因为所需的信息决定幅度的只是LSB,因为选择是在[逻辑1和逻辑2]2*1之间,Mux稍后可以用于确定电流,Im作为选择。
B0和B1开关类似地控制Gilbert单元在冗余二进制加法器中。图7显示了基于五进制的编码器电路。一个简单的电路还是五进制加法器,将具有波动进位作为三进制加法器半加法器电路。另一方面,五元包含更多信息比其更低的基添加。以及所需的编码真实性,表5对表进行了解释。
图7五进制编码器
其中I ms是电流多路复用器Select,B0和B1是电流极性的开关选择
必须在互惠忆阻器上实现;否则应该用一种新的方法来处理忆阻器的非互惠性。通用代码的结果用于测试在线性多巴漂移,忆阻器上施加数字电流值变化后施加不同电平的预期未改变结果(见表6和7 )。
5.实验结果
图8和图9的结果显示了忆阻的不同水平可以被馈送到A/D转换器。五个输入电流值代表{2,1,0,1,2}M(1)表示加法过程中忆阻状态的变化;例如状态R2,无论它是两个逻辑1的相加,还是逻辑0和逻辑2。输入以串行方式输入,之后施加读取信号,接着输入反相以再次重置忆阻器。
图8五进制电流输入及相应的记忆状态
图9 五进制电流输入对记忆体线性惠普实验室模型行为的影响
和Joglekar非线性模型
本节介绍了一种基于五状态(五进制基)的加法器结构的改进方法。记忆器密度降低了加工面积。由于以较少的位处理更多的信息,并且平衡表示法简化了减法过程,加法过程更有效,因为操作数本身包含负号数字。
未来的工作记忆状态移动较慢,因为它接近它的极限,因为掺杂的移动性。解决这个问题可能需要一个加权A/D转换器。不同的忆阻器 MOD-EL根据其功能和模型参数表现出不同的行为。对于所有的模型,互惠模型只能用于实现基于记忆单元的体系结构所需的功能。留下线性掺杂,非线性Joglekar,密歇根大学模型,和Prodromakis模型。
这些模型的数字波响应不同。当输入到记忆器的正弦波用方波代替时,频率相同。可以从每个模型中产生不同的状态,而不考虑非线性来区分每个模型,因此,应该相应地调整A/D的灵敏度,这也将决定可以达到的最大水平(最高基)。
简单的模型用于理论的概念,任何倒数模型都可以在相同的架构下使用,同时调整结论部分提到的A/D温度计。非线性模型和线性模型的记忆性比较表明,这些变化是可以适应的.下表显示了输入值的调整和某些模型A
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[20825],资料为PDF文档或Word文档,PDF文档可免费转换为Word


