
英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
利用改进的LMS自适应算法消除车辆噪声的解决方案
摘要——噪声消除系统的问题取决于其信源的具体特征。因此,在实施所设计的降噪方案之前,应该了解其每个噪声源。由于发出的噪音因过往车辆的类型而异,因此应自动调整方案。必须通过管理步长值来最小化延迟。
五种代表性的产生噪音的车辆(噪音来自:公共汽车,卡车,摩托车,柴油车和汽油车)总是随着过往车辆而变化。首先应用鲁棒LMS(最小均方)算法,然后修改LMS算法。
结果表明,采用自适应LMS算法修改的两个过程的LMS算法在车辆噪声消除中的应用是最简单最好的。
关键词:LMS(最小均方),延迟,步长,滤波器长度。
1.介绍
许多工作需要更多的注意力才能获得最佳结果。在许多大城市,噪音来自交通活动,工厂机器,建筑施工,道路建设等等。已经做了很多努力来减少噪音污染,但并非所有噪音污染都可以减少,换句话说,噪音不能100%消除。这是因为噪音特性总是快速变化。
消除噪音污染的方法之一是建造隔音材料或者带有能吸收噪音的材料的隔音房间。这种方式对于计算机实验室,法庭等非常有用。但是,并非全部建筑适用于这种防噪音系统。这是因为成本因素,并且也有一些噪音应该被听到。这种情况可以在位于主要街道附近的住宅区,学校和办公室中看到。这些设施需要高效的且有选择性的噪声控制设备。
车辆的噪声通常包含静态模式,换句话说,在很长一段时间内周期性地或随机地静止。静态模式中的噪音听起来令人不安,但仍然是大声的噪音和持续不断。
减少噪音污染的方法之一是制造一种噪音消除系统,该系统仍然可以维持被称为“助教”的信息信号。由于存在多种类型的车辆,因此应使用自适应消除过程以跟踪噪声类型。
1.1 目的
研究的目的地是:
1.观察许多来自车辆噪声信号的固定噪声信号。这意味着在光谱和统计两个方面都上满足车辆噪声信号的基本特征。
2.基于LMS自适应算法,采用最佳的车辆噪声消除算法。
1.2 总结
从各种车辆的噪声和许多调整方案,预计可以为独立打造完整的硬件和软件和实时自适应噪声消除提供机会。此外,它可以使科学家为另一种噪声开发相同的自适应方法和技术。
2.基础理论
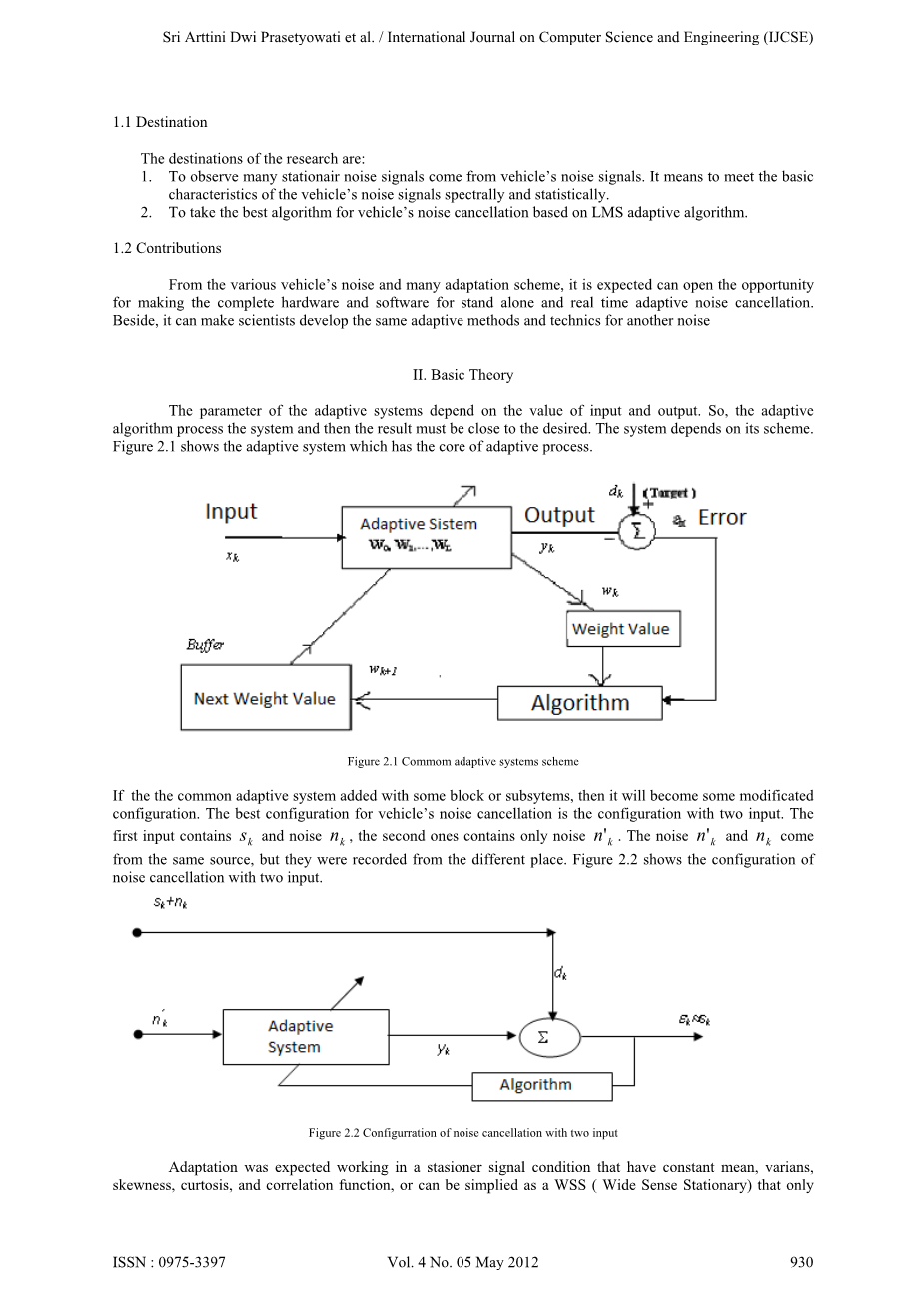
自适应系统的参数取决于输入和输出的值。因此,运用自适应算法处理系统,然后其结果必须接近所需。系统取决于其方案。如图2.1所示是自适应系统的主要自适应过程。
图2.1 总体自适应滤波方案
如果常见的自适应系统添加了一些模块或子系统,然后它将成为一种修改后的配置。 车辆噪声消除的最佳配置应该有两个输入。 第一个输入包含和噪声,第二个输入包含噪声。 噪声和来自同一个源,但它们是从不同的地方记录的。 图2.2显示了具有两个输入的噪声消除配置。
图2.2 具有两个输入的噪声消除配置
期望在具有恒定均值,变量,偏度,缩窄和相关函数的更平稳的信号条件下工作,或者可以简化为仅需要恒定均值和方差的WSS(广义平稳过程)。因此,算法必须符合该条件才能进行正确的适应。 LMS(最小均方)算法将作为主要参考。虽然具有长迭代,但LMS自适应算法运算简洁。
自适应LMS过程分析
导致权重向量的许多有用的自适应过程可以通过梯度方法找到误差性能曲面的最小值。 均方误差性能曲面的梯度指定为()或简称为,可以从以下公式得到:
(2.1)
求微分得到列向量:
对于和有:
(2.2)
假设R是非奇异的,这时最佳权重向量W *(有时称为维纳重量矢量)就成为:
(2.3)
该等式的含义是,如果xk和dk之间存在强互相关,则权重值将更大,并且如果xk具有弱自相关则将更小。
图(2.3)显示了自适应步骤的条件,权重值随着梯度值而变化。
图2.3 性能曲面
由于W * = R-1P,它可以归纳为牛顿迭代法:
(2.4)
在xk和dk未知的情况下,R不能用于算法,因此算法成为最速下降算法:
(2.5)
LMS算法由的偏导数形成,假设的平均值达到最小值。LMS算法是:
(2.6)
简单的LMS算法需要很长时间才能达到最佳值。
3.研究方法
本研究实现了具有两个输入的自适应噪声消除系统。 两个输入必须没有延迟。 记录的噪音来自五种车,包括柴油车,汽车,摩托车,公共汽车和卡车。 第一个输入记录在工作室中,第二个输入记录在噪声源附近。 该研究的目的是在不丢失信息的情况下取消噪音。
与人类语音信号相比,这项研究采用了互相关和自相关来精确测量车辆发动机噪声(如汽车,公共汽车,卡车,摩托车和柴油动力车辆)之间的任何相似性。由于公式W* = R-1P,相关性成为重要的过程。 自相关和互相关结果的拟合曲线可以帮助简化相关信号。
分析车辆噪声的FFT和频谱可以显示噪声频率的位置。 我们预计噪声的频率因信息而不同。相反,来自工作室内的噪声频率接近来自外部的噪声。 为了优化使其可以进行研究,将其与正弦信号进行比较,因为正弦信号是周期性的并且易于消除。
本研究中的重要案例是寻找三个变量的最佳值,L(滤波器长度),(步长)和延迟时间。在寻找车辆信号的最优值之前,先观察正弦的最佳值、锯齿等。
我们的研究将一直做到在信号保留的情况下,噪声被消除。 难点是噪声的频率和信息信号具有相同的范围,该条件导致了算法的修改。
4.结果结论
本研究实现了具有两个输入的自适应噪声消除系统。第一个输入是具有车辆噪声的信息信号,第二个输入是车辆噪声本身作为参考。噪音的记录来自柴油车,汽车,摩托车,公共汽车和卡车五辆车。第一个输入记录在工作室中,第二个输入记录在噪声源附近。该研究的目的是在不丢失信息的情况下取消噪音。
从之前的研究来看,一些研究人员只使用合成信号。甚至,其中一些只是分析某种算法的随机性。从这项研究中获取原始信号的研究尚未完成,特别是在印度尼西亚。
相关性是LMS算法成功实现噪声消除的条件,我们先从这里开始,然后从汽车,公共汽车,卡车,摩托车和柴油发动机驱动的车辆中获取几种车辆噪声信号的自相关,然后进行比较它们来自语音信号。
图4.1显示了互相关车辆噪声信号各自拟合曲线的前两个系数的散点图。
图4.1:互相关车辆噪声信号的相应拟合曲线的前两个系数的散点图。
图4.1清楚地显示了相关系数值与相似车辆类型的某些程度的聚类的扩散,而在远端是语音信号的聚类。这表明将语音信号与噪声很好的分离了。
图4.2显示了有和没有语音信号的车辆噪声信号的互相关。可以得出结论,在具有和不具有语音信号的车辆噪声信号的互相关之间没有显着差异。
图4.2车辆噪声信号与语音信号和非语音信号的互相关性
4.2 FFT分析
对车辆噪声信号的FFT分析表明,FFT结果的复数值与圆圈完全不同。 相反,正弦信号具有作为圆的复数值。 这意味着存在谐波周期性,因此正弦信号是易于消除的。 并且随机车辆的错误残留不再能够消除。 图4.3和4.4显示了总线信号的实数和想象值,以及正弦信号的实数和想象值。
图4.3 工作室内总线信号的实际值和想象值(1 - 5.000)
图4.4正弦信号的实数和想象值(49.000 - 50.000)。
4.3车辆噪声的分析光谱
几乎所有车辆的噪声信号都表明它们处于低频,而信息或语音信号处于低频和高频。 这种情况提供了可以从语音信号中消除噪声信号的机会。 图4.5显示了车辆噪声的频谱,图4.6显示了语音信号的频谱。
图4.5 来自工作室的车辆噪声信号频谱,采样频率为44100 Hz
图4.6 采样频率为44100 Hz的语音信号频谱
相关性,FFT和频谱分析表明语音信号可能与车辆的噪声不相关。因此,有了这种成功的信心,这项研究将继续寻找用于LMS算法的正确参数值。
研究寻找从简单信号开始的参数值,有正弦,锯齿和方波信号。在现实中,正弦信号可以通过LMS算法快速且完美地消除,但是由于自适应过程在寻找正确的步长值时遇到困难,因此车辆的信号更难以被消除。
4.4在自适应LMS FIR预测中找到和
这种自适应LMS预测车辆的噪声信号是在所需输入等于参考值的情况下完成的。 对于所有k次迭代,结果必须显示误差接近于零。但是,在现实中,误差接近修复间隔并在该间隔中进行振荡。 这是因为误差仍然存在计算误差,并且从统计性和相关性表明误差残留接近高斯白噪声。
4.5在车辆噪声上应用LMS自适应
为了找到,L和正确的延迟样本,对车辆噪声信号自适应的非预测LMS进行得很复杂。有很多方法可以找到,L和正确的延迟样本,有重叠而不是移动平均,MSE,某些延迟样本的最大权重。从该研究中可以发现,= 0,001,L = 150,正确的延迟样本是200。但是,该结果仍然有困扰的噪音。因此,噪音消除尚未成功。
最后,经过长期研究,对LMS自适应算法进行了修改,即LMS自适应算法采用两个过程(图4.7)。第一个过程,所需的输入是在房间内记录的车辆噪音,参考是车辆在房间外记录的噪音。在第二个过程中,所需输入是第一个过程的期望值和参考值之和。第二个过程的参考是第一个过程的输出。
图4.7 具有两个自适应过程的LMS
在找到最佳值时,LMS自适应过程以两个过程使用MSE作为参考。 LMS中所有车辆噪声的步长自适应的两个过程具有相同的值,即0.001。 L和延迟最佳值为230和100个样本。
以上结论是自适应LMS算法的两个过程,即如果它应用于车辆的噪声消除,自适应LMS算法的修改是最简单和最好的。
考虑到如果所有噪声信号都经过低通滤波,自适应LMS噪声消除变得更加完美,那么使用适当的硬件可以选择最佳L(如果可能,L的值可以大于470),这样 车辆的噪音消除效果很好。 除了两个Matlab程序,在80000个样本中取消车辆噪声信号所需的时间是91.091.000秒或大约15分钟。 如果我们知道车辆噪声信号的重量值,我们需要消除噪声的时间更短,可以清楚地看到。 在上述过程中,我们可以节省时间,直到13.5分钟或90%。 我们可以从上面的事实中用适当的硬件得出结论并知道每个车辆的噪声信号的权重,可以实时实现自适应噪声消除。
4.6结论
从以上解释的研究结果可以得出结论:
1.关于相关性,FFT和频谱的分析表明很有可能将语音信号与噪声分离,尽管找到适当的延迟,滤波器长度和步长存在许多困难。
2.利用自适应LMS算法可以消除各种类型车辆噪声引起的噪声,该算法在L = 230,= 0,001的两个过程级别进行了修改,在线性组合器中采用最简单的结构延迟了100个样本。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[19801],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


