检验水文系列单调趋势的Mann-Kendall检验和Spearman秩次相关法的检验功效外文翻译资料

 2022-12-06 15:57:34

英语原文共 18 页，剩余内容已隐藏，支付完成后下载完整资料

检验水文系列单调趋势的Mann-Kendall检验和Spearman秩次相关法的检验功效

摘要：在许多水文研究中，两个非参数基于秩的统计检验即Mann-Kendall检验和Spearman秩次相关法，被用来检测时间序列数据中的单调趋势。然而，这些检验的功效还没有被很好的记录。本次研究调查了蒙特卡罗模拟检验的功效。模拟结果表明，它们的功效取决于预先指定的能量水平，趋势大小，样本大小和时间序列内的变化量。也就是说，趋势变化的绝对值越大，检验的功效越大;随着样本量的增加，检验变得更可信;并且随着变化量在时间序列内增加，检验的功效降低。当趋势存在时，功效还取决于时间序列的分布类型和偏斜度。模拟结果还表明，这两个检验在检测趋势方面具有相似的功效，同时在实践中难以区分。这两项检验用于评估加拿大安大略省20个原始盆地的年最大日流量数据趋势的显著性。结果表明，通过这些不同测试计算的P值几乎相同。通过二项分布，在0.05的显著性水平评价了连续显著的下降趋势。结果表明，较高数量的网站显示比预期单独检验来说其下降趋势的证据更明显。

关键词：Mann-Kendall检验; Spearman秩次相关法; 非参数检验; 趋势分析; 检验功效; 统计水文学

  1. 简介

基于秩的非参数Mann-Kendall（MK）统计检验（Mann，1945; Kendall，1975）已被广泛用于评估水文气象时间序列的趋势的显著性，例如水质，流量，温度，沉淀。使用非参数统计测试的主要原因是与参数统计测试相比，非参数测试被认为更适合非正态分布数据和截尾数据，这在水文气象时间序列中经常遇到。在非参数测试中仍然需要时间序列的串行独立性。使用MK测试来检测水文和水文气象时间序列趋势的例子包括Steele等人（1974），Hirsch等人（1982），Hirsch和Slack（1984），Crawford 等人（1983），van Belle和Hughes（1984），Cailas等人（1986），Hipel等人（1988），Taylor和Loftis（1989），Demaree和Nicolis（1990），Gan（1998），Zetterqvist（1991），Mcleod等人（1991），Chiew和McMahon（1993），Yu 等人（1993），Lettenmaier等人（1994），Burn（1994），Yulianti和Burn（1998），Lins和Slack（1999），Douglas等人（2000），Zhang 等人（2000,2001），Yue等人（2002）等的作品。尽管该检验被广泛使用，领域当前状态还是在各种情况下用于检测趋势的MK检验的功效还相当不完善。

Spearman秩次相关法（SR）是另一个基于秩的非参数统计检验，也可用于检测时间序列中的单调趋势（Lehmann，1975; Sneyers，1990）。然而，由于Hirsch等人的论文的发表（1982），MK测试被普遍用于评估水文气象时间序列趋势。种种原因下，SR检验很少用于水文气象趋势分析。使用SR检验的有限实例包括Lettenmaier（1976），El-Shaarawi等人（1983），Pilon e等人（1985），McLeod 等人（1991），以及Hipel和McLeod（1994）。这两种方法之间的这种不成比例的应用可能导致一个误解，即MK检验优于检验水文气象时间序列趋势的SR检验。

本研究的目的是（I）记录MK检验和SR检验的能力以检测趋势，以及样本大小和样本变化对检验功效的影响; （II）探讨检验功效对分布类型的样本数据的敏感性; （III）比较MK和SR检验的功效; 和（IV）讨论统计显著性和实际意义之间的差异。这两个检验也用于检验加拿大安大略省20个原始河流流域的连续独立的年最大日流量数据的趋势。

  1. 检验功效（power）计算

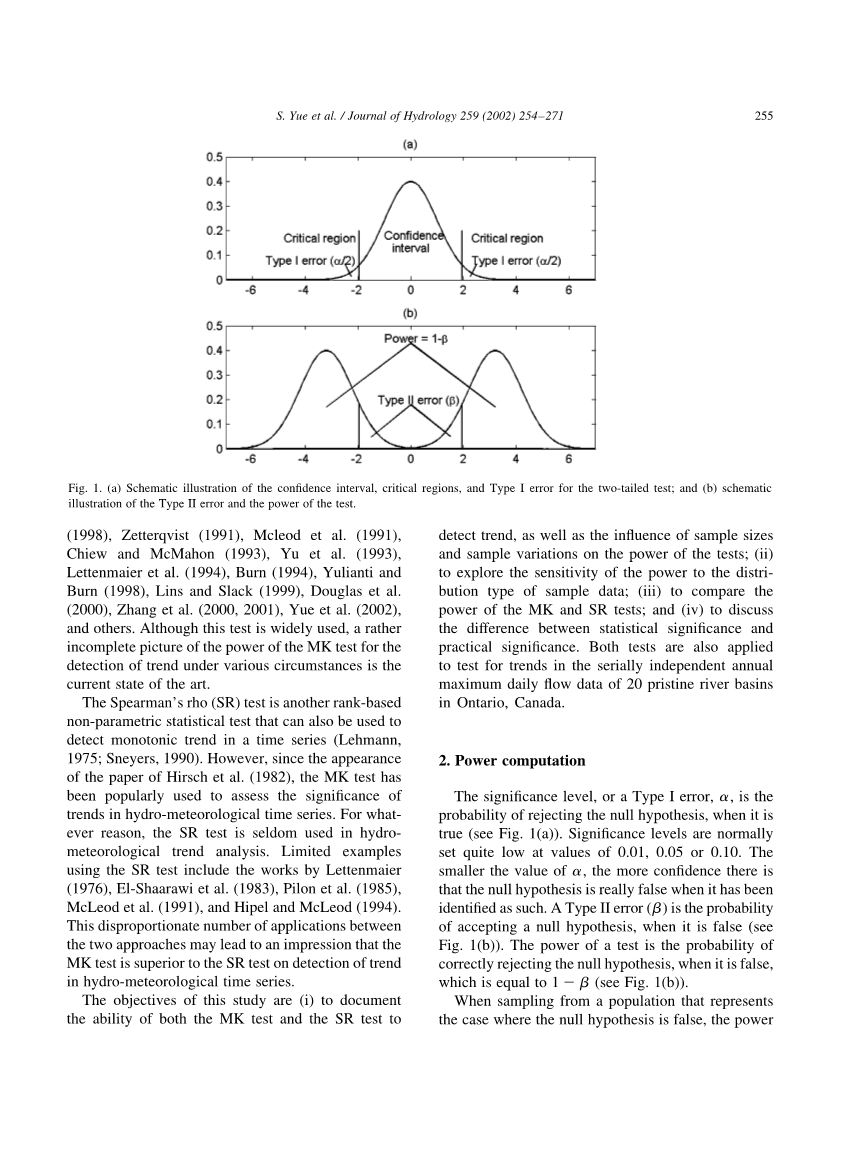
显著性水平或第一类错误（alpha;）是当其为真时拒绝原假设的概率（参见图1（a））。显著性水平通常设置为相当低的值为0.01,0.05或0.10。 alpha;的值越小，当假设已经被确认为零时，原假设真的是假的就越有信心。第二类错误（beta;）是当假设为假时接受原假设的概率（参见图1（b））。检验的功效是当假设为假时正确拒绝原假设的概率，其等于1-beta;（见图1（b））。

当从表示原假设为假的情况的群体采样时，可以通过下式估计功效

图1（a）双尾试验的置信区间，临界区，第I类错误示意图；（b）检验的power示意图

(1)

其中N是模拟实验的总数和Nrej是落在在临界区实验次数（参照图1的（b））。 MK和SR检验的统计数据见附录A.MK统计量（S）的定义域可以近似由下式给出

或 (2)

其中Zalpha;/2和Z1-alpha;/2分别是标准正态分布的alpha;/2和1-alpha;/2的置信度; V（S）是MK统计量S的样本方差（见附录A）。对于SR检验，临界区可以通过类似于公式（2）中的近似不等式给出。（2）式其中V（S）由SR统计量D的方差V（D）代替（见附录A）。

3.检测趋势的MK检验的功效

通过蒙特卡罗模拟检验MK检验的功效。实验为每个样本大小生成2000个独立的正态分布时间序列（Rt）。每个样本n=10(10)100,平均值E（Rt）=1.0及不同的方差V(Rt)=(1.0*i)2其中i=1(1)10。相应的标准偏差（SD(Rt)）和变异系数(CV=SD(Rt)/E(Rt))为0.1（0.1）1。

将所选的特定线性趋势情景（Tt=bt; b=-0.01（0.002）0.01, t=0,1,2，hellip;，n）叠加到每个所生成的系列上。

图2总结了样本大小n=50，变异系数CV=0.5下的功效、显著性水平、趋势大小或斜率之间的关系。其他样本大小也适应类似的模式。选择50的样本大小仅仅是为了说明目的。对于固定显著性水平alpha;=0.002,0.005，0.01，0.025（0.025）0.20，检验的功效的趋势是绝对斜率的递增函数。当趋势的斜率一定时，增加显著性水平也增加了功效。

图3描绘了给定显著性水平为0.05和变异系数CV=10的功效，趋势斜率和样本大小之间的关系。检验的功效是绝对斜率和样本大小的递增函数。换句话说，随着样本大小增加，检验的功效增加，趋势存在越能被发现。

图2power—斜率—显著性水平曲线（n=50,CV=0.5）

图3power—斜率—样本大小曲线（alpha;=0.05,CV=0.5）

图4总结了样本大小n=50，变异系数CV=0.05下的功效、显著性水平、趋势大小或斜率之间的关系。显然，对于固定斜率，检验的功效是时间序列的变化系数的递减函数。也就是说，随着时间序列内的变化量增加，检验的功效降低，这意味着更难以检测趋势的存在。

图5power—变异系数—样本大小曲线（alpha;=0.05,b=0.005）

图4power—变异系数—斜率曲线（alpha;=0.05,n=50）

本质上，一系列内的变化掩盖了趋势的存在。近似地，图5给出了趋势b=0.005,显著性水平为0.05下的功效、样本大小和变异系数之间的关系.

根据这个分析，我们可以在预先指定的显著性水平上确定最低要求的样本量来检测预先指定的人口趋势。这种分析还可以用于为水文气象观测网络设计提供信息，网上现有的一项应用即监测可能由于温室气体浓度的增加而引起的潜在逐步变化（Slack和Landwehr，1992;《加拿大环境》，1998年）。

4.非正态分布趋势下的MK检验的功效

图7具有不同正偏度（gamma;）的P3-分布系列的power-斜率曲线

图6不同分布类型的检验power

在第三节中所提到的MK检验的功效的说明是基于正态分布下的。然而，水文气象时间序列往往被扭曲，很少遵循正态分布。本节进一步研究了MK检验检测非正态分布时间序列趋势的能力。水文中的一些常用分布类型，即极值分布（EV1，EV2和EV3），Pearson 3型分布（P3）和对数正态分布类型，常被用于检测检验的功效。对于这些分布类型的系列生成，读者可以参考Stedinger等人的研究。（1993）

与第3节类似，生成2000个时间序列，样本量为50，平均值为1.0，标准偏差为0.5，并生成上述每种分布类型。具有不同分布类型的功效 - 坡度曲线如图6所示。在没有趋势的情况下，检验的功效对于不同的分布类型保持相同，并且等于预先指定的0.05的显著性水平。这表明MK检验统计量的零分布对时间序列的分布类型不敏感。然而，在存在一些趋势的情况下，检验的功效对于不同的分布类型是明显不同的。这不是因为样本较小或模拟样本较少。EV3具有最高功效，而对数正态分布具有最低功效。这个结果表明，当趋势确实存在时，MK检验的能力也取决于分布类型，这与MK检验是基于等级且是无分布的一般想法相反。

为了说明检验的功效也取决于样本数据遵循的概率分布的形状参数，具有正偏态的P3型分布的时间序列的功效如图7所示。具有EV3分布式的功效如图8所示。图7和8表明，检验的功效也受分布类型的形状参数影响。Kingman和Gary（1994），Levy和McCuen（2000）也观察到了这一点。

图8具有不同形状参数（k）的EV3-分布式系列的power-斜率曲线

如前所述，功效的增减可能影响对许多地点的显著性结果的整体解释，称为场意义（Livezey和Chen，1983）。在趋势检测研究的趋势重要性评估中，人们在水文循环内对各种变量进行推论时，情况尤其如此（Lettenmaier等人，1994; Zhang 等人，2001）即使两个变量如降水和流量可能具有类似的趋势分量，测试统计量辨别趋势的存在的能力仍将受到站点的统计属性（如偏度）的影响。这些属性将根据要分析的变量而变化，这使得趋势模式跟变量相比比预期更复杂。这些属性也会影响站点意义的整体评估，因为它仅反映了个别站点。让我们来举个例子说明一下，具有100个站点的两个网络各自具有相同的趋势大小（b = 0.005），如果第一网络站点是正态分布，并且第二网络是P3分布（gamma;= 09），则我们可以预期基于结果的检测率大约加倍，如图7所示。检测率的这种增加可能影响趋势证据的总结。实质上，当趋势存在时，检验的功效受站点特性的影响显著。

  1. MK和SR检验的功效的比较

其他作者也比较了MK和SR非参数检验（例如Daniel，1978）。研究发现，其中一个仅有很少的基础因为比另一个所用太少。但是，Daniel（1978）在比较MK和SR测试统计数据时提到了几个关注点。他指出，S的分布比D更快地接近正态分布;S提供总体参数的无偏估计，而D没有，因此，S是更合理的。

按照与前述部分相同的方法，同时检查功效，斜率，样品大小和SR测试的变化系数之间的关系。对于两种方法获得结果非常相似，并且为了简洁起见，结果未在论文中报告。

进行两个检验的功效的比较，并在本文中给出。对于正态分布的随机变量，样本量n = 50和100，CV = 0.5和alpha;= 0.05的功效 - 斜率关系显示在图9（a）和（b）。对于n = 50和100，b = 0.005和alpha;= 0.05的功效 - CV关系如图10（a）和（b）所示。图11出示了对于CV = 0.5，b = 0.005; alpha;= 0.05的各种样本大小的两个检验的功效。可以看出，对于检测设计的线性趋势，两个测试具有几乎相同的功效。

图9比较不同斜率下MK检验的power和Spearman秩次相关法power其中CV = 0.5,alpha;= 0.05,（a）n = 50;(b)n=100

对于非正态分布的时间序列，以50和100的样本大小为例，具有1.5的偏斜系数的P3分布的两个检验的功效在图12(a)、（b）中示出,针对负偏度为1.5进行后发现，结果也非常类似，如图12所示。同时对其他分布类型的两个检验的功效进行比较。结果表明，这两个检验也具有类似的用于检测高偏斜度时间序列趋势的功效。其他样本容量下的功效也很类似，如图11所示。

图10比较不同变异系数下MK检验的power和Spearman秩次相关法power其中b=0.005,alpha;= 0.05,（a）n = 50;(b)n=100

  1. 案例研究

本节应用这两个检验方法来评估位于加拿大安大略省的20个原始河流流域的年最大日流量数据趋势的显著性。这些盆地的日平均流量数据记录在加拿大环境局（1999年）的HYDAT CD-ROM中。这些盆地的排水面积，记录长度，平均值，变异系数，偏度系数和年最大流量的峰度系数分别列于表1第（3）-（8）栏。按它们数字标识的站的空间分布如图13所示。对于正态分布的随机系列，其偏度和峭度应分别等于0和3。从表1中显而易见，数据是正偏态的，并且很可能很难由正态分布描述。

图11比较不同样本大小下MK检验的power和Spearman秩次相关法power其中CV = 0.5,alpha;= 0.05,b=0.005。

显著性水平为0.10的每年最大日流量的双尾试验下,滞后1序列相关系数（r1）及其置信区间的上限和下限由表1第（9）-（11）栏列出。（参见Anderson，

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[25113]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章