关于雾滴谱的研究外文翻译资料

 2022-12-12 17:19:50

英语原文共 6 页，剩余内容已隐藏，支付完成后下载完整资料

关于雾滴谱的研究

P. BARONTI AND S. ELZWEIG

摘要：本文讨论了导致静止雾中观察到的液滴光谱分布的可能现象，并深入研究了这些分布与所期望的过饱和和湍流条件之间的关系。它假设凝结核从上方进入雾层，并由层内存在的超饱和状态激活。液滴在过饱和的环境中生长，在重力作用下下降。这种系统的描述中，所有大小的粒子都需要一个统计公式，正如喷雾方程所提供的那样。当液滴扩散被忽视时，喷雾方程的解是不现实的。本文将液滴扩散的喷雾方程与必要的边界和初始条件结合起来，给出了液滴大小和密度的实际定量估计。

1. 介绍

一个很有趣并且很有物理意义的问题是在雾中观察到的液滴光谱分布和液滴数密度的冷凝水汽产生的过程。这个问题有点类似于云计算的形成（Fletcher，1966），以及最近的一次研究（Kovets，1969）。然而，在云的情况下，我们研究了一种含有激活核的上升气流的竞争过程，通常不考虑在液滴形成过程中对空间的依赖。在雾霾的情况下，后者是重要的，因为在雾层中，原子核的活化作用是在雾中开始的，而在雾层中，液滴的生长仍在继续，因此，在一般情况下，液滴光谱和数量密度依赖于高度。

在本次研究中，我们的注意力仅限于静止的一维雾，即已经形成的一种自我维持并且仅考虑垂直尺度的雾。我们还假设雾层的温度和湿度是已知的，因此可以通过设想以下物理过程来研究液滴形成和生长。各种尺寸的核的群体以一定的沉降速度进入雾顶。一些核根据过饱和的主要条件被激活。 细胞核在过饱和环境中开始生长成液滴大小，并向地面下降。同时湍流扩散趋向于在液滴生长时均匀地分布液滴，预期的结果是在任何雾高处具有相当宽的液滴光谱分布。

这一过程的形成阶段中，有许多大小的粒子在一个动荡的介质中生长和扩散，这需要一个统计描述。这种描述是由喷雾方程提供的。我们对两种情况进行了分析，首先考虑零滴扩散的情况。结果表明，不现实的光谱分布和液滴密度是由这个假设引起的，通过将现象学湍流扩散定律引入到喷雾方程中，分析了液滴扩散。不仅是实际的光谱分布，而且在雾层中所选的超饱和度和湍流水平的选取值，还揭示了在雾顶附近的湍流分布中所扮演的角色。

只有将现有的分析与辐射分析相结合，使辐射穿透到雾层中，才能确定该层中过饱和的实际分布。然而，喷雾方程的目前解决方案建立了观察到的液滴谱与过饱和和湍流扩散的预期条件之间的关系。

2. 凝结核的分布

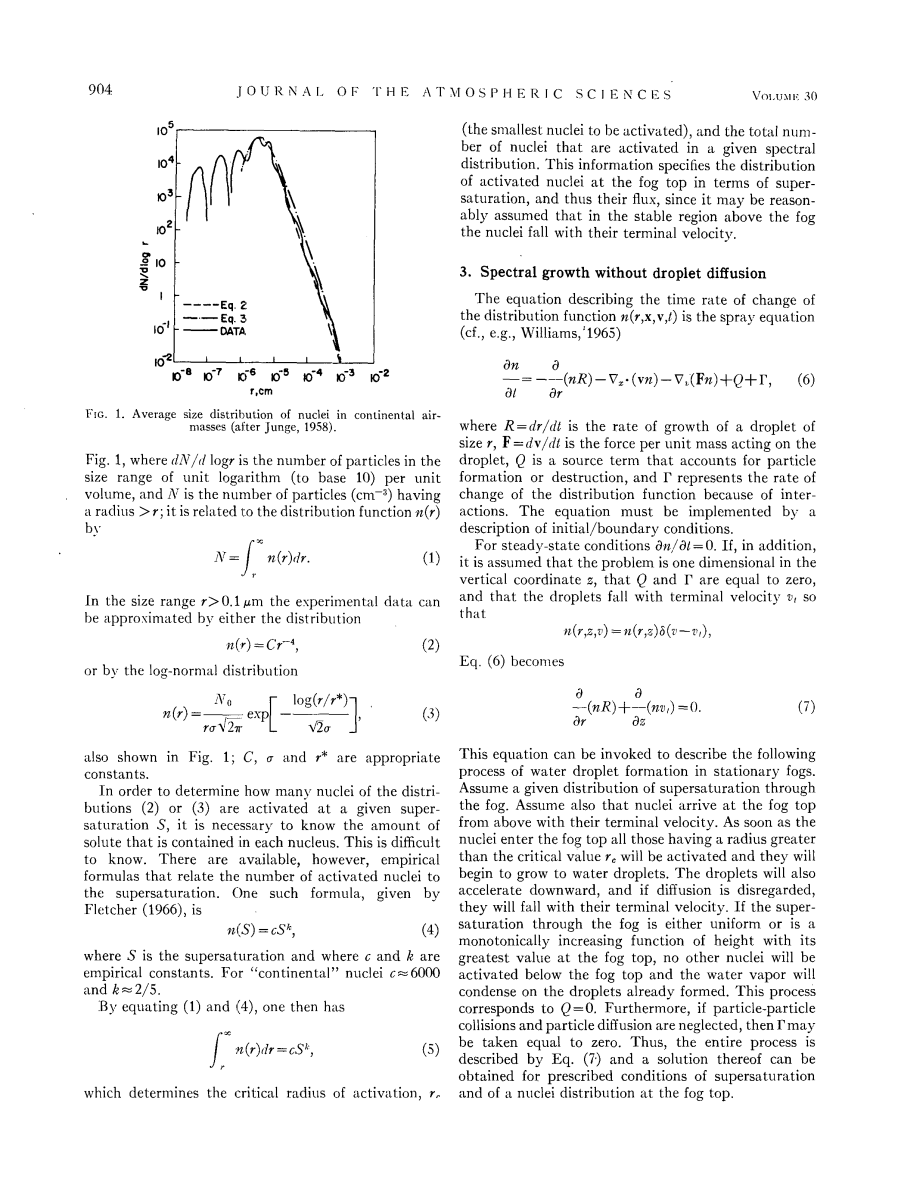
对于该问题的边界条件的规范，首先需要确定进入雾顶的被激活的原子核的通量。从Junge(1958)的研究中可以看出，凝结核在大陆区域的空气质量分布中，可以用对数正态分布的叠加来表示。一个典型的分布如图1所示

是指单位对数的单位对数的大小范围内的粒子数(以10为底的单位体积)，而N则是半径gt;r的粒子数(cm-3)；它与分布函数n(r)有关：

在r gt; 0.1mu;m的尺寸范围里，实验数据可以被任意一个分布近似

或者呈对数正态分布。

为了确定在给定的超饱和状态下，有多少个分布(2)或(3)的原子核被激活，有必要知道每个原子核中包含的溶质的量。这很困难，然而有一些经验公式将激活原子核的数量与过饱和联系起来。一个这样的公式，由Fletcher（1966）给出：

S是过饱和度，c和k是经验常数。“大陆”核casymp;6000，kasymp;2/5。

通过平衡(1)和(4)，就有了

这决定了激活的临界半径,r(被激活的最小的原子核)，以及在给定的光谱分布中被激活的原子核的总数。这个信息指定了在雾中处于饱和状态下的被激活的原子核的分布，因此它们的通量，因为可以合理地假设在大雾上方的稳定区域，原子核以它们的末端速度下落。

3. 无雾滴扩散的谱生长

描述分布函数n(r,x,v,t)的时间变化率的方程是喷雾方程(Williams,1965)

R = dr / dt是一个小液滴的生长速率，F = dv / dt是每单位质量的单位质量，Q是一个源项，用来描述粒子的形成或破坏，而Gamma;代表了由于相互作用，分布函数的变化速率。方程必须通过对初始/边界条件的描述来实现。

对稳态条件part;n/ part;t= 0。如果另外假设问题是在垂直坐标上的一个维度，那Q和Gamma;等于零，这些液滴落在末速度v上，所以

方程（6）变为

这个方程可以用来描述静止雾中水滴形成的过程。假设在雾中有一个特定的过饱和分布，原子核以其终端速度从上面到达雾的顶部，一旦原子核进入雾中，所有半径大于临界值r的半径将被激活，它们将开始成长为水滴。液滴也会向下加速，如果不考虑扩散，它们就会以终端速度下降。如果在雾中是均匀的，或者是一个单调递增的高度函数，在雾的顶部有最大的值，没有其他的原子核会在雾的顶部被激活，水蒸气会凝结在已经形成的液滴上。这个过程对应于Q = 0。此外，如果粒子粒子碰撞和粒子扩散被忽略，那么Gamma;可能会被取为零。因此，整个过程是由方程（7）描述的，并且可以通过在雾顶的指定条件和一个原子核分布中得到一个解决方案。

为了简单起见，我们可以考虑这样一个例子：S与高度是常数，R = a / r，与S成比例(这等价于忽略曲率，以及溶质对液滴增长的影响)。然后，通过设置Vt= br2，b是比例常数，方程（7）变成(用z坐标从雾中向下测量)：

zasymp; 0的边界条件(对应于雾的顶部)是

n0(r)是雾顶激活核的分布。方程(8)通过标准的特征方法得到的结果为

z的半径r与它的初始值ri有关，在z = 0处，通过

得到结果

上述解决方案的扩展，即为可变的过饱和条件。,a=a(S)=a(z),是直接的：只需要替换产品az替换为积分。

由方程(2)得出的初始激活核分布，n(rl0)=n0=C/r4，a为常数，则有

因此，对于总液滴数N(cm -3)，

r =[rc4 (4a/b)z]1/4以及4az/b ≫ rc4有渐近值

可以很容易地得到相应的解，以得到一个对数正态初始分布的原子核。当最初的原子核都是同一半径r0且r0 ≫rc的时候，就可以保证粒子的生长，n(r,0)=N0delta;(r-r0)。后一种情况则有

这显然是方程的解

通过设n(r,z)=N(z)delta;(r-r0)由方程（7）得出。

现在可以讨论上述解决方案的相关特性。从最简单的初始核开始，所有相同的大小，方程（11）告诉我们，如果初始半径r0的原子核变成半径r = l0r0的液滴，液滴的数目(cm-3)被降低了100倍。例如，如果最初的总体由1000核cm-3的0.5mu;m半径组成，当液滴到达5mu;m大小时，只有10个液滴cm-3的数量会产生。这个结果通过考虑解决方案(9)和(10)为初始分布的活化核n0(r)= 4.35X10-12 / r4，rc= 0.1体育馆而强调，因此，N = 1500cm-3对应一个典型的1%的过饱和度和b=1.3times;106的值。图2中显示了分布函数的快速陡化，即使对于很小的z = 4times;10-4 cm，对应于4az / b = 10-17cm4的值，如图2所示。对于值z=0.4cm，则有值4az/b=10-14cm4，分布函数几乎是垂直的，所有的水滴获得大约3mu;m的尺寸。相应的液滴数密度只有约4 cm-3。

当它们通过过饱和环境时，液滴数密度变得非常小。这适用于任何值的参数az（或者），也就是说，任何过饱和区组合的过度饱度S和深度z会导致粒子半径的尺度在5mu;m。这对于从雾顶到地面的一个过度饱和分布也是一样，从而创造了新的核被激活和水滴形成的较低高度的可能性。这种情况下，方程（7）被等同于一个源项Q，它是通过与新原子核的激活速率相关的过饱和成熟性的变化而获得的。结果表明，即使是在这种情况下，也不可能恢复粒子数密度的实际值，显然，上述的液滴形成机制必须加以修正。

4. 雾滴谱的生长与液滴扩散

如果雾滴落在湍流或者混合的区域，湍流扩散将趋向均匀分布在湍流区域的液滴浓度。这种扩散过程与引力效应竞争，降低较大液滴的沉降速度，并提供一种将小水滴传输到下层的机制。预期的净结果是在任何雾高度的液滴的光谱分布范围更广。

通过对重力的联合效应和谱分布扩散速率变化的分析，我们仍然可以通过整合方程（6）使用框架内的喷雾方程，所有的速度通过识别和空间平均速度v = vt -(D / n)part;n /part;z，vt为终端速度，D为飞沫扩散系数，(D / n)part;n /part;z为扩散速度。通过保留条件part;n /part;z = 0,Q = 0,Gamma;= 0和R = a / r，喷雾方程采用形式

由于z轴从地面往上测量，所以vt=-br2.

方程(12)必须通过对扩散系数D的适当描述和适当边界条件的规范来实现。如报告（Fleagle，1952）在雾层中存在的不稳定的分层条件导致了一个本质上动荡的区域，除了地面附近和顶部附近的薄层，湍流可能迅速衰减。例如，在Soo(1967)之后，可以合理地假设液滴的湍流扩散率小于，比如说，2 mu;m等于周围流体颗粒的大小。较大的水滴有较低的扩散性，但由于这种尺寸的液滴很少出现在雾中，所以可能认为所有的液滴大小都是有效的。另一方面，在靠近地面或接近雾顶的地方，D应该接近与层流或布朗运动有关的较小的值。

边界条件可以指定如下。首先需要指出的是，方程(12)是一个与r变量替换时间变量的热传导型的抛物型偏微分方程。因此，我们必须寻求在时间依赖的热传导问题中遇到的类型的初始和边界条件。通过注意液滴通量的守恒要求，可以得到r的初始条件

其中rrsquo;是系统中最小的液滴的半径，随后由方程（12）

对于r gt; 0，得出

对于r =0

方程(13a)假设如果r = rc(激活原子核的临界半径)，在雾中不会出现小滴。这对于任何实际的目的都是正确的，因为所有非活性的原子核都有半径r lt; rc，可以出现在雾层中，因为它们不参与到液滴形成的过程中。方程(13b)在任何雾高的情况下，如果在r = 0的整个核范围内，在rge; 0时，液滴分布函数的斜率是零。

边界条件是容易得到的。雾滴粘附在地面上的条件需要

在雾的顶部(z = H)粒子通量守恒要求

k（r，H）是进入雾层的活性核的通量。方程(12)通过一个基于z方向的中心差分公式和在r方向上行进的显式方案来数值解。下面给出了典型的解决方案。

5. 典型的结果与讨论

通过假设雾高100英尺、恒定的0.25%的饱和度，以及在雾层中持续的湍流扩散系数为0.215times;104，获得了方程（12）第一个解决方案。根据方程(2)，在雾的顶部，被激活的原子核的通量被要求等于4.35times;10 -12br-2[cm-3sec-1]，与b = 1.3times;l06 cm-1sec-1和rge;rc= 0.1mu;m。图3显示了三个雾层的结果光谱分布。让人震惊的结果是,相应的液滴数密度万是不切实际的小，仅有10-1cm-3的数量级。结果是产生了紊流扩散系数的假设常数。实际上，在顶部的液滴的守恒和从本质上等于零的D从本质上等于零的不连续性，就在下面的大雾上方，需要在雾顶下立即失去数密度。当非生长粒子的分布进入均匀的紊流区域时，也会发生类似的情况。

更现实的情况是可变湍流，因此，在雾层中有一个可变的液滴扩散系数。具体来说，图4中所示的分布，以及两个值的过饱和度(0.125和25%)都被选中。图5和图6给出了三个雾层的分布函数。数字密度N，平均半径r，以及与图5的分布相对应的液体水含量LWC如下所示

这些结果表明了雾滴谱生长过程的主要特征。实际上，相关参数的大小顺序和特征趋势。如在雾中观察到，数密度的减小、平均半径的增加和液态水含量随高度的降低等。

通过对图5和6的比较，相应的，减少液滴平均半径和液态水的含量，就能使光谱分布向左边的方向变化。然而，相关的观察结果与在雾顶的湍流所扮演的角色有关。连续不断增加的湍流，从零到雾顶到其充分发展的数值，在雾中较短的距离，不仅在物理上是现实的，而且在液滴数密度的情况下，会使被激活的核平稳地增长到液滴大小

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[27155]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章