金属泡沫夹芯圆柱壳在脉冲作用下的近似理论分析外文翻译资料

 2022-07-27 16:37:41

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

金属泡沫夹芯圆柱壳在脉冲作用下的近似理论分析

Lin Jing，Zhihua Wang，Longmao Zhao

摘要

采用简化理论分析方法，预测了泡沫铝夹芯圆柱壳在空气爆炸载荷作用下的动力响应。在这个解析解中，该夹层壳的整体响应分为三个阶段，与现有的夹层壳的三阶段理论框架相似。在第一阶段，假定冲击脉冲只传递前面板的速度。在第二阶段，金属泡沫芯大约成渐进压缩模式，而背面板仍然静止。最后阶段采用了传统的基于能量耗散率平衡的单壳体理论的方法；最大背面板中心点挠度和响应时间的“上”“下”临界值是通过全面限制和记录屈服轨迹获得。通过理论预测和实验结果发现，可以得出圆柱壳最大背面板中心点的偏转的一个合理结论。建议性的理论考虑对指导工程应用中的蜂窝金属夹层结构在空气爆炸载荷下的影响是十分重要的。

关键词： 泡沫， 冲击行为， 解析模型 ，夹层壳

1 引言

由于具有良好的能量吸收能力和广泛的用途，轻质蜂窝金属芯夹层结构（泡沫、蜂窝或格状）已被广泛应用于许多重要领域中的抗爆炸冲击，如车辆、船舶和飞机制造业[1-3]。相对于等效质量的整体固体，夹心板和梁的优点在研究实验[4-7]，数值[8-10]和理论上[11-15]得到广泛的调查。特别是由Fleck和Deshpande [11] 提出的分析模型已成为夹层结构的爆炸/冲击性的理论研究框架。在他们的模型中，夹层结构的整体响应分为三个阶段：流体-结构的相互作用阶段；核心压缩阶段；和整体弯曲和拉伸阶段。基于Fleck和Deshpande [11]的模型，Zhu等人[14]建立了一种预测爆炸载荷下夹芯板永久中心点挠度和响应时间的理论方法。然而，由于大量的弯曲面板已被广泛应用于实践中，爆炸/冲击载荷下夹层壳结构的响应有了研究的必要，从而能够量化保护工程应用中夹层设计的优点。

最近，通过实验研究了泡沫金属夹芯圆柱壳在爆炸/冲击载荷作用下的一些典型的变形失效模式，挠度响应与破坏机理[16-18 ]。弯曲夹层壳的挠度响应与破坏机理变形响应曲面夹层壳与金属泡沫核实验观察，而能量吸收和承载能力则进行了数值研究[19-21]。然而，却少有在可压碎泡沫金属芯的弯夹层壳在冲击荷载作用下的的动力响应的理论预测的研究工作。Li等人[ 22 ]提出了一个非线性可压缩核心模型（包括核心横向柔度）来预测浅层夹层壳的瞬态爆炸响应。在该模型中，在横向方向上的芯的应变通过横向变量的三分之一阶函数来描述，这只对经典的横向刚度模型进行较为深入的预测。后来，Hoo-Fatt和Surabhi [23]开发一个爆炸载荷作用下复合材料夹层圆柱壳预测早期反应，即一种分析模型，通过核心的波过境时间的几个反射。同时，对短夹层管在内爆炸载荷作用下的响应进行了探索性研究，得到了一个显式解析解，并得到了最佳夹层结构[17]。显然，这些现有的理论分析没有涉及到在外部冲击载荷作用下压碎的多孔金属芯夹层圆柱壳的大挠度响应，虽然研究委员会指导类似工程结构的实际设计具有重大的现实意义。

因此，基于Fleck和Deshpande [ 11 ]的三阶段模型的夹层梁和Walters和Jones的整体式课题理论[ 24 ]，本文对圆柱壳提出了一种近似的理论分析以预测用泡沫铝芯的金属夹层壳在爆炸载荷下的冲击响应。这里采用夹层壳的综合屈服轨迹，考虑塑性弯曲和拉伸，并考虑蜂窝芯的强度。

2 实验细节

在本节中简要介绍了鼓风实验过程和结果，并可在[ 25 ]中可以看到详细的描述。

2.1样本

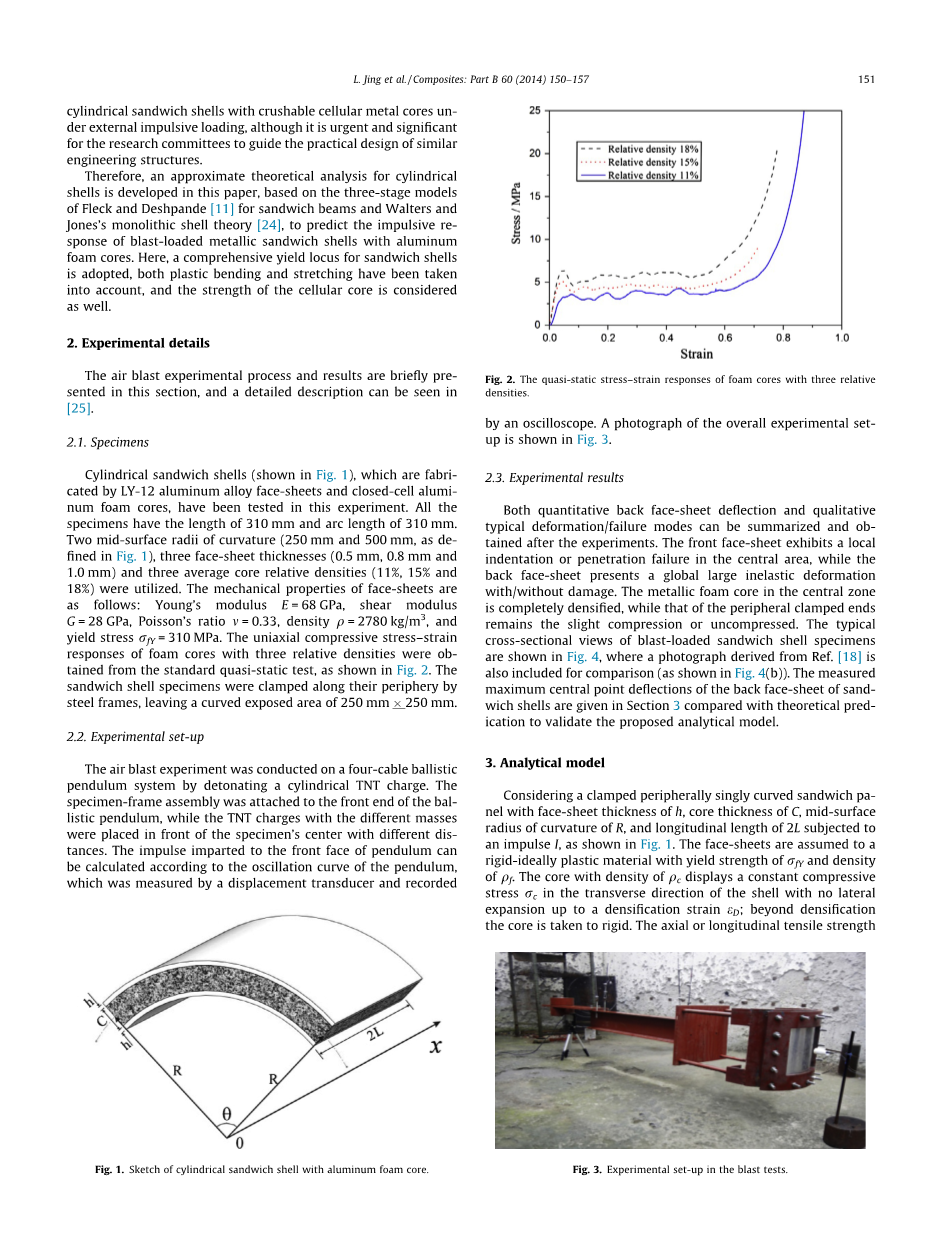
本实验测试由Ly-12铝面板和闭孔泡沫铝芯制造的夹层圆柱壳（见图1）。所有标本的长度为310毫米，弧长为310毫米。实验中使用两个中间表面曲率半径（250毫米和500毫米，如图1所示），三面片材厚度（0.5毫米，0.8毫米和1毫米）和三个平均核心相对密度（11%，15%和18%）。面板材的力学性能如下：杨氏模量E = 68 GPa，剪切模量G = 28 GPa，泊松比为0.33，密度为Q = 2780千克/立方米，和屈服应力为310 MPa。通过标准准静态测试得到由三个相对密度的泡沫芯的单轴压缩应力-应变响应，如图所示2。使用钢框架沿其周边夹紧夹层壳标本，留下一个弯曲的暴露面积为250毫米*250毫米。

图1 泡沫铝夹芯圆柱壳示意图。

图2 三个相对密度泡沫芯的准静态应力-应变响应

2.2实验装置

空中爆炸实验是在一个四电缆弹道摆系统中通过引爆圆柱型TNT炸药来进行。试样架组件连接到的弹道摆的前端，而不同质量的TNT炸药放置在试样的中心前面的不同距离处。根据摆振曲线，利用位移传感器测得的摆振曲线，用示波器记录摆摆给摆前摆面的冲量。图片的整体实验设置如图3所示。

图3 爆破试验中的实验装置

2.3实验结果

实验结束后，可以总结和定量的背面表偏转和定性典型的变形/破坏模式。前面板表现出局部压痕或渗透失败的中心区域，而背面的片材呈现一个覆盖性的非弹性变形大/无损伤。在中心区的金属泡沫芯完全致密化，而周边固支端保持轻微压缩或非压缩。爆炸作用下夹层壳标本的典型横断面视图如图4所示，其中来自参考文献[ 18 ]的照片也用于比较（如图4（b）所示）。在第3节与理论预测验证所提出的分析模型给出了夹心壳的背面片材的最大中心点变形。

图4 测试后夹层壳试样横截面的照片：（a）顶点曲率半径为250 mm，面板厚度1.0 mm，芯厚度10毫米，芯相对密度15%和爆炸冲击17.11 ns；（b）顶点曲率半径为600 mm，面板厚度1.0mm，芯厚度20毫米，芯相对密度9%和爆炸冲击41.2ns[18]。

3 分析模型

考虑一个夹紧外周单弯夹层板，其面板厚度H、芯厚度C、中面曲率半径R和纵向长度2L，受到一个冲击I，如图1所示。假设片材是一个为刚性理想的塑性材料，其屈服强度为,密度为。密度为的核心显示一个恒定的压缩应力在横向方向上壳的横向膨胀没有达到致密化应变；超越致密化的核心采取刚性。轴向或纵向的核心抗拉强度为。与Fleck和其同事[11-13]一样，我们采用三阶段分析框架将夹层圆柱壳体和分裂的夹层壳结构的反应过程分为三个阶段。对于弯曲夹芯板，由于其初始曲率，冲击波可能不均匀地传递到前面片材上。然而，鉴于在爆炸产生的大爆炸前面板，相对较小的尺寸，在正常入射的影响下，假设具有足够的精度，整个面板受到的冲击脉冲是均匀的[26]。类似的假设也在一些现有的对曲面结构研究中采用[22,27,28 ]。因此，假定爆炸脉冲均匀分布在弯曲的夹芯板的前面板上，整个动力响应解耦到相应的三个阶段：

第一阶段：流固耦合阶段，这里忽略根据Fleck和Deshpande [11]验证的讨论，并且整个爆炸冲击I传递到夹层壳结构的前面板。假定前面板立刻获得速度V1，其余的静止。Fleck和Deshpande [11]表示这一阶段的核心压缩程度可以忽略不计。

第二阶段：核心压缩阶段。

第三阶段：整体弯曲和拉伸阶段。

分三个不同的阶段的理由是Fleck和Deshpande [11]观察到三阶段的时间差异显著。图5为一个受冲击载荷作用下夹层壳三级反应示意图。在第一阶段结束后，前面板开始以初始速度V1挤压泡沫芯。然后，在核心压缩阶段用能量效率为基础的方法计算泡沫芯的稳定应力和致密化应变。至于在第三阶段的结构变形，Walters和Jones开发的经典的分析模型 [ 24 ]可圆柱单片壳扩展为夹层壳。

图5 爆炸载荷作用下夹层壳的三阶段反应示意图。

3.1第一阶段：流固耦合阶段

一般情况下，由空气爆炸引起的爆炸过程和冲击波传播是相当复杂的，会有如燃烧反应，导热，空气压缩和爆炸波传播等物理现象。如上所述，认为对夹层壳结构的爆炸冲击在局部区域内均匀分布（也被称为加载区域，在实验数据的基础上验证对曲面夹芯板的研究，在4节中介绍）的前面板。前面板立即获得一个初始速度V1，即，

其中I是前面板受到的爆炸冲击、A0、和h分别是加载区，该面板的质量密度和厚度。

前面板的动能可以通过以下方式计算

3.2 第二阶段：核心压缩

由于在第一阶段爆炸脉冲是均匀分布的，并且实验中[25]核心的压缩主要在中央加载区域可观察到，因此，弯曲夹芯板的压缩阶段可认为类似于平板夹心板。在这个阶段，前面板以V1的初始速度向下移动到压缩泡沫芯。然后，前面板发生大的塑性变形，而背面板由于相对较小的变形量，其状态是固定的，。

在第二阶段结束时，面板和芯获得相等的速度V2，由动量守恒可得：

其中和C分别为泡沫芯的密度和厚度。

相应地，在这个阶段结束时，夹层壳的动能给出如下

所以，在第二阶段的能量吸收可以写为

(5)

或 (6)

其中mu;是核心和面板的质量比并且。

值得注意的是，与核心相比，面板的能量耗散可以忽略不计。因此，能量吸收也可以通过以下方式计算

其中，是泡沫芯的动态平台应力，gamma;是经验常数，和为核心的压缩量。

在这里，我们介绍了Li等人[ 29 ]提出的能量吸收效率应变曲线来计算平台应力和泡沫金属的致密化应变，如图6所示。能量吸收效率定义为在相应的应力值下能量吸收达到给定的正常应变

（8）

其中是屈服点处的应变，相对于开始时的稳定阶段。

在效率应变曲线的固定点处的应变值定义为致密化应变，其中效率值最大，即，

（9）

然后，金属泡沫芯准静态稳定应力写成

使用上述方法，计算三种不同密度的泡沫铝芯的稳定应力和致密应变，实验中在第4节的表1列出。

将式（5）和（6）代入（7），我们可以得到

然后给出泡沫中心的平均压缩应变

应该指出的是，如果按（12）式计算所得的压应变的会大于致密化应变，这表明泡沫芯完全压缩，之后等于。

图6 泡沫铝芯吸能效率-应变和应力-应变关系曲线

3.3第三阶段：整体弯曲和拉伸阶段

考虑弯曲和拉伸的综合效果，Walters和Jones[24]提出圆柱整体壳的解析解，可用于分析受到一定冲击载荷下固体壳结构的有限挠度。在这一部分中，这个模型被修改，并采用一个更全面的屈服准则来预测脉冲加载下金属夹层壳的永久的偏转响应。屈服轨迹，基本构想和解决方案在第3.3.1–3.3.3分别介绍。

表1 理论预测的夹层壳体材料特性

3.3.1夹层壳屈服轨迹

Qiu等[12]修正了由Jones[30]提出的薄而强的薄板和厚而弱的蜂窝芯的夹层结构的屈服准则。

弯矩M0和膜力N0如下

外切正方形轨迹方程为

同样，内接正方形轨迹可以描述为

在本文中，提出来针对夹层圆柱壳一个更全面的夹层结构[ 4,14,31 ]的屈服轨迹，在附录A中有详细描述。在屈服准则中，考虑两者的核心强度和塑性弯曲和强度的影响，假定金属泡沫芯具有相同的拉压力学性能。限定屈服轨迹与式（15）相同，而相应的描绘屈服准则给出

其中

3.3.2基本构想

Walters和Jones [ 24 ]开发了一套近似理论的程序来估计完全夹紧圆柱单片壳冲击下的塑性动力响应。分析中保留有限变形的影响，但材料的弹性，应变硬化和应变速率敏感性被忽略。在目前的研究中，通过前两阶段，在受冲击载荷时金属泡沫夹芯壳已经完全被压成泡沫芯。在第三阶段的力学表现可以采取类似的圆筒形整体壳。因此，在我们的研究中，Walters和Jones [ 24 ]的能量平衡模型可以修改并应用于弯曲夹芯板。控制方程如下

其中m和P3是夹层壳的质量和单位面积压力，并且m = 2h C；W是圆柱壳结构的横向变形；“.”表示对时间的偏导；而“rsquo;”表示对轴向的偏导；，和分别是广义应力；从i到j连续求和。应该指出的是，基于试样的边界能量没有损耗，式（19）可包括的铰链曲线与外壳的物理边界相重合。因此，取消加强限制会导致在外壳边界的外部工作率[ 24 ]。

与经典的单壳理论类似，忽略轴向力的影响，即。在爆炸载去作用下，夹层壳结构获得均匀的速度场。由于其持续时间短，可以忽略不计，在这一阶段方程（19）中P3将消失，即

假设一种运动许可速度场为

其中在跨中（x = L）处的速度。将式（21）代入式（20）得

其中，在x = L处的平面上的对称性要求被用。很明显，周向应变和曲率的圆周变化，这表示

结合式（22）和相应的屈服轨迹，解出近似关联非线性微分方程，可获得夹层圆柱壳的最大中心点挠度。

3.3.3解决方案

在3.3.1中描述了确切的屈服轨迹。在这里，我们首先把外切正方形作为夹层壳的近似屈服轨迹。屈服轨迹的对称性要求如下

将式（24）代入式（22）并求解初始条件下相应的非线性微分方程

当变形结束时速度等于0（即T = t），

在这里，我们引入这些无量纲变量，提出这些方程在无量纲形式

后面板标准的最大中心点偏转和结构响应时间可由下式获得

同样，采用相同的分析但描绘屈服轨迹，我们也有

4 理论预测与实验结

全文共11872字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[144046]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章