多学科设计优化和稳健设计方法在并行工程中的应用
Alessandro Giassi, Sirehna Ramp;D 公司, 南特/法国, alessandro.giassi@irccyn.ec-nantes.fr
Jean-Jacques Maisonneuve, Sirehna Ramp;D 公司, 南特/法国
Fouad Bennis, IRCCYN Laboratory ECN, 南特/法国
摘要
本文用以介绍在并行工程环境下的多学科设计优化方法的实现方式。虽然这些学科在舰船领域的开发依然很薄弱,但是对这一领域的兴趣却在不断增长。此外,本文还介绍了一种基于稳健设计技术的创新的方法MORDACE(并行工程的多学科优化和稳健设计方法)。减摇鳍的优化就是作为介绍这一方法的范例。
1.简介
本文将会介绍一种应用于船舶设计问题的创新的多学科优化方法。它的对象包括更加宽泛的并行工程的结构框架,Winner 等 (1988), 它是现代产品设计过程中的一个基本要素。市场的竞争力以及所需要的特殊的知识和工具推动企业分配能够产生分化的设计工作。参与者的多样性可能会出现在同一家公司中,例如当一个公司由数个部门组成并且企业的工作是在一些网点中组织开展的(联盟企业)。有时,这种多样性又是来自于与其他公司(虚拟企业)或者分包商的合作。
目前远程协作设计过程的关键在于数字模拟及产品数据管理软件(PDM)的使用,Meinecke and Feacute;ru (2002)。这些工具逐步促使产品设计的完全整合。在此背景下,本文提出了一种多学科优化方法,它可以在不需要高层次整合的前提下完成协同设计。减摇鳍的水动力结构优化为我们提供了测试这一新设计方法的机会。为了比较我们的方法,我们也运用两种传统的多学科方法进行了优化过程。
- 研究案例:减摇鳍的优化
本文提出的方法最初是使用一个数学测试函数。这些数学测试使我们能够定义我们的运算方法并且将它与传统的方法进行比较。随后,我们将我们的方法应用在一个多学科优化的实际案例之中去验证我们的结果。
滚转稳定鳍经常安装在船体中部附近舱底弯曲部分的旋转杆上,如图1。鳍的入射角通过一个控制系统不断进行调整,它可以敏锐的感受到船舶的横摇运动。鳍向左发力,它会产生船舶重力中心的横摇力矩以此来对抗波涛汹涌的时刻同时横摇运动将会减少,Lloyd (1989)。 减摇鳍的优化是以一个真实的应用案例为基础的。鳍具有NACA0015对称截面,Crane 等(1989)。图2显示出了主要的维度,即方根和翼尖弦长cr、ct以及跨度b,纵横比a:
a=(2b/c)=(4b/(cr ct))= 2.5 其中c是平均弦 (1)
优化过程是多科处理的:为了提高水动力结构的性能,我们不断修改着减摇鳍的外部形状和内部架构,以提高这流体动力性能和结构性能。因此,用三目标函数来得出流体力学限制和两个目标函数来得出的结构优化限制。此外,遵守其他一些流体动力学和结构优化的限制。
1950 mm
as 0 寸(N(N
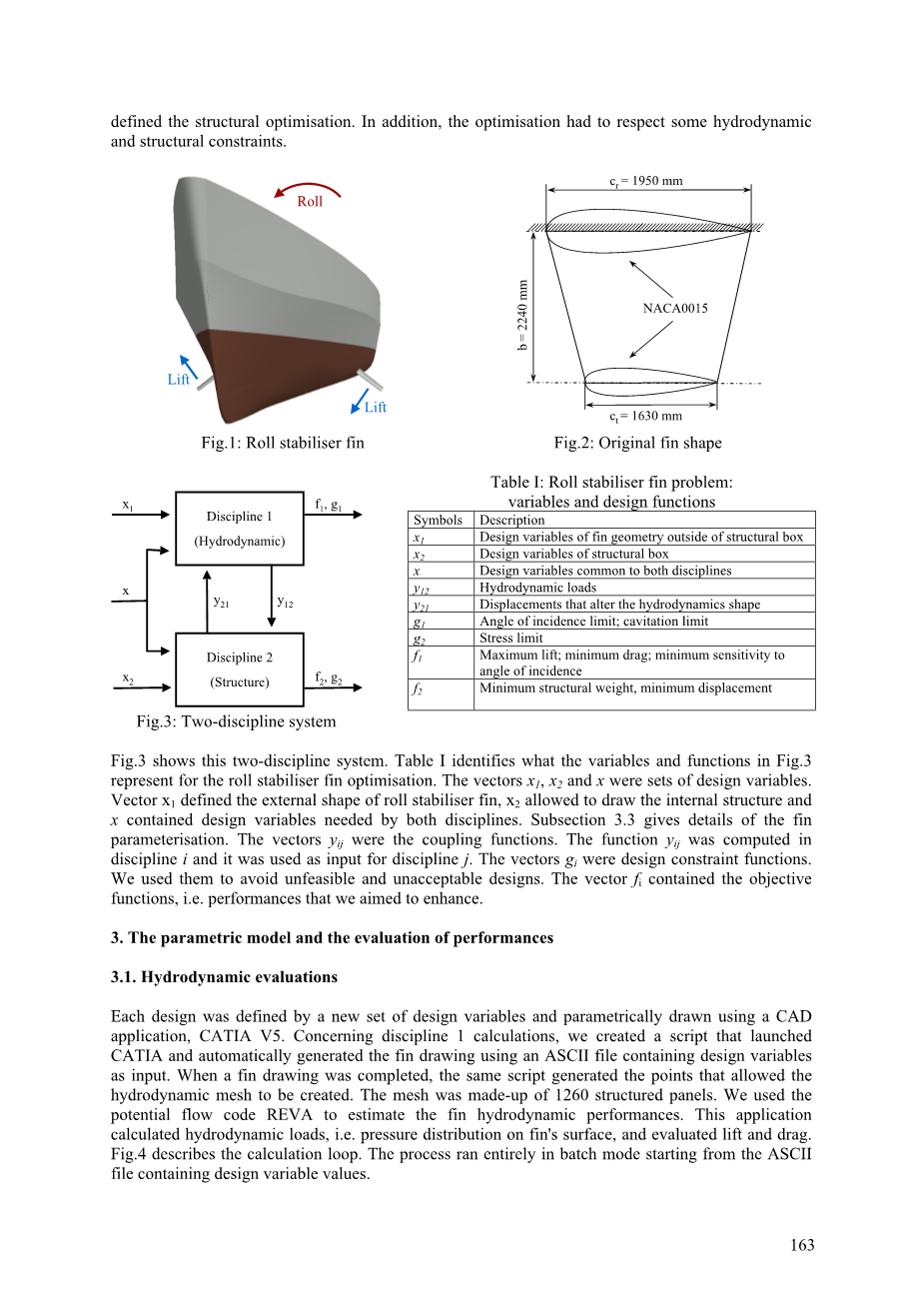
图1:减摇稳定鳍 图2: 原鳍形状
表I: 减摇稳定鳍问题:变量和设计函数
|
符号 |
描述 |
|
x1 |
结构框架外的鳍几何设计变量 box |
|
x2 |
结构框架设计变量 |
|
x |
两个学科的共同设计变量 |
|
y12 |
水动力负荷 |
|
y21 |
改变水动力学形状的位移 |
|
g1 |
攻角极限;涡空极限 |
|
g2 |
应力极限 |
|
f1 |
最大升力;最小阻力;最小攻角灵敏度 |
|
f2 |
最小结构重量,最小位移 |
图3:双学科体系
图3显示该双学科体系。表I指出图3哪些变量和函数代表减摇稳定鳍的优化。向量xh X2 和x为设计变量集。向量xi定义减摇稳定鳍的外形,X2绘制内部结构,而x包含两门学科所需设计变量。第3.3节给出鳍的参数化细节。向量y是组合函数。y函数在学科i中计算,作为学科j的输入值。向量g是设计的约束函数。我们利用它来避免无法实现、不符合要求的设计。向量fx包含目标函数,即我们所要增强的性能。
-
- 参数化模型和性能评估
- 水动力评估
每个设计都用一组新设计变量集进行定义,利用CAD程序和CATIA V5进行参数化绘制。对于学科 1的计算,我们创建脚本,启动CATIA,利用包含设计变量输入值的ASCII文件自动生成鳍图。鳍图绘制完毕后,相同脚本生成点,以建立水动力网格。该网格由1260个结构面板组成。我们利用势流代码REV A,估算鳍的水动力性能。该应用程序计算水动力负荷,即鳍面的压力分布,计算升力和阻力。图4显示计算循环。这一过程由包含设计变量值的ASCII文件开始,完全按照批处理模式运行。
图4:水动力计算循环
水动力优化过程旨在使阻力最小化,升力最大化。第三个目标函数是尽量降低攻角变化的影响。事实上,我们将船舶纵摇运动视为可改变减摇稳定鳍攻角的外部噪音。控制系统将纵摇运动纳入考虑,并修正攻角。因此,我们试图找到一种稳健的设计方案,以尽量降低控制系统的干预。REVA计算不同攻角alpha;i设计方案的水动力性能。因此,水动力优化的三个目标函数正式定义如下:
最大化:
最小化:
最小化:
方程(2)-(4)表明,前两个目标函数是性能值的均值,而第三个目标函数是正规化标准差之和。方程(5)表明,我们将性能值标准差除以原设计的性能值,使其正规化。这样,我们便可以求出方程(4) 一致值(coherent value)之和。(注:我们没有使用相对标准差,因为它会影响低阻力设计)水动力优化必须符合涡空极限和攻角的约束函数。对于涡空约束,鳍面最小容许压力设定为17000 Pa。而对于攻角极限,我们评估Whicker和Fehlner (1958)的方程:
a遵循方程(1)。设计遵守该约束,因为所施加攻角变化的上限alpha;stall gt; 7.5°。
我们利用CAD程序CATIA V5绘制鳍结构。与之前一样,我们采用CATIA脚本技术。我们创建脚本,启动CATIA,利用包含设计变量输入值的ASCII文件自动生成鳍图。在鳍图绘制完毕后,相同脚本启动有限元计算,估算结构性能值。有限元代码采用创成式零件结构分析,一种内部CATIA V5工具。该应用程序自动生成由29592个线性四面体组成的非结构化网格。因此,计算过程由包含设计变量值的ASCII文件开始,完全由CATIA按照批处理模式进行,如图5所示。
图5:结构计算循环
优化过程旨在使结构重量最小化,结构刚度最大化,即最大节点位移最小化。我们施与应力约束。所选择的钢材最大接受应力为200MPa。我们将结构优化问题规范化为:
发现 设计变量 x,x2 = (x1, ... ,xn)
满足 约束 g21(x, x2) = 最大应力= (x, x2)lt; 200 MPa
最小化 目标函数 f21(x, x2) =结构重量
f22(x, x2)= 最大节点位移
对于组合函数,我们只考虑y12,即用流场解算器来计算水动力负荷。我们认为y21太小,不足以改变水动力形状。事实上,原鳍形状的最大位移为13.5毫米 (鳍跨度的0.5%)。我们试图将其最小化。因此,性能值无迭代计算。
3.3. 参数化
在开始优化过程前,我们必须对问题进行几何定义。优化算法必须能够寻找设计变量变化与性能值进化之间的关系。因此,我们必须对原鳍设计进行可控修改。在分析减摇稳定鳍的不同行为时,该优化过程涉及两个学科,需要两种不同参数化模型。水动力学科旨在简化表面,而结构学科旨在对定义内部几何结构的参数(如厚度值、加强件分布和截面积等)进行修改。
参数的选择至关重要,因为它定义了优化问题的数学模型。生成解很大程度上取决于所选参数,因为它们定义了研究的空间。参数化步骤的另一个重要层面是参数边界值的定义。为了扩展原始鳍设计周围的设计空间,覆盖可行域,参数应当有较宽的边界值。然而不幸的是,宽边界值的参数化可能产生许多无法实现的配置,即无法利用应用程序计算性能的鳍设计。流场和结构计算需要改编网格的鳍设计参数进化函数,因此如果参数变化较大,可能造成网格扭曲。网格的生成应当尽量稳健,否则,参数化应当通过原稳定鳍初始值周围的短暂变化进行。本研究的水动力表面网格很容易生成,因此,边界值很大(初始值周围20%)。鳍几何结构的复杂性需要我们小心作出选择。图6显示鳍面参数和内部结构参数。表II描述参数及其初始值。
图6:a)水动力参数;b)结构参数
表II:参数表
|
参数 |
描述 |
初始值 |
|
LOut |
延伸长度 |
2240 mm |
|
Li |
截面i的花键长 |
1950 / 1630 mm |
|
Thici |
截面I的半值厚度 |
0.15 Li/2 |
|
LThici |
最大厚度点位置 |
0.25 Li |
|
Nozi |
主轴前缘位置 |
0.3 Li |
|
ti1 |
前缘截面i花键的张力 |
0.95 |
|
ti2 |
后缘截面i花键的张力 |
0.55 |
|
ti3 |
最大厚度点截面i花键的张力 |
1.30 |
|
R1 |
齿根半径 |
90 mm |
|
R2 |
齿顶半径 |
50 mm |
|
Di 全文共11325字,剩余内容已隐藏,支付完成后下载完整资料
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料 资料编号:[154750],资料为PDF文档或Word文档,PDF文档可免费转换为Word |
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。
您可能感兴趣的文章
- 船舶在浅水航道中航行时的岸壁效应数值研究外文翻译资料
- 基于三维面元法限制水域船体下蹲的数值研究外文翻译资料
- 关于甲板大开口船体梁极限抗扭强度的实验研究外文翻译资料
- 基于斯托克斯方程计算和系统识别 方法预估实船操纵模型参数外文翻译资料
- 水面舰艇5415在PMM演习中的基准CFD验 证数据-第二部分:平均相位的立体PIV流 场测量外文翻译资料
- 初步设计阶段船舶功率推进预测第二部分初步设计中有用的服务速度船舶功率推进数学模型外文翻译资料
- 对某高速船模湍流自由表面的数值与试验研究外文翻译资料
- 第三章水下搜救与恢复操作外文翻译资料
- 液化天然气供求关系的现状与展望:一个全球性展望外文翻译资料
- 基于CFD的高层钢结构建筑风效应数值评估外文翻译资料