
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
Chameleon:基于动态建模的层次聚类
许多高级算法很难处理高度可变的且不遵循预设模型的数据簇。基于互联性和紧密性,Chameleon算法为这些高度可变的聚类提供了精确的结果。
聚类是数据挖掘中的一个发现的过程。它以最大化提高簇内的相似性和最小化两个不同簇间的相似性的方式对一组数据进行分组。 这些已挖掘的簇可以帮助解释潜在数据分布的特点,并用以其他数据挖掘和分析技术的基础。聚类对于基于购买模式的客户群分组、Web文档分类、具有类似功能的基因和蛋白质分组、根据地震数据对易发生地震的空间位置进行分组等很有效。
大多数现有的聚类算法都会找到适合某些静态模型的聚类。虽然在某些情况下有效,但这些算法可能会崩溃——如果用户没有选择合适的参数,这会错误地聚类。而且有时模型无法充分捕捉簇的特征。 当数据包含不同形状,密度和大小的簇时,大多数算法都会崩溃。
现有算法使用簇的静态模型,但在合并时没有利用有关各个群集的性质信息。此外,一系列的方案(CURE算法和相关方案)忽略了关于两个集群中所有数据点的聚合互连性的信息。另一组方案(ROCK算法,组平均方法和相关方案)忽略关于两个簇的接近度的信息,接近度定义为两个簇中最接近的数据点的相似性。(有关更多信息,请参阅“传统聚类算法”侧栏。)
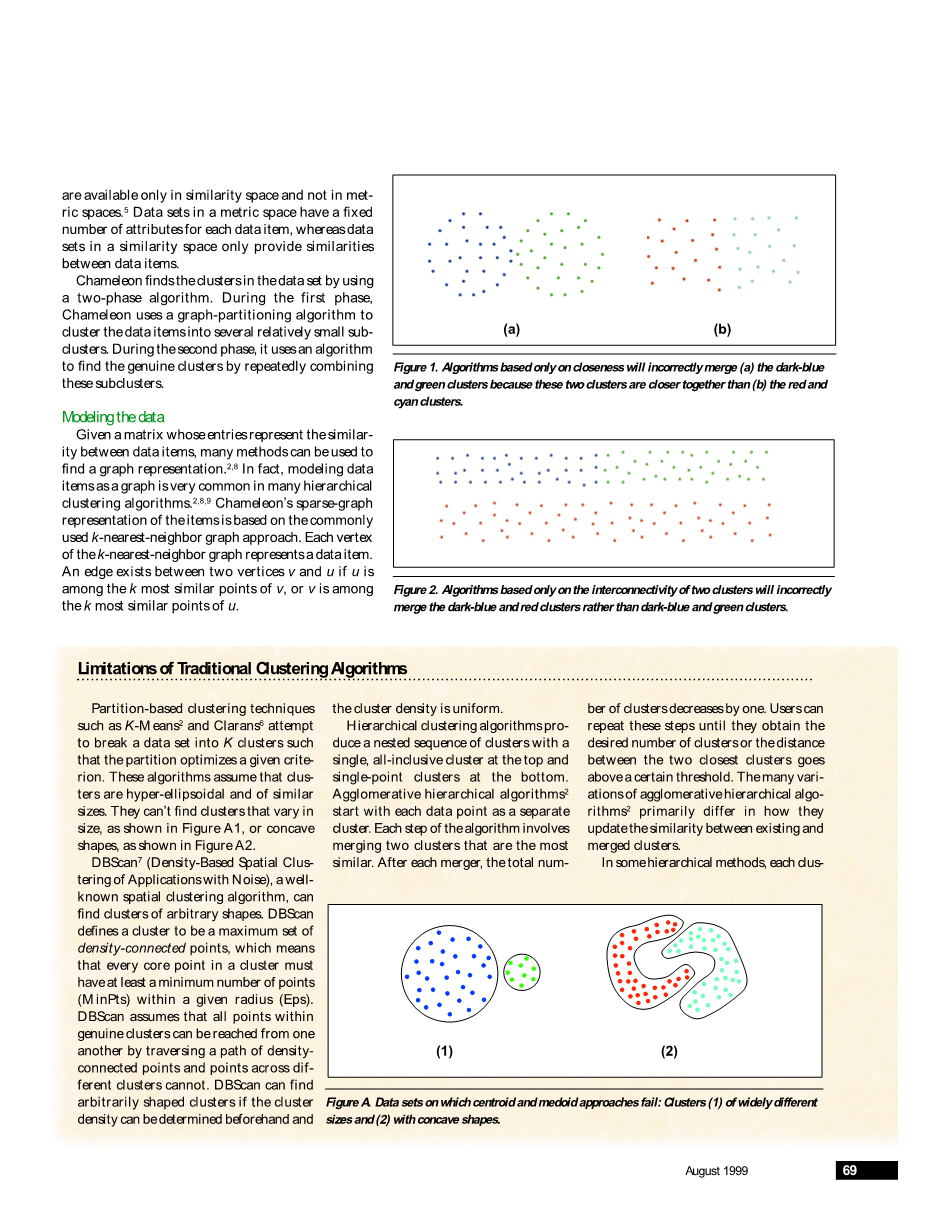
通过仅考虑互连性和密切性的两者之一,这些算法就会容易错误地地选择和合并一对簇。 例如,一种仅关注两个簇的紧密度的算法将错误地合并图1a中的簇而不是图1b的簇。类似地,在图2中,仅关注互连性的算法错误地将深蓝色与红色簇而不是绿色簇合并。这里,我们是假设深蓝色和红色簇中的数据点之间的聚合互连性大于深蓝色和绿色聚类的聚合。然而,深蓝色簇的边界点比绿色簇的边界点更接近于红色簇的边界点。
传统聚类算法的局限性
基于分区的聚类技术(如K-Means和Clarans)尝试将数据集分解为K个集群,以便分区优化给定的标准。 这些算法假设簇是超椭圆体的并且具有相似的尺寸。 他们可以找到大小不同的簇,如图A1所示,或凹形,如图A2所示。
DBScan(基于密度空间的噪声应用聚类)是一种著名的可以找到任意形状簇的空间聚类算法。 DBScan将簇定义为密度连接点的最大集合,这意味着簇中的每个核心点必须至少具有给定半径(Eps)内的最小数据点个数(MinPts)。
DBScan假设真正簇中的所有点都可以通过遍历密度连接点的路径彼此到达,而跨越不同簇的数据点不能。如果可以预先确定簇密度且密度统一,则DBScan可以找到任意形状的簇。
层次聚类算法产生嵌套的聚类序列,其顶部是整个簇,底部是单点簇。凝聚型层次算法以每个数据点作为单独的聚类开始。 算法的每个步骤都涉及合并两个最相似的聚类。 每次合并后,集群总数减少一个。 用户可以重复这些步骤,直到他们获得所需数量的簇或两个最接近的聚类之间的距离超过某个阈值。凝聚型层次算法的许多不同主要在于它们如何确定(更新)已有簇和被合并簇之间的相似性。
在一些层次方法中,每个簇由质心或中心(最接近聚类中心的数据点)表示,两个簇之间的相似性通过质心/中心体之间的相似性来测量。 对于簇中的数据点更靠近另一簇的中心而不是其自身簇的中心的数据,这两种方案均失败。这种情况发生在许多自然簇中,例如,如果簇大小存在很大差异,如图A1所示,或者当簇形状为凹形时,如图A2所示。
单链接层次方法通过属于不同簇的最近数据点对的相似性来测量两个簇之间的相似性。与基于质心/基于类中心的方法不同,此方法可以找到任意形状和不同大小的簇。 但是,它非常容易受到噪声数据,异常值和伪数据的影响。
研究人员提出了CURE(使用代表点聚类)来弥补这两种方法的缺点,同时结合它们的优点。 在CURE中,根据收缩因子选择固定数量的散射点并将它们缩小到簇的质心来表示簇。CURE通过属于不同点的最近的一对数据点的相似度来测量两个簇之间的相似性。
与基于质心/基于类中心的方法不同,CURE可以找到任意形状和大小的簇,因为它通过多个代表点表示每个簇。 将代表点缩小到质心让CURE避免与噪声和异常值相关的一些问题。 但是,这些技术无法解释各个簇的特殊特征。当原始数据不遵循假设模型或存在噪声时,它们可能会做出错误的合并决策。
在一些算法中,两个聚类之间的相似性通过属于不同聚类的数据对之间的相似性(即互连性)的合并来捕获。这种方法的基本原理是属于同一群集的子群将倾向于具有高互连性。但两个集群之间的总互连性取决于集群的规模;通常,成对的较大簇具有更高的互连性。
许多这样的方案相对于所涉及的簇的预期互连性去规范化一对簇之间的合并相似性。例如,广泛使用的组平均方法假设完全连接的簇并在两个簇之间通过ntimes;m缩放合并的相似性,其中n和m是两个簇中的数据点数目。
Rock(使用链接的鲁棒聚类)是一种最近开发的算法,它在派生的相似性图上运行,根据用户指定的互连模型去缩放凝聚的互连性。但是,所有这些方案的主要限制是它们假定了一个用户提供的静态的互连模型。这样的模型不灵活,当模型低估或高估数据集的互连性或当不同的簇表现出不同的互连特征时,很容易导致错误的合并决策。虽然有些方案允许不同问题领域的连接性不同(Rock也是如此),但无论密度和形状如何,所有簇的连接仍然都是相同的。
图A.质心和近形方法失败的数据集:(1)大小不同的簇;(2)凹形。
Chameleon:基于动态建模的层次聚类
Chameleon是一种新的克服了现有聚类算法的局限性的凝聚型层次聚类算法。图3概述了用Chameleon在数据集中查找簇的总体方法。
Chameleon算法的主要特点是,它在识别最相似的一对簇时,既考虑了互连性,又考虑了亲密性。因此,它避免了前面讨论的算法的限制。此外,Chameleon使用了一种新的方法来衡量每一对簇之间的互联性和紧密性。这种方法考虑到群自身的内部特性。因此,它不依赖于静态的、用户提供的模型,并且能够自动适应合并后的簇的内部特性。
Chameleon在稀疏图上操作,其中节点表示数据点,加权边表示数据点之间的相似性。这种稀疏图表示,允许Chameleon缩放到大数据集和成功使用仅在相似度空间而不是测度空间的数据集。在测度空间下的数据集每个数据点有固定数目的属性,而在相似度空间下的数据集只需提供数据点之间的相似度。
Chameleon通过两个阶段的算法在数据集中找到簇。在第一阶段,Chameleon使用一个图分区算法将数据点聚类为几个相对小的子簇。在第二阶段,它使用一种算法通过重复合并找到真正的簇。
数据建模
给定一个条目表示数据点之间相似性的矩阵,许多方法可以用来找到一个图的表示。事实上,将数据点建模为一个图在许多层次聚类算法中是很常见的。Chameleon的数据点的稀疏图表示是基于常用的k-最近邻图方法。k-最近邻图的每个顶点表示数据点。如果u在v的k个最相似点,或者v在u的k个最近相似点中,则在两个顶点v和u之间存在一条边。
图1.仅基于贴近度的算法将错误地合并(a)深蓝色和绿色的聚类,因为这两个聚类比(b)红色和青色的聚类更接近。
图2.仅基于两个簇的互联性的算法将错误地合并深蓝色和红色簇,而不是深蓝色和绿色簇。
图4显示了简单数据集的1,2和3最近邻图。使用k最近邻图表示要聚类的项目有几个优点。相距很远的数据项与权重完全断开在边缘捕获空间的潜在人口密度。更密集和更稀疏区域中的项目被统一建模,并且表示的稀疏性导致计算上有效的算法。因为Chameleon在稀疏图上运行,所以每个集群只不过是数据集的原始稀疏图表示的子图。
图3.Chameleon使用两阶段算法,首先将数据项划分为子集群,然后反复组合这些子集群以获得最终的集群。
簇的相似度建模
Chameleon通过查看它们的相对互连性(RI)和相对接近度(RC)使用动态建模框架来确定簇对之间的相似性。Chameleon选择要合并的是RI和RC数值都为高的一对簇。也就是说,它选择互连良好且紧密相连的簇。
相对互联性。聚类算法通常根据边缘切割来测量簇和之间的绝对互连,边缘切割是横跨两个聚类的边缘的权重之和,我们表示为。簇之间的相对互连是它们相对于其内部互连性标准化的绝对互连。为了获得簇的内部互连性,我们通过将簇分成几乎相对两部分的最小二分切割的边进行求和。最近图划分的进步使得有效地找到这样的量成为可能。
因此,簇和之间的相对互连性表示为:
。
通过关注相关互连性,Chameleon能够克服现有算法存在的使用固定互连模型的局限性。相对互连性能对簇形状的不同之处和不同簇的互连的程度不同做出解释。
相对亲密性。相对亲密性(也译作相对亲密度)涉及的概念类似于为相对互联而开发的概念。簇的绝对贴近度是平均重量(相对于权重f之和)。 将CI中的顶点与CJ中的顶点连接起来的边。由于这些连接来自k-最近邻图,它们的平均强度为af提供了一个很好的度量。 沿着两个群集的接口层的数据项之间的finity。同时,该措施可接受离群值和噪声值。
图4.二维原始数据中的K-最近邻图:(A)原始数据,(B)1-,(C)2-和(D)3-最近邻图
为了得到一个簇的内部亲密度,我们需要通过最小二分切割(将簇分割成两个大致相等的部分)的边的权重的平均值。
一对簇之间的两个簇的内部亲密性是归一化两个簇的内部亲密的相对亲密度:
其中是连接和两个簇的边的平均权值,和分别是属于簇的最小平分切割的边的平均权重,术语和是每个簇中的数据点个数。这个方程式通过按内部加权平均值计算和内部亲密度而规范化两个簇的绝对亲密度。 这阻止了小的稀疏簇合并成为大的密集簇。
一般情况下,两个簇之间的相对贴近度小于一个,因为在不同簇中连接顶点的边具有较小的权重。通过关注相对紧密性,Chameleon可以克服现有算法的局限性,这些算法只关注绝对的接近性。通过观察相对的紧密性,Chameleon正确地融合了簇,从而产生簇的项目之间有一个一致的紧密程度。
过程
用于建模簇的相似度的动态框架仅在每个集群包含足够大量的顶点(数据项)时才适用。原因在于,为了计算集群的相对互连性和紧密性,Chameleon需要计算每个集群的内部互连性和紧密性,这两者都无法准确计算包含少量数据点的集群。因此,Chameleon有一个第一阶段,它将数据点聚类成几个包含足够数量项的子簇去动态建模。在第二阶段,它通过使用动态建模框架分层合并这些子簇来发现数据集中的真正簇。
Chameleon使用hMetis找到了最初的子簇,这是一个快速、高质量的图分区算法。 hMetis将数据集的k-最近邻图分割成几个分区,以便最小化边缘切割。由于k近邻图中的每个边表示数据点之间的相似性,因此最小化边切割的分区有效地最小化了跨分区的数据点之间的关系(亲和性)。
在找到子簇后,Chameleon使用相对互连性和相对亲密度切换到重复组合这些小的子簇的算法。有许多方法可以开发一种算法来解释这两种方法。Chameleon使用两种不同的方案。
自定义阈值。第一个仅合并那些超过用户指定的相对互连(TRI)和相对接近度(TRC)阈值的簇。在这种方法中,Chameleon访问每个簇Ci并检查相邻的簇Cj,RI和RC超过这些阈值。
如果不止一个相邻的簇满足这些条件,那么Chameleon将Ci与它最连接的簇合并 - 即,具有最高绝对互连性的对Ci和Cj。
一旦Chameleon为每个集群选择了一个合作伙伴,它就会执行这些合并并重复整个过程。用户可以使用TRI和TRC控制所需群集的特征。
函数定义的优化。在Chameleon中实现的第二种方案使用一个函数将相对连通性和相对贴近度结合起来。Chameleon选择最大的簇对 改变这个功能。由于我们的目标是合并相对连通性和相对紧密性都很高的对,因此定义这种函数的一种自然方法是获取它们的乘积。选择最大的簇。这个公式对这两个参数都具有同等的重要性。然而,通常我们可能会更倾向于给予更高偏好的集群。 这两项措施中。由于这个原因,Chameleon选择了一对最大的集群:
其中alpha;是用户指定的参数。当alpha;gt;1时,Chameleon对相对贴近度的重视程度较高,当alpha;lt;1时,相对连通性较高。
图5.我们实验中使用的四个数据集:(a)DS1有8000点;(b)DS2有6000点;(c)DS3有10000点;(d)DS4有8000点。
图6.由Chameleon发现的四个数据集的聚类簇。
图7.用收缩因子0.3,代表点数等10的CURE识别的簇。对于DS3,CURE首先合并属于两个不同子集群的子簇(a)25个簇。使用(b)指定的11个簇-与Chameleon发现的相同的数目——CURE显示的结果。CURE为DS4指定了(c)25和(d)8
提供了这些结果。
结果和比较
我们在四个不同的数据集上比较了Chameleon与CURE和DBScan的性能。这些数据集包含6000到10000个二维点,这些点的几何形状如图5所示。这些数据集表示了一些聚类困难实例,因为它们包含任意形状、邻近性、方向和变化密度的簇。它们也有很大的噪音和特殊的人造数据。这些结果很多都可以在http://www.cs.
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[20823],资料为PDF文档或Word文档,PDF文档可免费转换为Word


