Booth 乘法器：方便乘法外文翻译资料

 2022-10-22 16:50:03

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

Booth 乘法器：方便乘法

Deepali Chandel1, Gagan Kumawat2, Pranay Lahoty3, Vidhi Vart Chandrodaya4, Shailendra Sharma5

1,2B.Tech. Student, 3Assistant Professor, Arya Institute of Engineering amp; Technology, Jaipur (Raj.), India4,5M.Tech. Student, Jagannath University, Jaipur (Raj.), India

摘要

在硬件中的乘法可以用2种方式来实现，无论是通过使用更多的硬件实现快速执行或通过使用更少的硬件实现的缓慢执行。乘法器的面积和速度是一个重要的问题，大面积的消耗会使速度增加，反之亦然。乘法器在大多数高性能系统中起着至关重要的作用。一个系统的性能在很大程度上取决于乘法器的性能，因此乘法器应该是快速的，并且消耗更少的区域和硬件。这种想法迫使我们研究和审查有关Booth算法，改进Booth算法和其基-2、基-4，基-8形式。

关键词：Booth算法；改进的Booth算法；乘法；乘法器；基-2；基-4；基-8。

Ⅰ 引言

Booth算法应用于有符号数字的相乘是一个明智之举。它启用加法和减法的能力，用多种方法来计算一个产品[5]。Booth算法是一种利用二进制符号的二进制数的乘法算法[9]。

早期的乘法是一般通过序列的加减法运算，然后再移位操作。乘法可以很好的看作一系列重复的加法。会增加的数作为被乘数，和它被增加的次数作为乘法器，我们得到的结果是乘法结果。在此后每一步，产生部分产品。当操作数是整数时，产品一般是两倍的操作数的长度，以保护信息内容。这种重复的加法方法是算术定义推荐的慢方法，因为它总是被一种利用位置描述的算法所代替。

我们可以把乘法器分解成两部分。第一部分是对部分结果的生成，其次是对部分结果的收集，然后进行补充。基本乘法原理是双重的，即部分结果的评价和转移部分结果的收集。这是由转移部分乘积矩阵列的连续增加执行。

“乘法器”的有效转移，得到适当位数的“被乘数”。延迟门控的情况下被乘数都必须在同一列中转移部分积矩阵。然后，它们以特殊形式被添加到形成的结果的位数中。乘法就是这样一个多操作数操作。要将乘法扩展到有符号数和无符号数，一个合适的数字系统将是以双补充格式的数字描述。

Ⅱ 背景

这个算法是1950年Andrew Donald Booth在伦敦布卢姆斯伯里的伯克贝克学院做研究时发明的。Booth使用的接待台式计算器增加并形成了提高速度的算法，转移速度变快。Booth算法在计算机体系结构的研究中是很重要的[14]。

Andrew Donald Booth是伯克贝克学院计算机先驱小组的负责人。Andrew Donald Booth出生于1918年2月11日，死于2009年11月29日。Booth在人力和财力上资源不足，并强调建设规模较小的机器[15]。Andrew Donald Booth是领导创新以计算机为主导的磁鼓存储器和发明了Booth乘法算法的英国电气工程师，计算机科学家和物理学家。Booth成长于Weybridge和Surrey，就读于Haberdashers Askes 男子学校。

Ⅲ 乘法算法

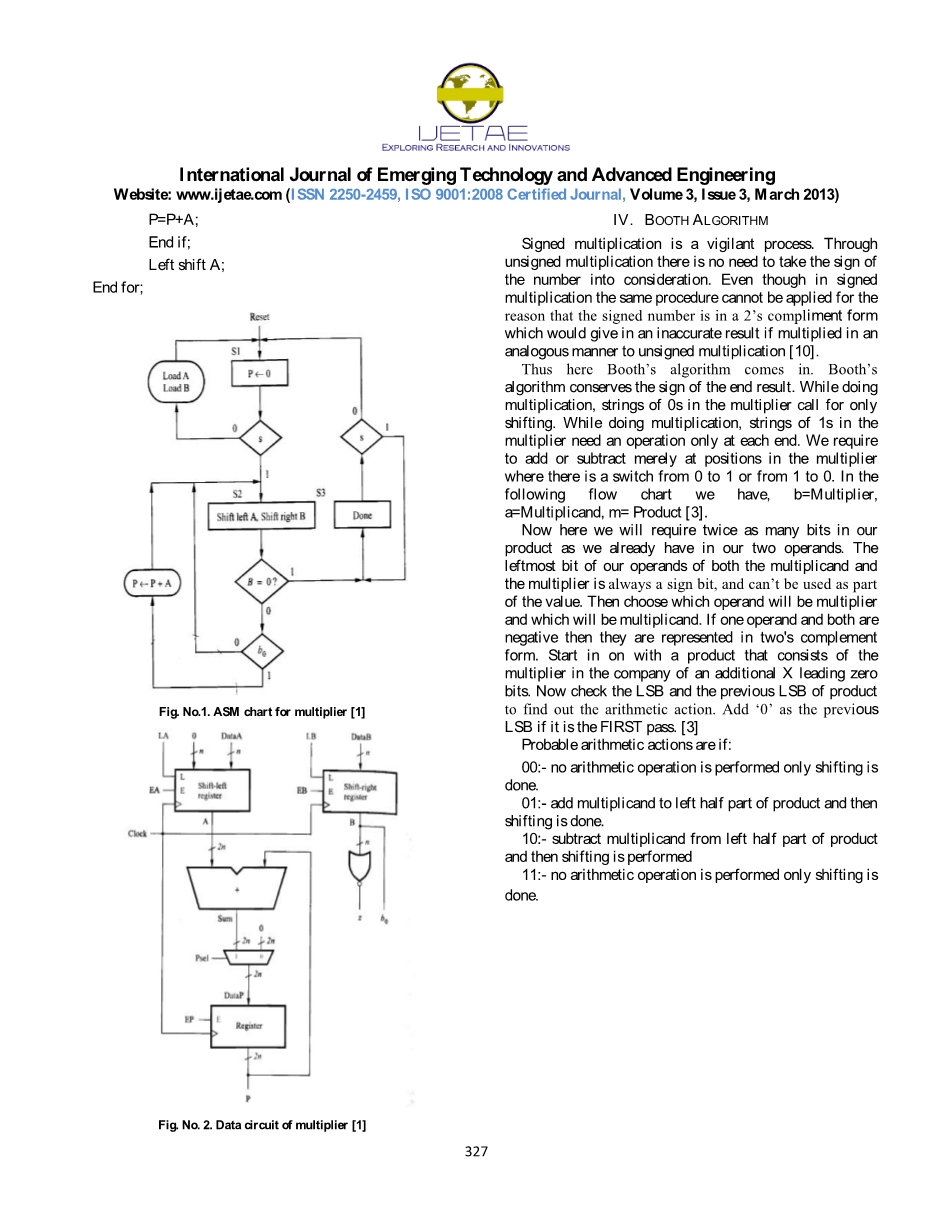
一个乘以两符号的n位二进制数，且采用二维阵列相同的子电路的电路。每一个包含了一个全加器和一个“和”电波传送。对于大量的位数，这样的做法可能不恰当，因为需要大量的电波传送。另一种是使用移位寄存器与加法器相结合来实现传统的乘法运算的方法[1]。

P=0；

For i=0 to n-1 do

If bi=1 then

P=P A；

End if；

Left shift A；

End for；

图1 乘法器ASM图表[1]

图2 乘法器的数据电路[1]

Ⅳ Booth算法

符号乘法是一个警惕的过程。通过无符号乘法，没有必要把这个数字的符号考虑进去。即使在符号乘法相同的过程不能被应用，原因是符号数字在一个二补码形式如果乘一个类似于无符号乘法的方法，会给出一个不准确的结果[10]。

因此，引入Booth算法。Booth算法是保存最终结果的标志。而做乘法，只有转移乘数时调用0字符串。而做乘法，在乘1字符串只需要操作每一端。我们需要在乘法器中增加或减去的位置，其中有一个转换从0到1或从1到0的位置。在下面的流程图中，b=乘法器，a=被乘数，m=结果[3]。

现在这里，我们将需要两倍作为我们的结果中的许多位数，因为我们已经储存了我们的双操作数。最左边的位操作数的被乘数和乘数始终是符号位，不能作为价值的一部分。然后选择操作数作为乘数和被乘数。如果一个操作数两个都是负的，那么它们被表示为二补码形式。开始在一个结果，由乘数和一个额外的times;领先的零位的公司乘数组成。现在检查LSB和以前的LSB结果找出算术行动。如果它是第一个通过，添加“0”作为以前的LSB。

可能的算术动作：

00:- 没有进行算术运算，只进行移位。

01:- 加被乘数左半部分结果，然后移位。

10:- 减被乘数左半部分结果，然后移位。

11:- 没有进行算术运算，只进行移位。

图3 Booth乘法运算[3]

例如：

10乘以7用5位数字（10位结果）。

10的二进制是01010

-10的二进制是10110（因此现在我们需要减去被乘数时可以添加10110）

-7的二进制是11001

我们的预期结果应该是（70）的二进制（1110111010）。

算法步骤：

步骤1：（00000 11001 0）现在最后两位是10，因此这里00000 10110 =10110。现在我们得到（11001 11001 0），现在通过ARS（算术右移）得到（11011 011001）。

步骤2：最后两位是01，因此11011 01010=00101（进位被忽略，因为此外 ve和-ve不能溢出。现在我们得到（00101 01100 1）现在通过ARS我们得到（00010 0 1011 0）。

步骤3：最后两位是00，只有ARS改变才能完成，现在我们将会得到（00001 01011 0）。

步骤4：最后两位是10，因此00001 10110=10111，现在我们将得到（10111 01011 0），通过ARS我们将会得到（11011 10101 1）

步骤5：最后两位是11，只有ARS才能发生改变，现在我将得到（11101 11010 1）。

步骤6：现在忽略最后一位，我们将得到结果（11101 11010）= -70[9]。

Ⅴ 改进Booth算法

改进的Booth算法是Booth算法的速度的两倍。改进的Booth编码算法是一种有效减少部分结果的数量，通过分组两个操作数中的一个连续位，形成符号倍数。Booth编码的操作数被称为乘法器，其他操作数被称为被乘数。

A. 基-2

Booth算法为符号二补码形式的二进制整数提供了一个乘法过程。

例如：2在十进制times;（-4）中，即二进制0010times;1100。

步骤1：Booth表[12]

1. 在这两者中，选择一个连续序列中的最小差异的数字，把它看作为乘数。

即0010—0到0没有变化，0到1是一种变化，1到0是另一种变化，因此这里存在两种变化，0到0没有变化，1100—1到1没有变化，1到0是一种变化，0到0没有变化，因此这里仅有一种变化。因此，乘法2*（-4），其中（0010）是作为被乘数，（1100）作为乘数。

2. 现在X=1100是乘数，Y=0010是被乘数。现在把Y采取二补码形式，并看作-Y，即-Y=1110.

3. 把X值代入表中

4. 把0代入X-1等同于前面一个X的LSB值。

5. 把0代入U和V行，操作后得到包含X和Y的结果。

6. 每4行作为一个周期，我们必须乘以4位数字。

步骤2：Booth算法需要评估乘数的位数和部分结果的转移。转移之前，被乘数可能被添加到之前的部分结果中。

可能是减去部分结果，或可能是左侧不变，根据以下规则：

观察乘数X的第一位LBS值，和乘数X-1的之前最少但最重要的位数。

现在观察位数。

00：转移

11：转移

01：把Y代入U，然后转移

10：从U减去Y，然后转移，或者把-Y代入U执行，然后转移。

Ⅱ. 把U amp; V一起考虑，通过算术右移位（ARS），节省了二补码形式的符号位。

通过正数剩下的正，负数剩下的负。

Ⅲ. 现在用循环右转移X，这将阻止我们使用X的2个寄存器的值。

B. 基-4

基-4 Booth算法扫描字符串的3位给出下面的算法：

1. 如果需要的话，可延伸了标志位1的位置，保证只有n。

2. 在最小的乘法器的右边附加一个0。

3. 根据每一个矢量的部分值。

结果可能为0， Y，-Y， 2Y，-2Y。Y的负值被认为是以二补码形式的Booth重新编码乘数术语，我们必须考虑三位为一组，在一个方法中，每个组与前一个组的位重叠。从LSB开始分组，第一组只使用2位得乘法器[12]。

让我们举个例子：

被乘数是（001011）

乘数是（010011）

现我们把三位为一组考虑为乘数[11][13]。

基-4 Booth算法器的编码将根据以下表格做：

表格Ⅱ

基-4 Booth乘法器编码[16][4][6][7]

groups

Partial products

000

0

001

1*multiplicand

010

1*multiplicand

011

2*multiplicand

100

-2*multiplicand

101

-1*multiplicand

110

-1*multiplicand

111

0

根据表格2我们知道：

（010）—1

（001）—1

（110）—（-1）

因此被乘数与三编码的位数是1,1和-1。

（i）-1*（001011）

=001011

现在1111被代入结果中，因为负值符号。因此-1乘法运算的最终结果是1111001011，这里负值符号是延伸的。

（ii）1*001011=001011

（iii）1*001011=001011

（iv）增加00001作为这3个组合的否定纠错。

1111110100也作为负值符号的延伸。

001011

001011

00001这里作为负值的否定纠错。

0011010001这里我们不再使用高位。

C. 基-8

在基-8 Booth乘法器中我们把4位作为一组[34]。

每个组被编码为一个有符号的数字，如表Ⅲ

表Ⅲ

基-8 Booth编码乘数[8][17]

groups

Partial products

0000

0

0001

1

0010

1

0011

2

0100

2

0101<!--

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[152778]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章