
英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
使用约束NewWave方法分析自升式单元
M.J.Cassidya, R.Eatock Taylorb, G.T.Houlsbyb
Centre for Offshore Foundation Systems, University of Western Australia, Crawley, WA 6009 Australia Department of Engineering Science, Oxford University, UK
摘要:
随着海洋石油开发力度的加大,在较深水和恶劣环境中使用自升式装置的需求不断增加。在这些环境中,我们需要对自升式装置发生的物理过程进行准确的分析。本文主要研究适用于自升式动态评估的模型。在结构的考虑上,我们在基础和波浪荷载的非线性方面采取了平衡的方法。基础模型使用开钻密封罐的加工硬化塑性模型。 使用NewWave理论考虑波载荷的光谱含量,并通过约束,显示随机波历史的重要性,在一个完全随机的背景下研究NewWaves理论。 本文详细介绍了使用约束NewWaves确定海洋状态的短期极端反应统计的方法。copy;2001 Elsevier Science Ltd.保留所有权利。
关键词:NewWave;约束NewWave;升高; 升高基础;加工硬化可塑性; 随机波
1,介绍
由于自升式单元大多数用于在深度达120米的海上钻井作业中,它们在海上石油工业中具有重要的经济意义。自从第一次在墨西哥湾相对较浅的部分应用以来,在更深的水域和更恶劣的环境中使用的需求一直在不断增加[1]。还有一个实际需求就是希望能在一个地方长期承担自升式作业,特别是在实际生产中[2]。
在一个给定的水域运行之前,通常必须要对这个地方50年的风暴、波浪等进行评估。在过去,由于是在相对较浅和平静的水域中作业,对于这一评估事项,可能我们会使用过于简单和保守的分析技术。然而,随着在越来越深的环境中升降,我们越来越需要了解更多的自升式行为并开发对应的分析技术。 “移动式起重机组现场指标评估指南”[3]的出版就是海上工业要求规范和制定自升式评估程序愿望的一个例子。
自升式建模中最重要的地方是在:
1动态效果,
2几何等非线性结构建模,
3环境波浪载荷,
4基础响应模型。
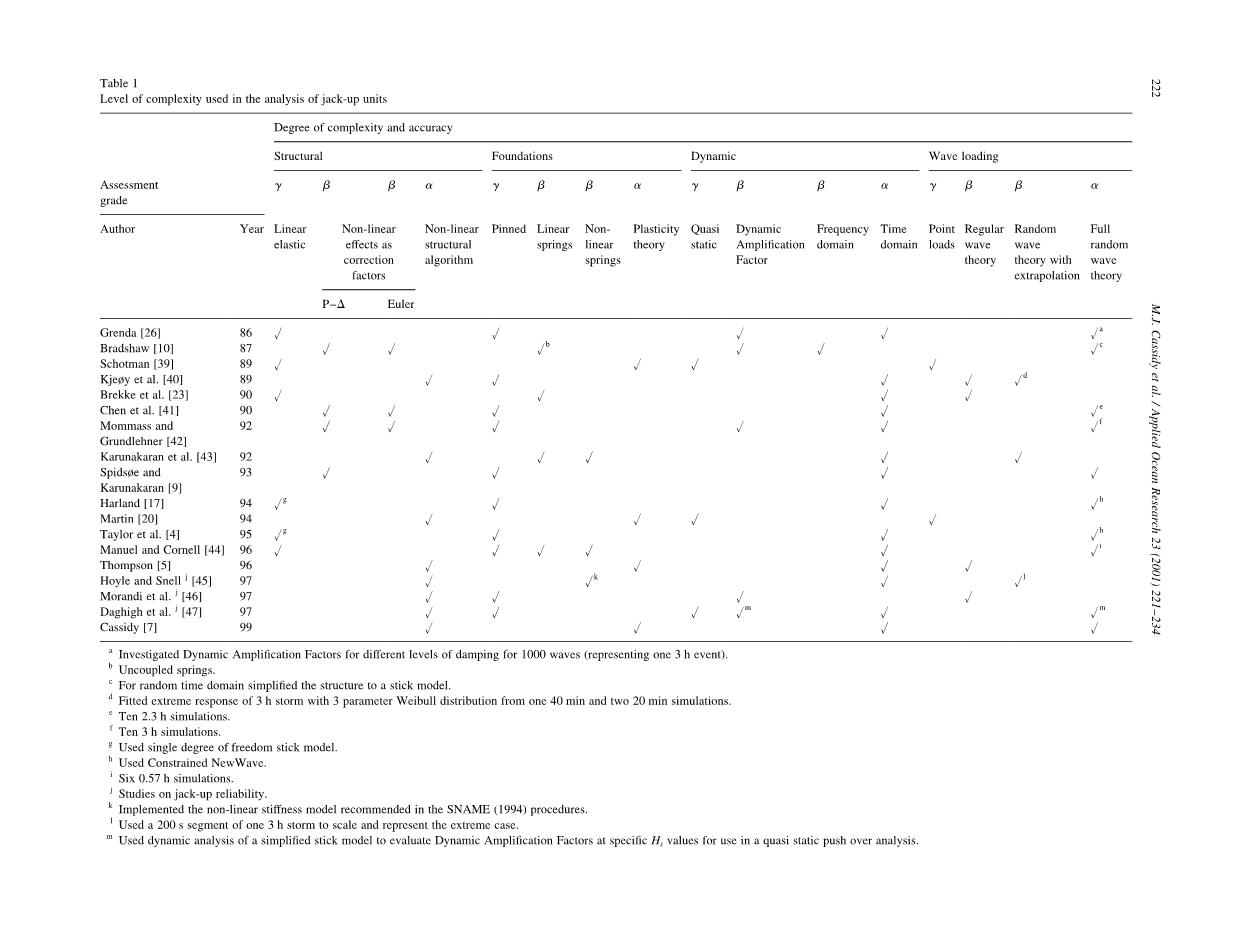
到目前为止,这种发展已经具有相当的多样性,我们开始研究根据不同环境的复杂性来进行不同的分析。表1详细介绍了过去15年来发表的一系列研究成果。我们可以看出,在突出的四个发展领域已经被分解成越来越复杂(和准确)的组成部分。表1显示,单一研究通常在一个或两个领域采用复杂的研究方法,但在其他方面使用最简单的假设。对于基础建模来说,尤其如此。许多研究使用详细的结构模型或先进的波浪力学,但同时仍然使用最简单的基础假设(即固定基础)。
在计算自升式确定性常规波理论的波载荷时,如艾里和斯托克斯,以及莫里森方程仍然广泛使用。 然而,我们假设所有的波能集中在一个频率分量,但却不在实际海洋环境的广谱范围内,常规波理论给出了无代表性的动态响应。对于作为动态响应的自升式结构,重要的是模拟海洋装载过程中的随机性,光谱和非线性特性。极端的动态响应不仅取决于当前正在应用的负载,而且还受其负载历史的影响。因此,最准确的估计极端反应的方法是基于伪随机性海洋表面的时域模拟和相应运动学的计算。
然而,在随机时域仿真结果中获取相关信息在计算上是耗时的,每个时间序列中只有几个波浪能够产生极端的结果。因此,表1中的大多数研究是使用简化假设。与此相反,通过在任意随机时间序列中约束具有预定大峰的NewWave,可以设计出一种计算极度统计量而不具有相同程度的计算负担的方法[4]。
本文的目的是双重的。 首先,我们将提出一种对自升式平台的建模来说更为平衡的方法。使用动态结构分析程序(称为jakup)来考虑自升式平台分析中的主要非线性。在本文中给出了jakup中使用的结构、基础和波浪荷载模型的主要特征。更多细节可以在Thompson [5],Williams[6]和Cassidy [7]等人发表的论文中找到。其次,概述了使用约束NewWaves来评估自升式单位的极端反应统计的方法。并展示出了遭受短期(三小时)风暴的自升式单元的示例数值计算。
2,使用的模型大纲
2.1 示例结构
图1为本文中使用的理想平面框架自升式的示意图。 平均水深假定为90米,图1所示是在严酷的北海条件下使用的三柱式自升式的钻机典型尺寸。图1表示等效梁模型,图1中标出了相应的梁的刚度和质量。船体表现为具有刚性腿/船体连接的梁元件。尽管腿部/船体顶棚的非线性被认为是重要的[8,9],但由于钻机和钻机的不同,所以非线性在很大程度上取决于腿顶和锁定机构的细节。这些非线性的精确建模可以涉及使用特殊元素建模间隙效应(参见参考文[10])。 没有尝试在这项研究中纳入这些影响。腿段的结构节点位置和流体力学建模系统的示例如图1所示。
2.2 波浪载荷模型
NewWave理论和约束NewWave已经在jakup中实现,用来评估表面高程和波动态,扩展Morison方程用于计算包含自升式腿上的流体动力学负载的相对运动。在未被检测到的波束位置上计算水平粒子运动,并通过将分布负载与对应的形状函数(使用高斯积分)进行积分,从而得到等效节点载荷。
NewWave理论,由Tromans等人描述的确定性方法 [11]。通过假设表面高程可以被建模为高斯随机过程,可以从理论上推导极端事件(例如峰顶)处的预期高程。这个极端事件周围的地面高程是由与其发生相关的统计学上最可能的形状建模的。考虑到海洋的光谱组成,可以用作长时间历史的常规波和全随机时域模拟的替代。
作为时间的函数,表面高程可以是写成:
(1)式中tau;=t-t1是相对于峰顶的初始位置的时间(即t1是极端事件发生的时间)。在等式 (1)中,(1)描述了最可能的值,其中a是波峰高度为波峰最大值时和平均水位之间的垂直距离,r(tau;)为海面高程的自相关函数。自相关函数与表面能谱的傅里叶逆变换成正比,从而可以有效地确定表面高程。
方程式(2)相对于(1)式来说是一个平均为零的非平稳高斯过程,表示从顶部的零增加到距离顶点一定距离处的底层海洋的标准偏差。因此,随着波峰高度的增加,术语(1)成为主导,可以单独用于导出峰顶附近的表面高程和波运动学。
连续时间自相关函数被定义为:
在tau;=0周围,R(tau;)随着极端波群的时间成比例; 对于t = 0的时滞,方程的自相关函数 (2)减少到1,使得有效缩小NewWave的表面仰角,得到平滑的曲线。见下面的等式(3)。
通过自相关函数(等式(1))确定的NewWave形状,可以通过(N)个分量正弦波进行离散化处理。由于波数与频率之间存在着独特的关系,也可以包含空间依赖关系,可以得到离散形式:
其中,kn是第n个分量的波数。 (在Newman [12]中,我们已经在jakup中得到在恒定水深下的平面波的色散关系的近似求解方法。)如以前所述,a是峰顶,Seta;eta;表面高程和s对应于该波谱的标准偏差。X=x-x1是相对于初始位置的距离,X=0代表波峰。这就允许在空间中定位时,使得峰位可以处于用户理想中的定位位置,这是用于时域分析的有用工具。
NewWave的这一确定性方法使得它可以方便地并且被有效地实现到诸jakup的结构分析程序中。此外,由于是基于线性理论,一旦知道了将要作业的目标水域,就可以很容易地知道该地水波粒子的运动。然而,我们通常必须注意在使用的多种拉伸方法的波峰中描述它们的值。这些包括Delta拉伸[13]和Wheeler拉伸[14]。尽管在文献中描述了许多其它的拉伸或外推方法,但是没有明确的优选方案。由于自升式腿的实质性分离,因此在两个空间位置上精确地评估表面仰角和运动学是重要的。 NewWave理论为正规波浪理论提供了一个现实的具有确定性的替代方案。
对于静态响应的结构,NewWave理论已经成功地用于预测全局[15]。它也已经在Elzinga和Tromans [16]中的实际平台上测量的全局负载和常规随机波模型进行了验证。然而,当用作分析动态敏感结构的时间历史时,NewWave的单一项目不足以发现大峰值的海洋的随机性,因此该随机性会影响到结构的动态响应。通过在完全随机的背景下约束具有预定高度的NewWave,NewWave理论可用于产生随机曲面高程的时间序列。这以数学上严格的方式进行,使得约束序列在统计学上与原始随机序列无法区分。Tayloret al概述了实现此目的的细节[4]。
图2表示了以Hs= 12m和Tz =10s为特征的随机海况,嵌入具有15m的波峰高度的NewWave的表面高程:波被约束,使得其峰值出现在约60s处。如图2所示。在这个例子中,NewWave在表面高程上的影响包含在约束峰值的40秒以内。
约束NewWave理论使其对极端反应统计量进行简单和高效的评估,条件是所需的极端反应与随机海域内的大波浪的发生相关。Harland [17]和Harland [18]等人已经使用NewWave计算极值。约束NewWave在自升式响应研究中的应用在此进一步讨论。
2.3 结构模型
结构非线性(P-△和欧拉效应)通过使用Oran[19]的梁列理论的路径依赖公式来确定增量刚度矩阵。另外由于存在剪切而在梁上产生额外的端点旋转的修改也已经实现[20]。质量和阻尼矩阵都是时间不变的,前者使用立方Hermitian多项式形状函数,后者通过使用瑞利阻尼。结构阻尼系数被定义为最低两种模式,并被设置为临界值的2%。这表示基于测量自升式的估计采用瑞利阻尼的典型值[21,22]。例如,Brekke等人[23] 估计在约70米的水中的自升式单元的结构阻尼位于1.8至2.8%之间。
通常,自升式评估使用与其结构相同的准静态分析方法[24]。然而,我们得考虑到动态效应的需要[10,25,26]。随着在更深的水中使用,动力效应对总响应的贡献变得越来越重要,因为自升式的自然时期接近海域的高峰期。由于它们能够对所有非线性进行建模,所以使用数字逐步直接集成的时域技术为分析自升式的极端反应提供了最通用的方法。在jakup中,取beta;=0.25;delta;=0.5,因为它是一种无条件稳定和高精度的算法。在Martin [20]和Thompson [5]中可以找到结构配方和动态解决方案技术的进一步细节。
2.4 基础模型
硬化塑性理论的应用被认为是用数学分析术语来模拟土壤行为的最佳方法。 这是因为基础的反应纯粹是以强制结果来表达的。考虑到都处于一个水平基础上,所以提高了关键零部件压力(通常在腿部/船体连接处)和其他关键响应值[27,28]。此外,自升式的运动时间也减少了,通常能改善了钻机的动态特性。
Jakup具有将螺钉、螺纹或线性弹簧建模为自升式基础的能力。 此外,已经开发了用于密砂的斯普达坎基的应变硬化塑性模型,并且其数值公式被实现为jakup。它被称为C型,其主要特征在这里进一步讨论,然而,为了详细的描述,可以参考Cassidy [7]。 ModelCis基于在牛津大学进行的一系列实验测试,并在Gottardi[29]中论述。并遵循“模型B”,Martin [20]描述的应变硬化塑性模型,适用于粘土上的泥沙。
C模型有四大部分:
(1)三维垂直,力矩和水平载荷在空间中的屈服面的经验表达式(V,M /2R,H)(注意:力矩为spudcan的直径,2R)。该包络线表示允许负载状态的屈服轨迹,其“橄榄球”形表面如图3所示。该形状描述为在恒定V平面上的截面中的偏心椭圆,并且在包括V轴的任何部分上近似抛物线形。一旦表面变量建立,该表面内的任何负载变化将仅导致弹性变形。然而,当负载接触到表面时,可能会导致塑性变形。
(2)经验应变硬化表达式,用垂直位移的塑性成分确定屈服面的尺寸变化。 虽然屈服面的形状被认为是恒定的,但是随着垂直塑性穿透(当基础被进一步推入土壤中时)膨胀。通过将圆形基础的实验观察结果与圆锥形基础理论预测结合起来,可以得出用于混凝土的应变硬化规律。这个“组合”应变硬化规律的细节不在这里,但可以在Cassidy [7]或Cassidy和Houlsby [30]中找到。
(3)屈服面内弹性载荷 - 位移行为模型。 有限元工作表明,水平和旋转基脚位移之间存在交叉耦合[33],其形式为线性弹性增量力 - 位移关系:
其中w,theta;和u分别是垂直,旋转和水平位移。G是一个代表性的土体剪切模量,计算方法为:
其中pa是大气压力,gamma;rsquo;是浸没的单位重量的砂,g是无量纲剪切模量因子式。(4)代表了具有典型的刚度kv值的C型弹性特性;Kv;Km;Kh;Kc和g在表2中给出。
(4)允许在产量期间预测基脚位移。实验证据不支持相关联的应用,并且塑性势函数g被定义为涉及塑性位移之间的比率。详细信息在Cassidy [7]中
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[139932],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


