
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
双台起重机在平面运动均布质量载荷中的动力学与控制
摘要:操作者指令引起的有害振动降低了有效操作速度并且降低了双起重机移动时均布质量载荷的安全性。因此,越来越多的工作投入到双台起重机的动力学和控制研究中。然而,很少有研究致力于精确的估算固有频率,尽管这是双起重机控制的一个重要因素。本文提出一种新的方法来预测有不同缆绳长度双平面起重机的固有频率。另外,还提出了一种改进的非常不敏感的(MEI)输入整形器来抑制双起重机有效载荷摇摆和俯仰的振动。MEI式整形器对很大的频率变化有很强的稳健性,并且在急动限制下具有良好的性能。通过对小型细长梁式双起重机进行了仿真和试验研究,验证了该系统的动态特性和MEI式整形器的有效性。
关键词:双起重机 均布质量 横梁 动力学 振动控制
1.引言
多台起重机吊运大型载荷这种方式在世界各地的建筑、运输和制造业中应用广泛。[1-9]值得注意的是,多台起重机通过悬索将悬挂载荷固定的方式创造了一种灵活多变的结构,这降低了工作速度、效率和安全性。操作员的命令行为和外部干扰都将引起大型载荷法的有害震荡。因此,有必要研究多台起重机吊运均布质量载荷的动力学与控制,以确保安全和有效操作来说是十分重要的。
先前文献[10-18]已经讨论了多台起重机吊运大型载荷的动力学模型。该系统比具有大型载荷动力学以及双摆动力学典型单台起重机要复杂的多。[19-31]对吊运大型载荷的多台起重机的固有频率进行评估和分析是具有挑战性的。在文献中对每根缆绳的两个频率取平均值来预测系统的频率。[13-15]然而,只有在两根缆绳长度相同时取平均频率才是正确的。此外文献[18]通过假设两个缆绳长度相同来估计双起重机的平衡点。可是,在实际的工作条件下缆绳长度是不同的。
通过大量实例,给出了多台起重机吊运大型载荷时抑制振动的解决方案。这种方法主要集中于开环控制,它修改操纵指令以驱动多台起动机进行低摆幅运动。Leban等人提出了一种用于限制双起重机吊运时摆动的逆运动学控制器。在小型双台起重机上证明了逆运动学控制器的有效性。[10]Perig等人提出了移动双台起重机摆动最低的最优控制办法。他们通过模拟横梁传输证实了这种方法的可行性。[11]不幸的是,这种动态计算负荷是逆运动学的应用和最优控制方法的讨论中的障碍。[10,11]
输入整形器包含一系列的脉冲,它通过卷积命令来减少载荷的摆动。以前展现的输入整形器包括零振动(ZV)整形器,零振动类(ZVD)整形器,极不灵敏(EI)输入整形器,指定不敏感型(SI)整形器。这些输入整形器在频率和阻尼方面展现出良好的不敏感性。因此它们已经被成功的应用于许多可变结构类型中,但是这种技术不能防止外部干扰。[32-34]
文献[12-17]已经证实了这种输入整形器在双台起重机上的可行性。实际上,输入整形器依赖于对固有频率的准确估计,而很少有人注意到这一点。因此,频率估计是输入整形技术的一个障碍。Lu等人提出了一个双起重机的反馈控制[18]。然而,这个研究结果只有在悬索长度相同的情况下才有效。
本文的贡献有两个方面:1)本文提出了了一种计算两台起重机吊运均布质量梁时的方法。该方法能很好的预测在大缆绳比率情况下的频率。2)提出了一种MEI式整形器,用于控制双起重机的振动。MEI式整形器对频率建模误差有良好的稳健性。另外,MEI式整形器有良好的的冲击限制特点,这有益于执行器追踪成形指令,并且抑制了系统的非线性和不确定性。MEI式整形器也有可能应用于其他类型的机械,包括协作机械手。
本文其余部分安排如下。第二节提出了两台起重机吊运均布质量梁模型。动力学分析也在这节中提出。第三节介绍了用于控制双台起重机的MEI式整形器,并对整形器的稳健性和有效性进行了数值验证。第四节的实验证明了双台起重机的动态特性和稳健性。第五节提出结论。
2.吊运均布质量梁的双起重机的建模和动力学研究
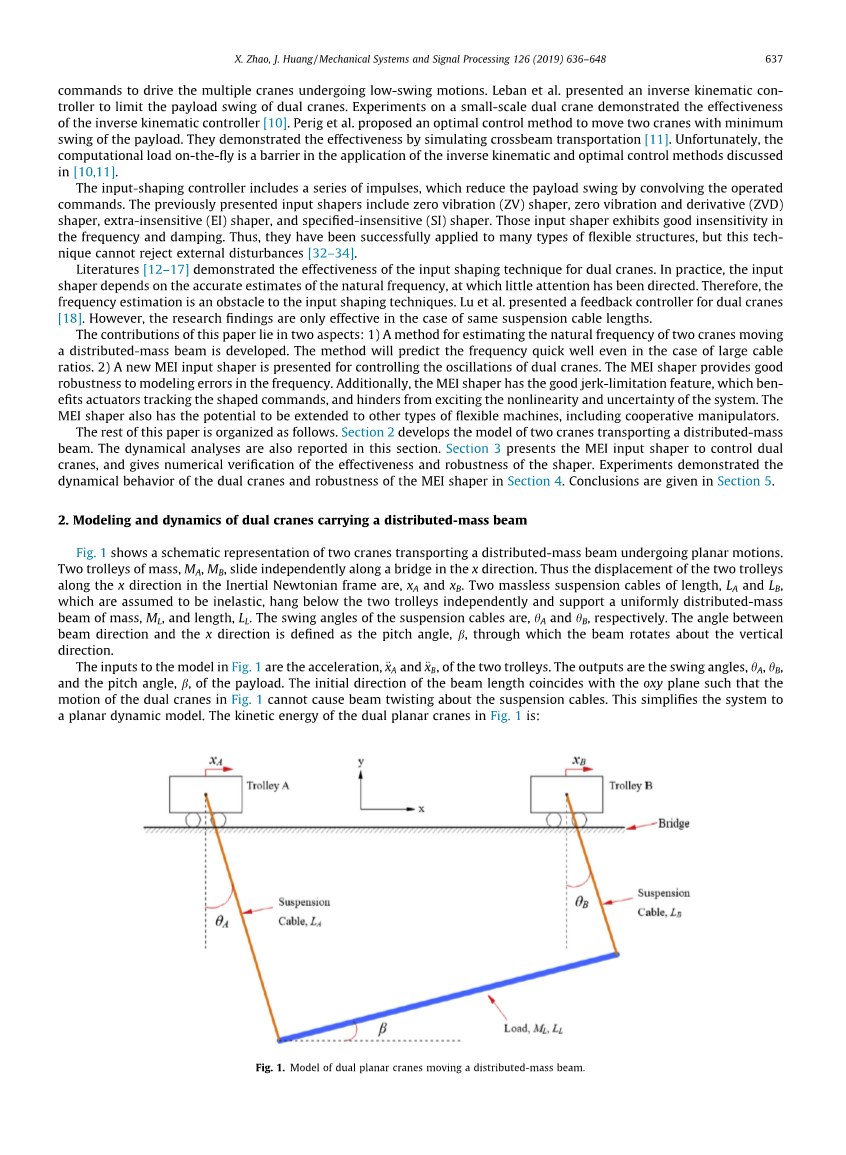
图一是两台起重机在平面内吊运均布质量梁的示意图。两辆小车,,,沿着一个梁向chi;方向移动。因此两个小车在牛顿惯性系中沿chi;方向的位移为,两条长度为和的无质量悬索(假定为非弹性悬索)独立悬挂在两个手推车下方,并支撑质量为ML和长度为LL的均布质量梁。悬索的摆角分别为和。悬索方向和chi;方向之间的角度被定义为俯仰角beta;,悬索绕垂直方向旋转。
图1中模型的输入是两个小车的加速度,和。输出是有效载荷的摆角、和俯仰角beta;。梁长度的初始方向与oxy平面一致,因此图1中的双起重机的运动不会导致梁绕悬索扭曲,因此图1中的双起重机的运动不会导致梁绕悬索扭曲。这将系统简化为平面动力学模型。图1中双平面起重机的动能为:
图表 1双台起重机吊运均布质量梁的动力学模型
(1)
假定小车质心为零势能面双平面起重机平面的势能为:
(2)
然后利用广义拉格朗日方法,将图1所示模型的非线性运动方程导出为:
(3)
,
, (4)
, (5)
其中g是重力常数,根据动力学模型(3)-(5),计算平衡角的约束条件如下:
, (6)
其中、、分别是摆角的平衡角、摆角和俯仰角。通过假定平衡角(6)附近的振荡,可从动力学模型(3)-(5)导出线性化模型。
根据线性化模型,得到了双平面起重机的固有频率方程:
, (7)
其中omega;是双平面起重机的固有频率,系数、、、在附录中给出。固有频率的封闭形式是引起争议的。相反,求解式(7)得到了固有频率的数值解。式(7)有三个解,包括一个频率和另两个零解。由于子系统(4)和(5)的刚度均为零,因此出现两个零解。
式(7)得出的固有频率取决于小车距离、悬索长度和载荷长度。图2a显示了固有频率与小车距离的函数关系,当悬索长度,悬索长度,,和梁长度,,分别为82cm、64cm、120cm。在25cm前,随着小车移动距离的增加,固有频率增加。在这一点之后,固有频率降低 。图2b示出当小车距离、悬索长度和梁长度分别固定在120cm、64cm和120cm时,不同悬索长度的自然频率。自振频率在120cm前随悬垂长度的增加而急剧下降,然后略有增加。图2c示出了当小车距离、悬索长度和悬索长度分别固定在120cm、82cm和64cm时,由不同梁长引起的固有频率。极小值出现在有效载荷长度125厘米处。载荷长度的微小变化导致固有频率的较大变化。图2表明,固有频率随着小车距离的变化而略有变化,并且随着有效载荷长度和悬索长度的变化而变化。
用于驱动模型(3)-(5)的命令是梯形速度剖面 [32]。两种手推车之间的初始距离、最大驱动速度和最大驱动加速度分别固定在120cm、20cm/s和2 m/。图3a示出当悬索长度悬索长度和梁长度分别为82 cm、64 cm和120 cm时,由小车A的不同行驶距离引起的峰间残余振幅[32],摆动角和俯仰角的峰值是由小车加速和减速引起的振荡之间的构造性干扰引起的。
图2.固有频率与系统参数。(a) 小车距离;(b)悬索长度;(c)有效载荷长度
摆动角和俯仰角的峰值是由小车加速和减速引起的振荡之间的构造性干扰引起的。这两种振荡有时同相,有时不同相,从而分别产生波峰和波谷。波峰与波谷之间的距离与系统的固有频率相对应,可使用式(7)的数值解来估计。此外,随着行驶距离的增加,摇摆角、和俯仰角beta;的峰值幅度增大。因此,减小载荷摆动会使载荷俯仰产生小的振荡。
图3b显示出了当行驶距离、悬索长度和横梁长度分别固定在20cm、64cm和120cm时,用于改变悬索长度的模拟残余振幅。在29cm前,摆角的残余振幅随悬索长度的增大而增大。在这一点之后,它会随着悬索长度的增加而减小。在60cm前,摆角残余振幅随悬索长度的增大而增大,之后摆角残余振幅减小。在悬索长度50cm的处,为俯仰角beta;的极大值,在悬索长度为130cm时,俯仰角中的残余振荡近似为零。在这种情况下,载荷俯仰中的近零振荡是由摆动的零平衡角、引起的。零平衡角和导致两条悬索摆动之间的分离效应。
图3c示出了当行驶距离、悬索长度和悬索长度分别固定在20cm、82cm和64cm时,作为有效载荷长度的函数的剩余振幅模型。在这种情况下,由于摆动为零,摆动节距中的最小值出现在的梁长度为30 cm处。载荷中的另一个零振荡点出现在横梁长度为101厘米处。
图3.载荷摆动和俯仰的剩余振幅模型。(a)行驶距离;(b)悬索长度;(c)载荷长度。
这也是因为摆动的平衡角和在这一点上都被限制为零。因此,系统的动力学特性是(6)中平衡角和(7)中固有频率干涉的结果。
3.双起重机控制
本节将介绍极不敏感(EI)输入整形器和改进的极不敏感(MEI)输入整形器。原始驱动命令通过整形器过滤以创建整形后的命令,这使得可以在最小的载荷振动移动双平面起重机。
3.1 EI整形器
EI整形器对频率中的建模误差提供了最有效的鲁棒性[34]。无阻尼系统的EI整形器为[33]:
, (8)
其中是振动的承受能力,
, (9)
omega;是固有频率,是阻尼比。对于阻尼系统,EI整形的形式为[33]:
, (10)
其中,
,(11)
, (12)
, (13)
零阻尼EI整形器的频率灵敏度曲线如图4所示。频率为5%的整形器不敏感范围从0.801到1.199。EI整形器在设计频率下抑制低于承受能力的残余振动,并在将附近的两个频率残余振动限制为零。
EI整形器脉冲的最大振幅约为0.5。双机驱动时,0.5的脉冲幅度较大。这可能会导致巨大的冲击,阻止跟踪执行器的形状指令,并激发双起重机的不确定性或非线性。因此,有必要发明一种改进的EI整形器,其具有与EI整形器相似的上升时间和频率不敏感性,但具有较低的脉冲幅度。
3.2 MEI式整形器
在平衡角附近的模型子系统(3)可以近似为具有式(7)中给出的固有频率的非耦合二阶系统,而子系统(4)-(5)可以近似为两个零刚度系统。由一系列k脉冲产生的具有固有频率omega;和阻尼比xi;的二阶系统的谐波响应为:
, (14)
其中和是MEI整形器的第k个脉冲幅度和时间。相应的振幅由下式给出:
, (15)
其中
, (16)
图4.MEI和整形器的频率灵敏度曲线。
(17)
令方程(16)和(17)为0得到脉冲序列和的解,它们与操作员命令卷积,然后以零振荡移动小车。然而,实际系统中存在一定程度的不确定性或非线性,因此将残余振荡限制在零是一个挑战。因此,设计频率下的剩余振幅可以限制在承受能力以下,[33]:
, (18)
其中是MEI整形器的持续时间。为了提高设计频率附近的鲁棒性,应将两个附近频率和处的剩余振荡限制在零[33]:
, (19)
, (20), (21)
, (22)
脉冲的总和应限制在一个,以便MEI形命令达到与操作员命令相同的设定点:
, (23)
注意,持续时间约为阻尼振动周期。强迫残余振动对频率的导数为零,应增加对频率建模误差的鲁棒性:
, (24)
将式(24)代入式(18)和式(27)可得到修正系数p和q的数值解。当振动的控制水平设为5%时,无阻尼系统修正系数的解为p=0.8584和q=1.1429。
图4还示出了为零阻尼设计的频率灵敏度曲线。图4还示出了为零阻尼设计的频率灵敏度曲线。MEI整形器产生陷波滤波果。成形器将附近频率和处的残余振动消除为零,并将残余振动限制在设计频率omega;的承受能力以下。MEI整形器的频率灵敏度曲线范围为0.798~1.205,低于5%的振动水平。因此,MEI整形器抑制广泛的系统频率。此外,阻尼比的变化对MEI成形器的振动影响不大。这个结论是良好的,因为在实际情况下准确估计阻尼比通常是很难的。
此外,MEI整形器的最大震级约为0.25。因此,MEI成形器在冲击极限下具有更好的性能,有利于跟踪执行器的成形指令,防止系统的不确定性或非线性。总的来说,MEI整形器比EI整形器具有更好的冲动限制特性,而MEI整形器和EI整形器具有相似的频率不敏感度和上升时间。
3.3 模拟结果
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[237112],资料为PDF文档或Word文档,PDF文档可免费转换为Word


