
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
快速匹配法铺丝轨迹定义
摘要:我们来研究将移动接口的数值模拟效率应用于定义复合结构的纤维铺放轨迹的方法。这种基于快速匹配法的适应性的新方法具有两个优点。首先,它通过生产等距纤维进程来模拟自动纤维铺放机器的机制,在这种纤维进程中没有没有不良的差距或重叠。其次,它可以直接在网格上而不是通过几何方程来处理复杂的曲面。这种方法已经由真实的案例研究和弯曲的纤维轨迹论证了。
1.介绍
在自动化纤维铺放技术(AFP)或自动牵引位置(ATP)技术中,机器的头部安置多个不同形状的浸染纤维。正如所报道的,在机器头部的一个进程中,AFP的机器头可以同时并排牵引32条纤维。通过连续的铺放进程可以获得完整厚度的层。在[2]中提供了对纤维进程的不同方法的描述。AFP机器对于自动纤维铺放进程的优势是它允许使用窄的单个纤维束来定义弯曲的纤维路径。因此AFP机器可以处理带有非直线纤维进程的复杂形状的结构。
织物的覆盖模拟已经被广泛研究了。 例如,在[4,5]中,纬纱和卷绕方向通过计算纤维的交叉点来定义。这些点在每个方向上都有固定的间距并在覆盖表面上构成了网格。纤维是连接交叉点的折线。AFP仅对纤维轨迹的计算机定义进行了少量研究。Hyer和Gurdal在[7-10]中是第一批为平板中可变刚度层压板提供计算机基础解决方案的作者。就AFP的轨迹而言,用于定义弯曲纤维的方法具有在覆盖表面上进行纤维取向的功能。在[11]中,纤维被铺放在平坦的表面上,并被假定为一组贝塞尔曲线或多项式函数。在[2,10,12]中,纤维被定义为测地线,恒定角度路径,具有线性变化的纤维角的路径或具有恒定曲率的路径。它们已经被应用于锥体和圆柱体。[13-15]中的第三种方法是考虑在覆盖表面上的参考曲线,并计算表面上与参考曲线有着恒定距离的点的集合。纤维是连接这些等距点的折线。所有这些方法都存在着两个主要的缺点。首先,它们都是需要覆盖表面参数方程的几何方法。而在大多数工业情况下,这些参数方程并不是可用的。通常,使用CAD软件来定义覆盖表面。因此,需要一种使用网格而不是参数方程定义弯曲纤维的方法。其次,这些方法(第三种除外)不会在AFP程序中的进程产生等距离的路径。如果两个连续路径的中心线不等距,就会出现不需要的缝隙和重叠(见图1)。这些缝隙使结构变得脆弱并且这些重叠增加了重量。在[2]中提到使用AFP机器的切割和重新启动功能允许避免不需要的间隙和重叠,从而在结构上提供恒定厚度的层。然而这种技术是昂贵的,因为不能使用机器所提供的恒定(和最大)宽度进程的全部能力。
在本文中,提出了一种称为快速匹配法(FMM)的数值方法来定义一般(可能复杂)几何的表面上的等距线。快速匹配法用于物理学上模拟移动接口的很多领域。这里开发的方法依赖于参考曲线结构的定义,该参考曲线表示界面的初始位置,可以看作是由纤维进程中心线表示的初始纤维轨迹。该参考曲线从现在开始称为“参考纤维”。然后该参考纤维在整个表面上铺放,使得(可能)弯曲的纤维轨迹产生,但不存在间隙和重叠的缺点。此外,这种方法与表面的网格协调工作,而不是使用参数方程来定义结构的几何形状。这一特性使得可以去定义复杂几何结构中的纤维轨迹。最后,最后,由于该方法在网格的每个元素中提供局部纤维取向,所以当复合元件必须进行结构分析时,要必须进行有限元法的自然输入[17]。
本文的结构如下。在第2节中,介绍了移动界面仿真的一般数学公式和本文提出的方法。在第3节中,介绍了针对参考纤维定义开发的算法。第4和第5节集中介绍使用标准FMM方法使这种初始信息在整个表面上铺放。在第6节中,为了处理定义合适的等距纤维轨迹的具体问题,对FMM进行了若干调整。在第7节中,解释在表示表面的网格的每个元素中如何获得局部纤维取向。最后,第8节提出了一组数值实验,以显示新方法的效率。它包含了具有直的和弯曲的参考纤维的平面和非平面复杂结构的情况。
等距 间隙 重叠
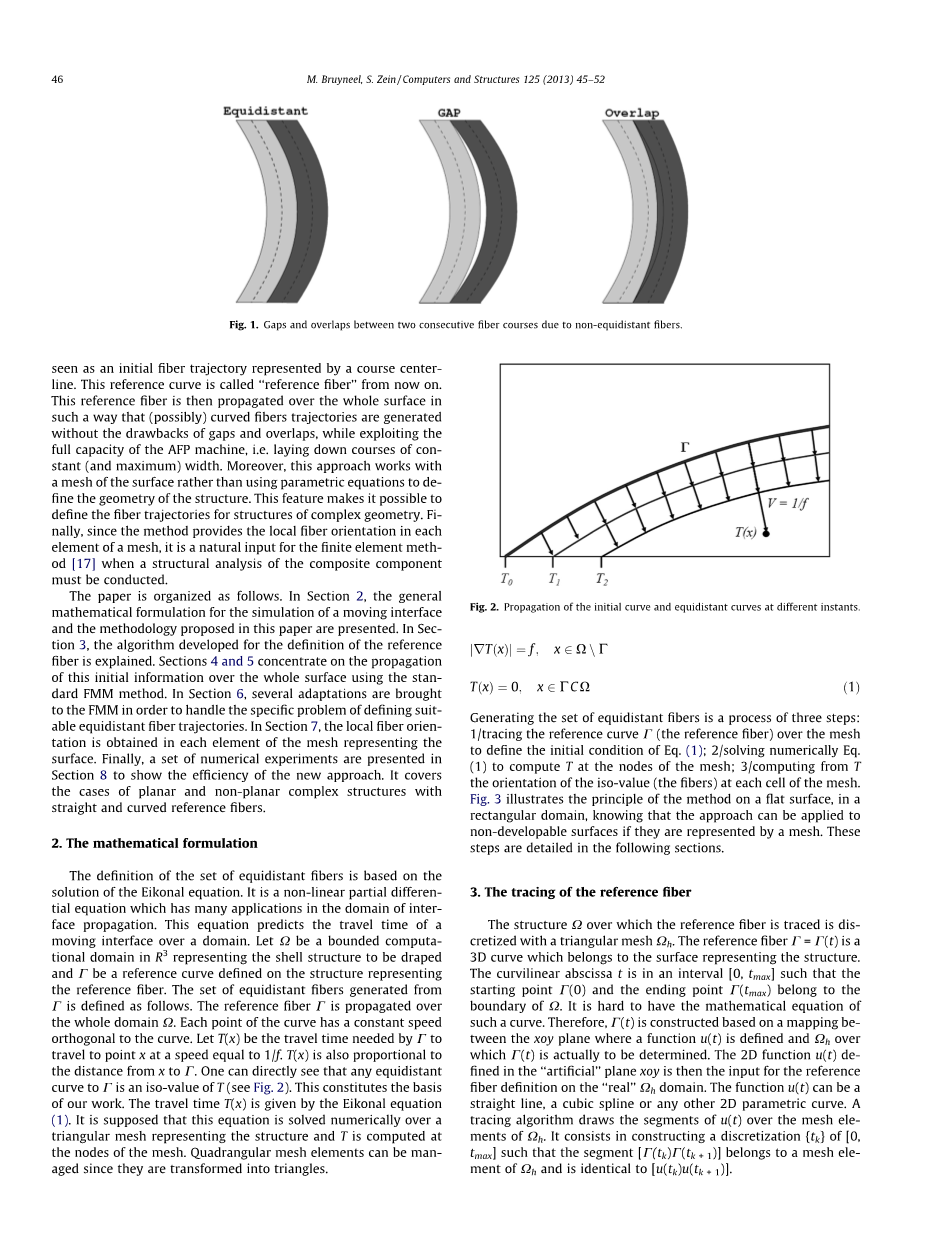
图1.由于非等距纤维所造成的间隙和重叠
- 数学公式
等距纤维集的定义基于Eikonal方程的解。它是一种非线性偏微分方程,在接口铺放领域有许多应用。该方程式预测移动接口在域上的行进时间。令X是R3中的有界计算域,表示要覆盖的表面结构,C是在表示参考纤维在结构上定义的参考曲线。由C产生的等距纤维集合定义如下。参考纤维C在整个域X上铺放。曲线的每一点具有与曲线正交的恒定速度。令T(x)是C以等于1 / f的速度行进到点x所需的行进时间。T(x)也成正比从x到C的距离。可以直接看到C的任何等距曲线是T的等值(见图2)。这构成了我们工作的基础。铺放时间T(x)由Eikonal方程(1)给出。假设这个方程是通过表示结构的三角形网格数值求解的,并且在网格的节点处计算T。这也可以计算四边形网格元素,因为它们被转换为三角形。生成等距离纤维的集合是三个步骤的过程:1 /通过网格跟踪参考曲线C(参考纤维)来定义等式(1)的初始条件; 2/解方程 (1)的数值来计算网格的节点处T;3 /从T计算网格上的每个单元格处的等值(纤维)的取向。图3示论证了在矩形域中平坦表面上的该方法的原理,可以看出如果该方法可以由网格表示,则该方法可以应用于不可展开的表面。以下部分将详细介绍这些步骤。
图2.在不同的瞬间铺放的初始曲线和等距曲线
(1)
图3.方法的步骤:(a)定义网格结构(b)追踪参考纤维(c)求解程函方程(d)计算纤维取向
3、参考纤维轨迹的追踪
使用三角形网格Xh将跟踪参考纤维的结构X离散化。参考纤维C = C(t)是属于表示结构表面的3D曲线。曲线横坐标t处于[0,tmax]区域间,使起点C(0)和结束点C(tmax)属于X的边界。但很难有这样一个曲线的数学方程。因此,C(t)是基于定义函数u(t)的xoy平面与Xh之间的映射来构造的。在“人造”平面xoy中定义的2D函数u(t)为了定义参考曲线而被输入在真实”Xh域上。函数u(t)可以是直线,三次样条或任何其他二维参数曲线。一个跟踪算法在Xh的网格元素上绘制u(t)的段。它包括构造[0,tmax]的离散化{tk},使得段[C(tk)C(tk 1)]属于Xh的网格元素,并且与[u(tk)u(tk) 1)]是一样的。
在这一段,使用以下符号。大写字母中的顶点是包含结构的3D空间中的点,小写中的顶点是位于xoy平面中的点。
Xh中的每个元素ABC被映射到已知u(t)的平面xoy中的相同三角形abc里。abc中u(t)的定义报告给Xh的等价三角形ABC。让我们假设u(t)从ab进入abc(见图4)。
在初始化步骤中,假设u(0)在xoy轴的原点。 C(0),网格Xh上的C的起始点定义如下:(1)C(0)在边缘AB上;(2)C(t)进入到元素ABC中;(3)C(0)分割AB的比率k1使AO向量等于k1倍的AB向量。在迭代k = 0时,三角形ABC在平面xoy中映射到abc中(图4)。顶点a和b在y轴上定义使得ao向量等于k1倍的ab向量。让我们取tk = 0。在每次迭代k中,在平面xoy中构造与网格元素ABC相同的三角形abc,以便u(t)进入abc,这样u(t)输入adc就能使t大于等于tk。abc的边缘ij(不同于ab)由u(t)中tgt;=tk所决定。它可以是ac或者bc。在图4的示例中边缘是bc。然后,通过计算h除以ij的比率k2,获得边ij上的交点h = u(tk 1)。它来自于ih=kij。通过向后映射使abc变成ABC并且ij变成IJ,C(t)在IJ上的出口点H应满足IH等于k2倍的IJ。
迭代k处的出口顶点IJ是迭代k 1处的入口边缘AB(见图5)。然后确定C(t)上将进入的Xh上的下一个元素。这个新元素被称为ABC,使得AB是IJ,k1 = k2和k = k 1。如果这个新元素不存在,则tmax = - tk 1,并且算法被停止。否则就执行新的迭代像图5中所举例的那样。
如果纤维达到一个顶点,则k2=0或k2=1。这种情况可以通过取代这个值把k2=PREC或k2=1-PREC来处理,PREC被当做1E-10。因此,出口边缘是包括该顶点的两个边缘之一。
C(t)最后接近于连接交点的折线Ch(t)。
图4.从u(t)的k=0迭代开始,跟踪网格上的参考纤维:3D元素ABC被投射成xoy平面上的abc,u(t)是ox轴
图5.跟踪网格上的参考纤维从u(t)的k = 1迭代开始
图6.从TA到TB更新TC
- 局部程函方程的求解器
完整的算法在[16,18]中有详细描述。由于在文献中有详细的记载,为了清楚起见,这里仅呈现网格中的锐角三角形的情况。有关局部求解器的详细信息和钝角
三角形的情况,读者应参考[16,18]。这里要解决的问题可以表示如下::知道网格元素的两个节点的行进时间,我们如何将这些信息传播到元素的第三个节点。考虑ABC是一个急性网格元素,如图6所示。局部求解器是一种算法,用于在铺放时间TA和TB的情况下更新顶点C处的行进时间TC。它使用一阶近似来局部模拟元件ABC内的纤维的铺放。角的顶点A,B,C分别为alpha;,beta;,gamma;。在网格元素ABC中纤维局部变直并且这段必须经过C(惠更斯原理)。这个条件是满足当且仅当(见图5):
- (TB-TA)/fle;AB:纤维可以在(TB-TA)的时间内以1/f的速度由A到B
- theta;le;beta;:纤维经过C之前的B
- theta; beta;le;Pi;/2:穿过C的正交线纤维在ABC内,这意味着C由A和B更新得来。
这些因素构成在算法1中的局部求解。请注意,使用“最小”是因为根据第5节中给出的快速匹配方法可以重复多次使用局部求解器进行C更新。因此TC的最小值必须被保存。
- 快速匹配法
在这个部分,快速匹配法被重新提起。这个方法是用来跟踪接口以1/f的速度来运动,确保它始终与自身正常。它旨在通过使用前一节的局部求解器跟踪每个元素内的运动来模拟参考纤维的完整铺放。该算法在每个节点x处计算接口已经通过的时刻T(x)。在计算所有节点通过的时刻之后,时刻T的接口位置是等值曲线T(x)= T。在算法的初始化步骤中,通过网格跟踪参考纤维之后,节点的网格被分为三组:冻结,近距离和远距离。冻结节点是元素节点的集合。冻结节点是参考纤维已经通过的节点的结合。近距离的节点是一组挨着冻结节点的节点。远距离节点是剩余的节点(见图7)。每个冻结节点的T(x)被初始化为与参考纤维时间f的距离。其他节点的T(x)被初始化为无穷大。最后,对于近距离节点集合中的每个节点C,并且对于每个网格元素ABC,使用上述局部求解器从TA和TB更新TC。FMM依赖于信息从较小的T铺放到较大的信息的原理。这被称为逆风方案。移动接口是在冻结点和近距离点之间的区域。在每个迭代中,让C成为近距离节点组的一员,这个近距离组必须包含最小的T值。移动这组近距离点并且将它添加到冻结点集合中。让M点与远距离点C点的临近。把M节点从远距离组移动到近距离组。使用局部求解器把ABM中每个元素从TM更新到TB和TA。当所有节点在冻结点集合中时算法必须终止。对于由n个节点组成的网格,FMM具有O(nlogn)的总操作数,以在整个网格中找到T(x)值。有关快速匹配法的更多详细信息,请参阅[16,18]。
图7.快速匹配法:冻结节点(黑点),近节点(白色方块)和远节点(白点)
- 方法的适用
在图8和图9所举例的两种情况下,快速匹配法并不能准确的产生预期的纤维网格,即使该解决方案存在于等距离轨迹中。考虑图8中的第一种情况,其中直线等距纤维将被定义在矩形域上。参考纤维是一个有界的段。该段在整个段中的铺放是由程序段中两个尾部的正交线所定义的。程序段外的区域由弧线圈所填满。即使FMM提供了一组等距轨迹,但最后的纤维网格也不是所预期的。最后见图10。
此问题的解决方案是模拟无限的参考纤维的铺放,而不是有限的参考纤维。然后如下修改2D局部求解器。
让A成为边界域上一个更新的节点。计算纤维在A内部域的纤维取向和A上纤维的正交平面。这个平面将覆盖表面划分为两个部分:一个带有平行纤维和一个带有圆形的弧线。为了模拟无限纤韦(为了消除圆弧),该算法在圆弧部分中查找A的所有邻近节点。在图11中,这些点是B和C。如图11所示,B的更新是由TB=TA d所赋予,其中d是C与纤维的局部扩展之间的距离
全文共6024字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[143049],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


