英语原文共 23 页,剩余内容已隐藏,支付完成后下载完整资料
5.4齿轮诊断
在第二章中描述了齿轮振动产生的基本原因,包括在正常情况下产生的振动和由于各种故障所产生的振动。需要指出的是,由于齿廓每次啮合的方式相同,所以齿轮的振动往往是确定的。由于有速度波动,图片中会出现随机性。但是第三章3.6.1节中的指令追踪程序可以用来抵消它,并且通常被用来作为时域同步平均技术的初级形式。要注意的是这实际上改变了时间轴的旋转角度,但是TSA这个词将会一直在这本书中被使用,直到机器具有名义上的恒速。随机载荷(如如岩石破碎机或风力涡轮机)也会导致随机性的产生,然后情况将会变得更加复杂。在负载随时间变化的情况下,但只有在变化相对缓慢的前提下,当负载在某一特定的指定范围(可能是由反复试验决定的最佳值),通常可以进行记录,然后只能在相同的负载条件下进行比较。不同负载范围的数据可以作为参考。以下主要讨论的情况是,可对微小速度变化做出补偿,并且负载的变化范围是有限的。速度和负载变化的情况将在5.4.5节中简要的介绍。
5.4.1基于时域同步平均技术
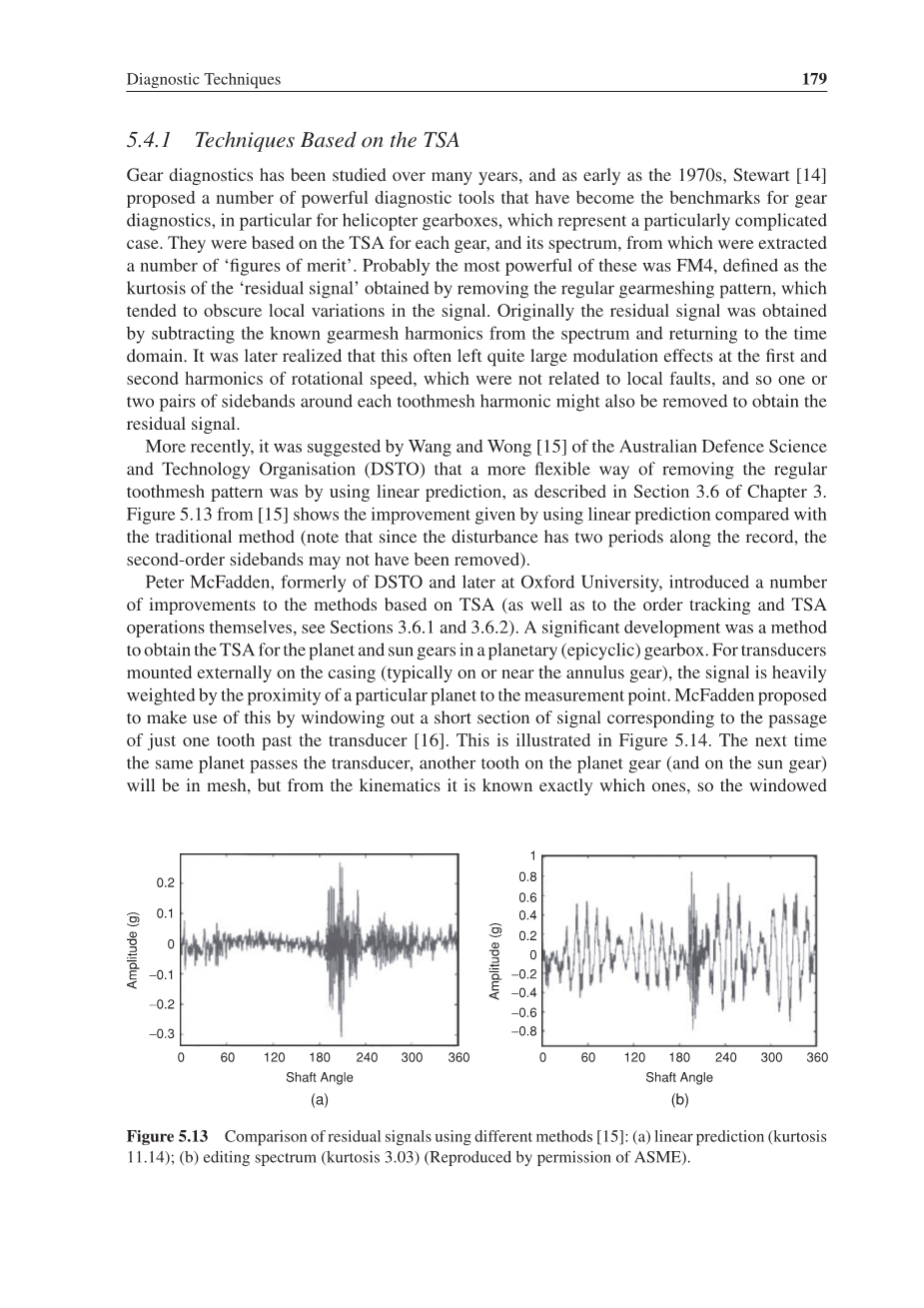
齿轮诊断学已经研究了很多年,早在20世纪70年代,斯图尔特(stewart)提出了一些强大的诊断工具,已成为齿轮诊断的基准,特别是为直升机齿轮箱诊断,这是一个特别复杂的案例。他们对每一个齿轮和及其频谱,通过时域同步平均技术从中提取一些有用的数据。可能其中最有用的数据是FM4,会使信号产生模糊的局部变化,它被定义为残余信号的峰度,是通过移除常规齿轮模式来获得的。最初,这参与信号是通过从光谱中减去已知齿轮啮合谐波然后回到时域中得到的。后来才意识到,这会对第一和第二谐波的转速造成很大幅度的影响,这与局部故障无关。所以也可能是齿轮啮合谐波的一对或两对边带被删除而得到残余信号。就在最近,澳大利亚国防科学与技术组织的Wang and Wong提出:利用线性预测技术是除去常规齿轮啮合模式更灵活的方式,这在第三章的3.6.1节中有介绍。图5.13显示出利用线性预测方法与传统的方法相比得到的改进(需要注意的是,根据记录可知由于扰动有两个时期,所以二阶边带可能不会被删除)。
麦克法登(Peter McFadden),早前是在澳大利亚国防科学与技术组织后来在牛津大学,基于时域同步平均技术介绍了一些改进方法(不仅关于指令追踪程序也关于时域同步平均技术的使用,在3.6.1和3.6.2节可看到)。一个重要的改进是得到一个行星(周转)轮系齿轮箱中行星轮和太阳轮的时域同步平均值的方法。对于安装在外壳上的传感器(通常是在环形齿轮上或者附近),信号主要是被附近的某一特定行星轮加到测量点上的。麦克法登(McFadden)提出可以在这信号中,通过窗口找出与一个轮齿通过了传感器时的通道相对应的一短段信号来。如图5.14所示。下一次行星轮通过传感器时,行星轮(和太阳轮)上的另一个轮齿将会啮合,从运动学角度来讲可以知道确切的是哪一个轮齿,因此每个轮齿和每个齿轮的信号都能被显示在不同的地方。当通过足够数量之后,行星轮和太阳轮上的轮齿不仅会碰到,而且会碰到几次,以至于会在窗口部分能平均显示出每一个轮齿的时域同步平均信号,然后把它们综合在一起就是整个齿轮的信号了。这是用于每一个行星轮和太阳轮(所有行星轮能够通过啮合信号得到每个轮齿的时域同步平均信号)。在原文中,麦克法登用一个矩形窗口对应一个轮齿啮合的时段,但在后来的文件中,他又推荐了一个轮齿啮合时段两倍总长度的汉宁窗口(他在书上称之为图基窗)。时域同步平均信号波形中几乎没有明显的差异,但是在后者的频谱中有相当大的改进,应该指出的是,对于行星齿轮箱中每一对啮合中的(单级)齿轮来说,其轮齿啮合频率(即轮齿啮合时间)是相同的。固定环齿轮(最常见的情况)与行星齿轮架是相同的,速度是环形齿轮上轮齿速度的几倍,因此它是行星齿轮架的谐波而不是太阳轮的。
图5.13 使用不同方法对残余信号进行的比较:(a)线性预测(峰度11.14);(b)编辑谱(峰度3.03)(经美国机械工程师协会许可转载)。
图5.14 据图显示当一个行星轮经过环形齿轮上某一个特殊的点时,会有一个特殊的轮齿与太阳轮接触以及另一个轮齿和环形齿轮接触(经Elsevier许可转载)。
另一个主要的贡献是希尔伯特利用转换技术,将时域同步平均信号(以齿轮啮合谐波为载体)调解显示为眼睛不可见的局部变化。图5.15显示了一个解调有裂纹齿轮的时域同步平均信号的典型例子,从信号开始被记录起齿轮实际上故障了103小时,在最后的故障之前齿轮的故障更为明显,在齿轮处于故障期间,只有使用信号分析技术,否则没有任何的进展。在这种情况下对齿轮啮合频率第二次的谐波进行解调是因为在加速度方面,它要远远强于第一次的谐波,从而能得到一个更好的信号噪声比。
图5.15 有裂纹齿轮的轮齿啮合频率的第二谐波的解调:(a)时域同步平均后的时间信号;(b)振幅调制信号;(c)相位调制信号(经美国机械工程师许可后转载)
需要指出的是,这项技术受到调制信号带宽的限制,就好像最大的带宽能被解调为对应的加减一半的轮齿啮合频率一样,独立的谐波也能被解调。这在下面5.4.2节中有介绍,在这一节中加速度信号和传输误差信号都进行了解调,为了能看到这两种信号的幅度和相位调制的相互关系。在这些情况中如果故障引发非常高频率的共鸣,那么可能是由于轮齿啮合频率信号解调的条件没有达到而造成的。有一个关于风力涡轮机齿轮箱类似的例子在5.4.5节中有提到。这个类似的例子表明了同步平均的方法并不能在所有的情况下都适用,还取决于不同频率范围内不同故障的不同表现,会在后面的5.4.5中介绍到。
5.4.2 传动误差作为一种诊断工具
齿轮诊断在一定程度上受从开始点到测量点这段的修正信号的影响,因此在轮齿啮合点进行测量是有意义的。这种可能性是有传输误差的测量造成的,如果精确的轴编码器能够被安装在装有齿轮的轴上,那么这是可能的,特别是自由(非驱动)的结束,这是在任何情况下通常最容易达到的。如果轴上没有驱动力矩将齿轮连接到编码器上,那么轴就会跟随着齿轮的转动准确地振动到一个非常高的频率。
就像在2.2.2节中介绍的一样,传动误差表示从动齿轮的角运动之间的区别,如果传动过程能够完美进行,那么就会以恒定的速度进行也会以恒定的速度停止。虽然通常用一个齿轮或另一个齿轮的角度偏差来衡量,它只对应这对齿轮沿着两齿轮节圆公切线方向的线性偏差,因此必须按比例缩小传动比,使两齿轮有相同的初始条件。因此可以通过测量每个齿轮的扭转振动,再按传动比缩小,使其等效于其他的线性运动,然后再减去其他不需要测量的齿轮的扭转振动来得到要测量的结果。这通常被理解为输出减去输入,也可以表示为任一齿轮的转动或者节圆上的线性运动。缩小纯粹是对波动幅度而言,因为齿轮的时间轴是独立的。
图5.16 带有模拟齿根裂纹的齿轮的传动误差:(a)齿轮1的相位;(b)齿轮2的相位;(c)相减后的传动误差;(d)模拟裂纹
图5.16显示了在一个齿轮箱中因为两根轴的扭转振动而导致的传动误差的产生,该齿轮箱中有一个具有模拟齿根裂纹的齿轮。因为传动比为1:1(每个齿轮上有32个齿),所以扭转振动信号在相减之前不需要进行缩放。扭转振动可以通过用图3.30(b)中的程序说明来处理每根轴上的轴编码器获得的相位解调信号来测得。需要注意的是,每个齿轮的相位呈现出一些随机的速度变化(相位曲线的局部斜率),但是传动误差不一样,它具有非常有规律的周期性的转速。还注意到传动误差的规模与原来的扭转振动信号相比也有所不同。速度是3赫兹表示在一秒内有三次转动。
还需要注意的是,轮齿啮合信号非常的清楚(每个周期有32个时段),并且局部偏差也很明显(第一个大概0.11秒)。在这种情况下,传动误差信号中的局部故障是明显的(但并不是在所有的速度和载荷下都是这种情况),但是被三个阶段的信号处理大大地改善了,如图5.17中所示。
图5.17 由图5.15(c)得到的故障指示增强:(a)通过移除轮齿啮合谐波所剩余的;(b)通过高通过滤移除啮合频率一半的低频趋势;(c)(a) (b)后得到的结果。
这种测量齿轮传动误差的方法首次被发表在(19)上,作为P.J.思威尼博士论文的一部分。该编码器信号的相位解调(和结果的频率分析)是使用了在3.3.2.2节中的变焦处理器方法得到的,使用的是2035型BRuml;UEL和KJaelig;R分析仪。在图5.18中,其结果与思威尼发明的脉冲计时方法相比,使用一个100MHz的时钟对编码器脉冲的时间间隔进行计时。这种方法基于一个很简单的原理,编码器脉冲间的时间间隔给了相位角常数增量时间一种测量标准(因此可以作为一种指令追踪方法用来进行角度测量,在3.6.1节中有进行描述)。时间间隔的倒数可以根据瞬时角速度标准化得到频率调制,并且具有这样的优点:一个循环内的样本数目是固定的,以至不需要进行指令追踪。这种方法对于测量往复式机械的扭转振动也是很有用的,因此将会在5.6.2.2中再次进行介绍。在思威尼进行论文工作的时候使用这样的高频时钟是非常困难的,并且相位调制更为实用,但是商业数据采集系统现在可以使用一个80MHz的时钟,这使得脉冲计时技术更为可行。
图5.18 齿轮传动误差的测量是通过相位和频率调制的到的,而这又是利用放大解调和脉冲计时从每个齿轮上的转轴编码器信号中得到:左,时间信号;右,频谱(经圣人出版物许可转载)
值得注意的是这两种方法所得的结果几乎是相同的。测量结果的精确性使人印象深刻,因为它主要是根据采样的精确度和时钟的计时,并不受模拟仪表精度的影响(如以前用于齿轮传动误差测量的相位计一样)。海德汉ROD260型号编码器用在这里,具有很高的精度,只会出现三到五弧秒的误差。然而从结果可以看出来,这些小误差都集中出现在旋转低谐波上(可能主要是由于刻光盘的微小偏心距造成的),误差也比对应轮齿啮合频率高次谐波要更小一点。在这种特殊情况下,测得的传动误差低谐波和轮齿啮合频率值大约是五十弧秒,每一弧秒等同于在节圆上进行0.025微米的线性运动。
有记录误差的轴编码器是很昂贵的,因此都和兰达尔在研究测量和校正编码器误差的方法,特别是便宜的编码器。在(20)中有解释这种方法,先进行两次测量,然后将两者之间的编码器进行交换,通过对不同测量结果的比较得到两编码器的共同误差是可行的,两次结果的平均就是真实结果的最佳估计。这个简单的方法适用于传动比为1:1的齿轮,因此得出的结果与两次测量结果和给定的误差值大致相同。图5.19显示在相同的实验台上的直齿和斜齿圆柱齿轮的一个典型结果(齿数分别为32和29齿)。它确保了编码器的对齐方式与两组测量的起始位置是相同的。两次的实验对比显示出了,传动误差要比轴编码器误差要大十倍。
可以看出,斜齿圆柱齿轮的传动误差要比直齿圆柱齿轮小得多(尽管由于齿距误差导致的低频分量相同),编码器的误差在两次测量中实际上是相同的,从而验证了该方法是有效的。图5.20显示的结果对这进行了进一步的验证,在一对传动比不是1:1的直齿圆柱齿轮进行测量(32:49)。在这种情况下,编码器在两次测量中的旋转速度不同,然后互相进行交换,对测量结果进行对比得到两个不同的编码器共有误差,一个是每个齿轮的旋转周期。然而,可以通过时域平均提取出一个齿轮周期,如图5.20显示。需要注意的是传动误差的基本周期对应着32齿齿轮的49次转动(图上仅显示出两次)。通过时域平均提取出的一个32齿齿轮的编码器误差与图5.19显示的非常相似,即使是通过平均处理之后。它的频谱显示,误差集中显示在旋转速度的低谐波中,并不是远远大于昂贵编码器的误差。
图5.19 传动比为1:1的齿轮的传动误差和编码器共有误差的测量:左边,直齿圆柱齿轮(32齿);右边,斜齿圆柱齿轮(29齿)(经圣人出版物有限公司许可转载)。
图5.20 传动比为32:49的齿轮的编码器误差测量:左边,交换编码器后的32齿齿轮的两次转动的传动误差测量;右边,通过时域平均提取的32齿齿轮的时间记录和公有的编码器误差谱(经圣人出版物有限公司许可转载)。
使用低成本的编码器(海德汉426型)测量出来的误差是足够小的以至于都(Du)觉得没有必要在他的论文中进行介绍,这在(21)中有记载。
将同一时间得到的传动误差解调与加速度信号测量结果进行比较是很有趣的。图5.21显示出与图5.16中相同齿轮的传动误差结果,可以看出,解调的振幅显示出的故障很清楚,而相位却没能清楚的显示。
图5.22显示了对加速度信号解调的结果(包括了对传动误差振幅解调来作比较)。很明显,加速度信号是包含更多有关裂纹信息的调制信号。这在一定程度上可以根据实际被解释,传动误差的幅度直接给出了转矩的变化,这也许可以解释频率和相位调制的变化,但需要注意的是它还取决于啮合时力和测量点加速度之间的函数关系。
图5.21 一个具有模拟齿根裂纹的齿轮的传动误差信号的解调结果:(a)振幅解调;(b)转速信号;(c)相位解调;(d)传动误差信号。
图5.22 对传动误差和加速度信号解调结果的比较:(a)传动误差振幅解调;(b)转速信号;(c)加速度振幅解调;(d)加速度相位解调。
图5.23 传递函数改变振幅和相位调制的分布的描述
图5.23显示了一个简单的例子,一个简单的调幅可以通过一个函数转化为振幅和相位调制的混合。如图3.29所示,正是基于这样的事实,振幅和相位/频率调制之间的主要区别是在边带的任一侧上的载波的相位关系。传递函数的相位变化(图5.23没有显示出)将会造成幅度和相位调制的更多变化。
因此,使用传动误差作为一个诊断参数的一个可能的优点是将会从振幅和相位调制的不同推断出更多结果。
在结束这个话题之前,将会展示如何围绕从图5.21和5.22
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[147111],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


