基于时间序列分析的短期负荷预测:一个案例研究外文翻译资料

英语原文共 5 页，剩余内容已隐藏，支付完成后下载完整资料

基于时间序列分析的短期负荷预测:一个案例研究

1. N.Dodamani,V.J.Shetty,R.B.Magadum

Assistant.Professor,Gogte Institute of Technology,Belagavi,Karnataka

摘要

短期负荷预测在日常发电、高效的电力系统规划、机组维护、确定机组投入以及保障电力系统安全运行等方面起着至关重要的作用。短期负荷预测的方法有很多，但时间序列方法是最可行的，可以提供更合理、准确的预测。本文讨论了泰米尔纳德邦(印度)负荷数据短期负荷预测的时间序列分析的自回归方法。时间序列自回归法提前4～6小时给出了较好的预测结果。

关键词：自回归(AR)模型，负载数据，均方根平方误差(RMSE)，短期负荷预测，时间序列分析

1.介绍

负荷预测是电力系统管理的重要内容，是电力系统能否成功运行的重要基础因素[2]。为了有效和最佳地运行电力系统，必须精确地预测未来的负荷数据。近年来，短期负荷预测越来越受到重视，主要有两个原因:一是电力系统的去监管化，并且事实上没有两个实用程序是相同的，这就需要详细分析影响负载需求的不同地理、气象、负载类型和社会因素[3]。另一方面，如果系统负荷预测偏低，可能会影响系统的可靠性和安全性，从而导致电力中断。

负荷预测基本上可以分为两类:短期负荷预测和长期负荷预测。长期负荷预测通常用于处理较长的预测周期，其预测结果可用于电站的长期维护、经济运行和扩容[2]。然而，短期负荷预测预测的是一个小时到几个小时的负荷信息。对单个电站，电站的管理和控制等许多功能都需要提供实时电价对用户和规划负荷处理能力[4]。

在目前的电力情况下，由于客户数量的增加，负荷需求也在急剧增加。不同行业的负荷需求受不同因素的影响，准确的预测成为一项繁琐的工作。因此，为了克服这些问题，短期负荷预测被用来估计负荷流和采取适当的决策，可以防止系统超载。及时执行这类决策可使电力系统可靠、安全、健康地运行，将设备故障、限电和停电降至最低。

为了获得更高的系统预测精度，人们开发了不同的方法和技术，如时间序列分析、metro数值预测和混合模糊神经方法[5-6]。

其中，时间序列分析是研究的主要领域，其研究成果丰富，对各种背景下的数据有专门制定的方法[2]。

通过文献调查发现，在众多工具中，时间序列模型是一种强大而有效的工具。本文将电力系统的负荷模式应用于电力系统的负荷预测。

随着农业成为泰米尔纳德邦最大的电力消耗大户，泰米尔纳德邦成为首批实施大规模农村电气化计划的邦之一。目前，泰米尔纳德邦电力委员会(TNEB)是一家国有企业，是主要的能源供应商和分销商。泰米尔纳德邦的网格地图如图l所示。泰米尔纳德邦所有可用资源的总装机容量列于表1[7]。

图1印度泰米尔纳德邦网格地图[8]

表1印度泰米尔纳德邦的装机容量

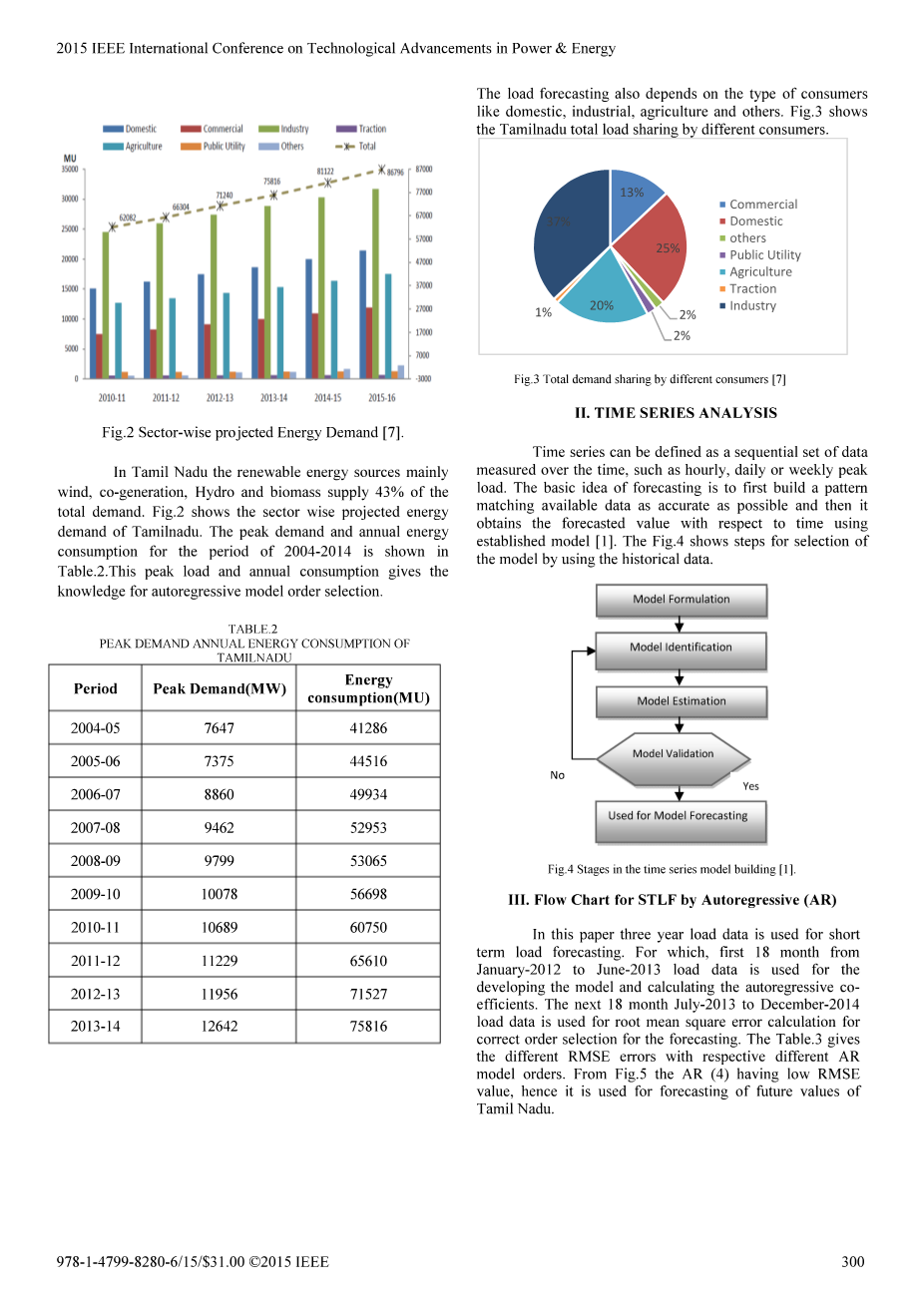
在泰米尔纳德邦，可再生能源主要是风能、热电联产、水能和生物质能，占总需求的43%。图2显示了泰米尔纳德邦的区域能源需求预测。2004-2014年的需求峰值和年能耗如表2所示。这个峰值负荷和年消耗为自回归模型的顺序选择提供了依据。

图2分段预测的能源需求[7]

表2泰米尔纳德邦年度能源消耗峰值

负荷预测还取决于消费者的类型，如家庭、工业、农业和其他。图3为不同用户共享泰米尔纳德邦总负载情况。

图3不同消费者的总需求分担情况

2.时间序列分析

时间序列可以定义为一组按时间度量的连续数据，例如每小时、每天或每周的峰值负载。预测的基本思想是先建立尽可能精确的可用数据的模式匹配，然后利用所建立的模型得到关于时间的预测值。图A显示了使用历史数据选择模型的步骤[1]。

图4时间序列模型构建的阶

3.自回归(AR)短期负荷预测流程图

本文采用三年负荷数据进行短期负荷预测。其中，2012年1月至20l3年6月的前18个月负荷数据用于模型的建立和自回归系数的计算。利用2013年7月至2014年12月的18个月负荷数据进行均方根误差计算，为预测提供正确的序选择。表3给出了不同AR模型阶数下的不同均方根误差。从图5可以看出，AR(4)的均方根误差值较低，因此可以用来预测泰米尔纳德邦的未来值。

.

图5时序分析负荷预测流程图

4.案例研究和仿真结果

泰米尔纳德邦可用负荷数据用于电力系统运行研究的短期负荷预测。从2012年1月到2014年12月，每分钟的时间段都有负载数据。最后以一小时为间隔进行案例研究。图6、图7、图8分别为2012年、2013年和2014年的负荷变化，x轴为时间(Hrs)，y轴为负荷需求(MW)。

图6 2012年1-12月负荷数据

图7 2013年1-12月负荷数据

图8 2014年1-12月负荷数据

利用三年负荷数据进行自回归参数的预测分析和RMSE计算，选择合适的序次。利用Microsoft visual basic开发了AR高效分离模块的计算。通过与以往软件结果的对比，如表3所示，验证了该方法的有效性。

表3微软VB.6中AR与已开发模块与以往软件效率对比

在开发的模块中增加了进一步的RMSE计算和预测功能。从图6可以看出，AR(4)的RMSE值最小。因此，它被用于负荷预测。

表4不同时间范围和不同AR模型阶次的RMSE值比较

利用AR(4)工具，考虑样本负荷数据进行样本预测，如图9所示。时间序列分析AR模型的预测结果较好，如表5所示。

图9不同阶自回归模型不同时间域的RMSE对比表

您可能感兴趣的文章

• 无线传感器网络：环境监测外文翻译资料
• 机器人视觉中的卡尔曼滤波研究进展外文翻译资料
• 混合动力汽车健康意识充电管理现状外文翻译资料
• 基于自适应加权的多目标PID控制器算法应用于蒸汽温度控制中锅炉外文翻译资料
• 机器人视觉的卡尔曼滤波器：一项调查外文翻译资料
• 测量研究系统的跨学科性：检测出版物类别和引用类别之间的区别外文翻译资料
• 深度图像:放大图像识别外文翻译资料
• 一个关于蓝牙、超宽带、ZigBee和Wi-Fi无线协议的比较研究外文翻译资料
• 使用双无线电节点实现集群无线Mesh网络的服务质量外文翻译资料
• 使用ZigBee设备和传感器网络的高效智能路灯远程控制系统外文翻译资料