英语原文共 14 页，剩余内容已隐藏，支付完成后下载完整资料

采用基于模型的增强自适应滤波方法控制调制振动

Byeongil Kim,Gregory N.Washington,Rajendra Singh

（美国俄亥俄州州立大学机械工程系智能汽车概念中心，西19大街201号）

摘要

传统的自适应滤波算法，通常局限于单个或多个正弦信号的控制，不适用于控制调制振动，特别是在存在丰富的侧带结构的情况下。针对这一不足，提出了一种新的控制算法，在自适应滤波系统中引入模型预测滑模控制的反馈环。首先对几种调幅和调频情况进行了计算研究，并从估计误差、时域和频域性能、参考信号的稳定性和不确定性等方面对常规方法和提出的方法进行了比较评价。为了实验验证所提出的算法，我们构造了一个具有纵向振动的主动杆。总体而言，所提出的自适应算法在主频率和边频带上都有较好的约简效果;此外，在宽带的基础上发现了良好的衰减。

1.介绍

通常在许多机械元件的振动声频谱中观察到边带结构旋转系统，例如齿轮，轴承，风扇和电动机[1-5]。尽管经常使用调制的频谱内容开发用于故障检测和预防性维护的算法，并排除实际的噪声和振动（或声音质量）问题，该问题的几个方面仍未得到很好的理解。例如调幅（AM）或调频（FM）理论没有完全描述测得的特征，尽管这些概念是有助于理解频率的存在[6]。另外，尝试主动抑制振幅或频率调制信号已经部分成功[7-9]。

尤其是，旋翼航空器机舱噪声继续构成挑战，因为变速箱产生了大量结构声被传送到机舱[10–14]。频谱内容通常在齿轮啮合频率及其侧面方面很丰富乐队[1-2、5、10]。图1示出了单个齿轮对的典型壳体加速度谱。有几位研究人员建议用于旋翼飞机的主动噪声或振动控制方法。Millott等。[11]提出了一个系统仅在几种操作条件下检查惯性执行器和第一齿轮啮合频率下的噪声降低。Gembler等。[12]，Maier等。[13]，和霍夫曼等。[14]开发了改进的主动支撑设计，发现基本齿轮啮合频率下的振动幅度大大降低，但更高的齿轮啮合在控制之后，谐波和边带保持不变，甚至放大。

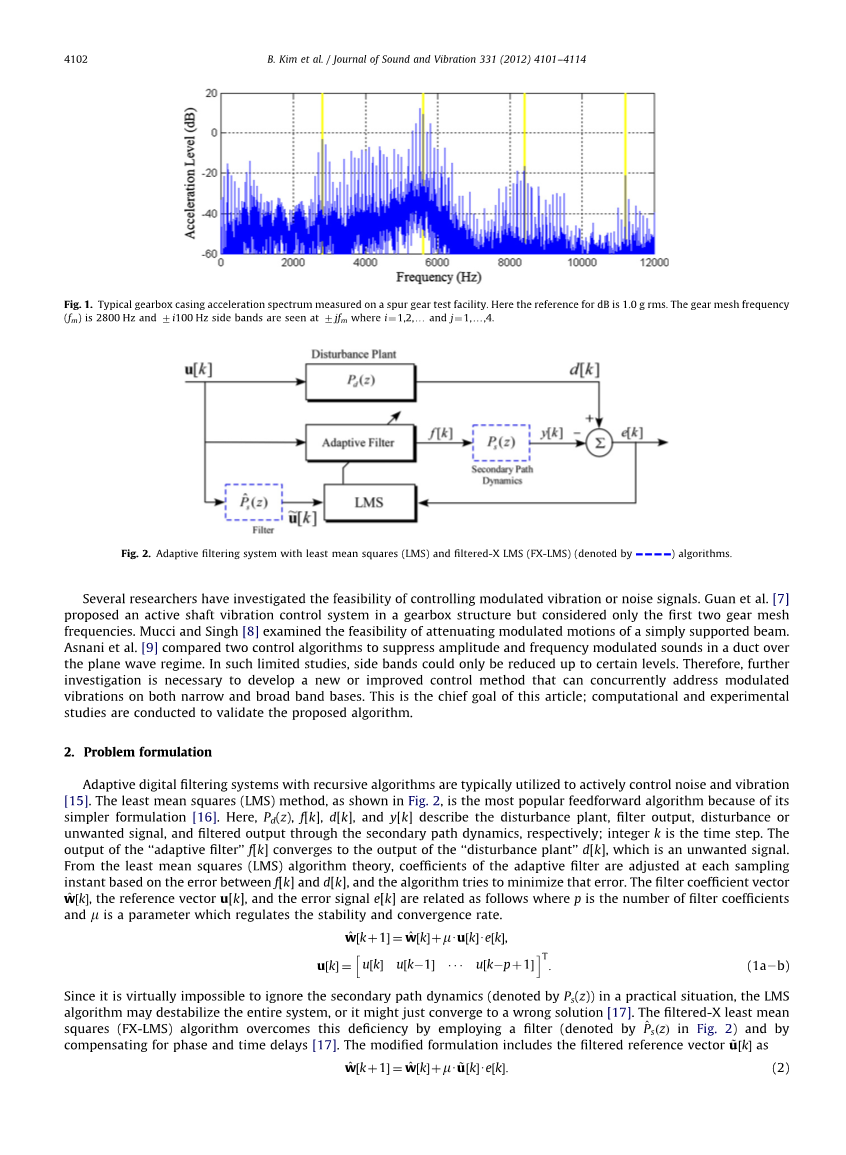
图1.1 .在正齿轮测试设备上测得的典型变速箱外壳加速度频谱。此处，dB的参考值为1.0 g rms。齿轮啮合频率（fm）为2800 Hz，在7jfm处看到7i100 Hz的边带，其中ifrac14;1,2，y和jfrac14;1，y，4。

图1.2 具有最小均方（LMS）和已过滤X LMS（FX-LMS）算法（由表示）的自适应过滤系统。

一些研究人员已经研究了控制调制振动或噪声信号的可行性。关等。[7]提出了一个主动轴振动控制系统的齿轮箱结构，但只考虑了前两个齿轮啮合频率。Mucci和Singh[8]研究了简支梁衰减调制运动的可行性。阿斯纳尼也等。[9]比较了两种控制算法在平面波状态下抑制管道内振幅和调频声音的效果。在这些有限的研究中，侧链只能减少到一定的水平。因此，有必要进一步研究开发一种新的或改进的控制方法，可以同时处理窄频和宽带基频的调制振动。这是本文的主要目标;通过计算和实验验证了该算法的有效性。

2.问题表述

具有递归算法的自适应数字滤波系统通常被用来主动控制噪声和振动。最小均方法(LMS)，如图所示。2、是目前最流行的前馈算法，因为它的公式比较简单[16]。这里，P(z)， f[k]， d[k]， y[k]分别描述了干扰植物、滤波输出、干扰或不需要的信号，以及通过二次路径动态滤波后的输出;d整数k是时间步长。“自适应滤波器”f[k]的输出收敛于“干扰厂”d[k]的输出，是一个不需要的信号。从最小均方(LMS)算法理论出发，根据f[k]和d[k]之间的误差，在每个采样时刻调整自适应滤波器的系数，使误差最小化。滤波器系数矢量wfrac12;k，参考矢量u [k]和误差信号e [k]如下相关，其中p是滤波器系数的数量。m是调节稳定性和收敛速度的参数。

（2.1）

（2.2）

由于在实际情况下实际上不可能忽略次级路径动力学（用Ps（z）表示），因此LMS该算法可能会破坏整个系统的稳定性，或者可能会收敛到错误的解决方案[17]。滤波X最小均方（FX-LMS）算法通过使用滤波器（在图2中用P ^seth;zTHORN;表示）和通过补偿相位和时间延迟[17]。修改后的公式包括过滤后的参考向量u〜frac12;k作为

（2.3）

表2.1 仿真研究总结及典型减振效果

表2.2 实验研究和典型减振的总结

传统的LMS算法至少有两种控制多光谱内容的方法。首先，使用一个多通道LMS方案，该方案包含与处理[18]的光谱内容数量相同的LMS块并行数量。其次，使用大量的滤波系数可以改善跟踪[19]。然而，这样的解决方案(计算量很大)在实际应用中可能无法充分处理许多复杂信号，包括调制干扰。Mucci和Singh[8]使用了FX-LMS，以最大限度地减少在一个位置的梁振动加速度计被放置在感觉误差。然而，一些光谱成分或非预期的调制(如实验系统非线性引起的调制)是无法控制的。最显著的衰减出现在载频处，而边带的残余误差与载频处相同或更大。阿斯纳尼也等。[9]在抵消模式下利用窄带自适应噪声均衡器(ANE)[20-22]，克服了部分不足;结果表明，该方法能完全消除载频和侧频带，取得了显著的效果。此外，ANE允许对单个频率分量的误差光谱进行整形，因此可以保留一些残留的噪声，尽管主要的边频带大大减少。然而，ANE需要对载流子频率和边频带的先验知识。

本文的具体目标包括:(1)开发一种新的控制算法，将基于模型的控制方法与非线性控制方法相结合，以增强传统的LMS算法，同时保留其固有的优势;(2)对表1中提出的AM和FM信号(以及两者的乘积)和高斯噪声的算法进行比较评价;(3)构建主动支杆，分别使用两种算法进行实验研究，测量多个调制振动信号的振动残差，如表2所示。本文还讨论了混叠参考信号或干扰模型的稳定性问题及其影响。

3.开发新的控制算法

3.1 概念上的注意事项

提出的算法如图3所示。一条水平线(虚线)区分了动态系统和控制系统。动态系统中，扰动量为P(z)，输入量为u[k]，输出量为d[k]，为不需要的信号。d其余部分为整个控制系统。将LMS算法与基于模型的非线性控制方案相结合。其中，n[k]为传感器噪声，q[k]为意外扰动，系统模型或信号的不确定性采用时变P(z)进行量化。s与传统自适应滤波的主要区别在于反馈回路的位置。LMS算法仍然试图使自适应滤波器的输出收敛于扰动厂的输出，只是为了更好地跟踪误差再次由反馈回路控制。模型预测滑模控制(MPSMC)方法在被辨识出来之后，可以根据P(z)来设计，虽然会得到一个非常粗略的模型。d反馈回路的控制输入c[k]，如第3节所示。2，用来创建一个修改后的滤波器输出m[k];定义如下:

（3.1）

表3.1 .提出了模型预测滑模-最小均方(MPSM-LMS)控制算法

然后，将m [k]用作Ps（z）的输入。注意，如图2所示，未使用滤波后的参考u〜frac12;k，因为可以由反馈回路管理源自Ps（z）的延迟，而无需u〜frac12;k。在此，定义跟踪误差e [k]

如下。

（3.2）

下面将讨论添加反馈循环的潜在优势。

跟踪性能:e[k]与f[k]之间的传递函数G_ef(z)决定了跟踪性能。

（3.3）

当|G_ef(z)|→0时，我们期望在较宽的频率范围内具有良好的跟踪性能。ef因此，任何由LMS引起的失调都可以通过调节反馈回路中的控制器P_l(z)来解决。

拒绝扰动:当自适应控制系统受到扰动q[k]时，反馈回路可以通过最小化e[k]对q[k]的灵敏度来实现。假设其他输入为零，误差传递函数E(z)/Q(z)和E(z)/F(z)可以计算出来。

（3.4）

（3.5）

假设|P_s(z)P_l(z)|gt;gt;1,扰动的影响可能是抑制自|EQ(z)/Q(z)|lt;lt;1,相反，9E(z)/ F(z)9-91/P(z)9，因此性能不应受到P(z)变化的影响。Fls

低灵敏度时变路径动态:定义传递函数估计的实际路径动态P (z) ^eth;zTHORN;,和估计误差ss

（3.6）

G(z)的变化来自于Eqs。ef(5)(8)。

（3.7）

从方程式。(5)和(9)灵敏度Phi;(z)定义如下:

（3.8)

(3.9)

当9 peth;zTHORN;p ^eth;zTHORN;9c1 9 feth;zTHORN;9{1,因此对DG DP (z)的影响(z)是减少与前馈只有系统进行比较。lssef因此，利用反馈系统可以实现更精确的控制。

传感器噪声灵敏度低:传感器噪声灵敏度与传递函数G(z)有关，定义为:en

(3.10)

在P(z)的帮助下使9G(z)9最小，可以减小传感器噪声对系统性能的影响。enl

提出的概念考虑采用连续的误差减少方法。LMS算法和反馈控制器在每个时刻时刻依次应用[k]。两者本质上可以相互独立设计。最后，反馈控制系统的使用理论上应该能够降低外界扰动、传感器噪声和系统参数变化的敏感性。

3.2 模型预测滑模控制(MPSMC)

滑模控制(SMC)是一类非线性控制技术。不连续的控制输入驱动目标系统在一个不连续的滑动面两侧之间的状态，最终达到滑动模态，这定义了期望的系统特性。由于这种类型的控制器通常具有更强的鲁棒性，并且对原始植物动力学和其他意外情况不敏感，因此它

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[236865]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

您可能感兴趣的文章

• 连续气流作用下液滴变形到破袋和破袋的转变外文翻译资料
• 有机发光二极管:节能照明技术综述外文翻译资料
• 船用螺旋桨的集成曲面 造型和加工方法.外文翻译资料
• 混合功能化石墨纳米片/三聚磷酸盐在环氧涂层碳钢中的电化学反应和抗腐蚀反应外文翻译资料
• 双柱塞式液压系统的详细描述外文翻译资料
• 以可再生能源作为清洁动力的船舶性能外文翻译资料
• 船舶氮化物和硫化物排放的控制分析外文翻译资料
• 政策的角度第三方船舶管理:希腊的角度来看外文翻译资料
• 基于GW4D20柴油机的气缸盖温度场的实验和数值分析外文翻译资料
• 船舶电力系统的过去、现在和未来挑战外文翻译资料