
英语原文共 22 页,剩余内容已隐藏,支付完成后下载完整资料
非线性吸振器结构的复动力学
摘要:本文研究了非线性吸振器结构的非线性行为。该非线性吸振器结构是线性的,并且受谐波激励,模拟为一个单自由度受迫振荡器。非线性吸振器被建模为一个由质量、非线性弹簧和线性阻尼器组成的振荡器。基于数值解提出了一种全局分岔图,揭示了非线性吸振器质量和刚度变化时周期运动和无序运动的共存性。通过相位轨迹,功率谱和庞加莱图在数字上识别混乱。利用周期稳态响应的谐波平衡法预测了幅频响应曲线。 分析了它们的稳定性。 确定Hopf分叉和鞍节点分叉。 研究表明,非线性吸振器可能会产生动态复杂性。
关键词:非线性吸振器,全局分岔,紊乱,谐波平衡法,稳定性
- 简介
在一些开创性的工作[1,2]中,非线性吸振器是减少机械和结构的被动振动的有效装置。与早期的减少自由振动相比人们更加关注抑制结构在外激励作用下的受迫振动。这些结构被建模为单自由度振荡器[5–19],二自由度线性振荡器[20–23],线性弦[24,25],线性梁[26,27], 和单自由度非线性振荡器[28]。非线性吸振器的最简单模型是基本的非线性振荡器,它由较小的质量,立方刚度和线性阻尼器组成[5,7,8,10,15,16,20,22–28]。大多数可用的研究集中在周期性稳态响应[5,8–10,12,13,15–20,22–28]。除了实验工作[5,7,16,23]和数值模拟[5,6,9–14,17–19,21–23,26,28]之外,近似分析方法是通过屈服幅频响应曲线并检查其稳定性来预测稳态响应的有力方法[5–13,15–21,24–28]。最常用的方法是络合平均法[5,6,9,11–13,16,17,19–21,26–28]。在该方法的应用中,所得到的非线性代数方程很难数值求解。这个困难可以通过弧长延拓技术来克服[26-28]。谐波平衡法也被用来分析周期稳态响应[8]。此外,本文还提出了一种多尺度/谐波混合平衡算法,并将其应用于二自由度非线性系统[15]和包含内共振和非共振的弹性弦[24]中。除了周期运动外,还研究了弱准周期响应[7,8,10,21,25]、具有鞍结分叉的强调制响应[9,11,12]和混乱状态[6,8,14]。
非线性既可以定性地改变系统的动力学特性,也可以定量地改变系统的动力学特性。具体来说,非线性可能导致新的复杂动力学,如混沌,混沌运动的可能性最初在文献[8]中被揭示,混沌被李雅普诺夫指数[6]和梅尔尼科夫的方法[14]检验。众所周知,混沌路径对于理解系统的非线性行为是至关重要的。然而,对于一个由结构和非线性吸振器组成的系统,混沌的路径还没有得到研究。为了解决这方面缺乏研究的问题,本工作通过检查庞加莱图中的全局分叉,探讨了非线性吸振器的两个关键设计参数,即质量和非线性刚度,从而探索了混沌的路径。以全面了解非线性吸振器所产生的动态复杂性,导出了周期稳态响应曲线的幅频响应曲线借助伪弧长延拓技术,从谐波平衡的角度出发,研究了不同非线性吸振器质量和刚度的情况。分析了响应的稳定性,重点分析了Hopf分岔和鞍节点分岔的位置。
原稿的编排如下。第二节介绍了具有非线性吸振器结构的基本模型。在第三节中数值计算了全局分岔图,并对混沌进行了数值识别。在第四节中用谐波平衡法确定幅频响应曲线,并用直接数值积分法进行支持。第五节以结束语结束手稿。
- 具有非线性吸振器的线性单自由度系统
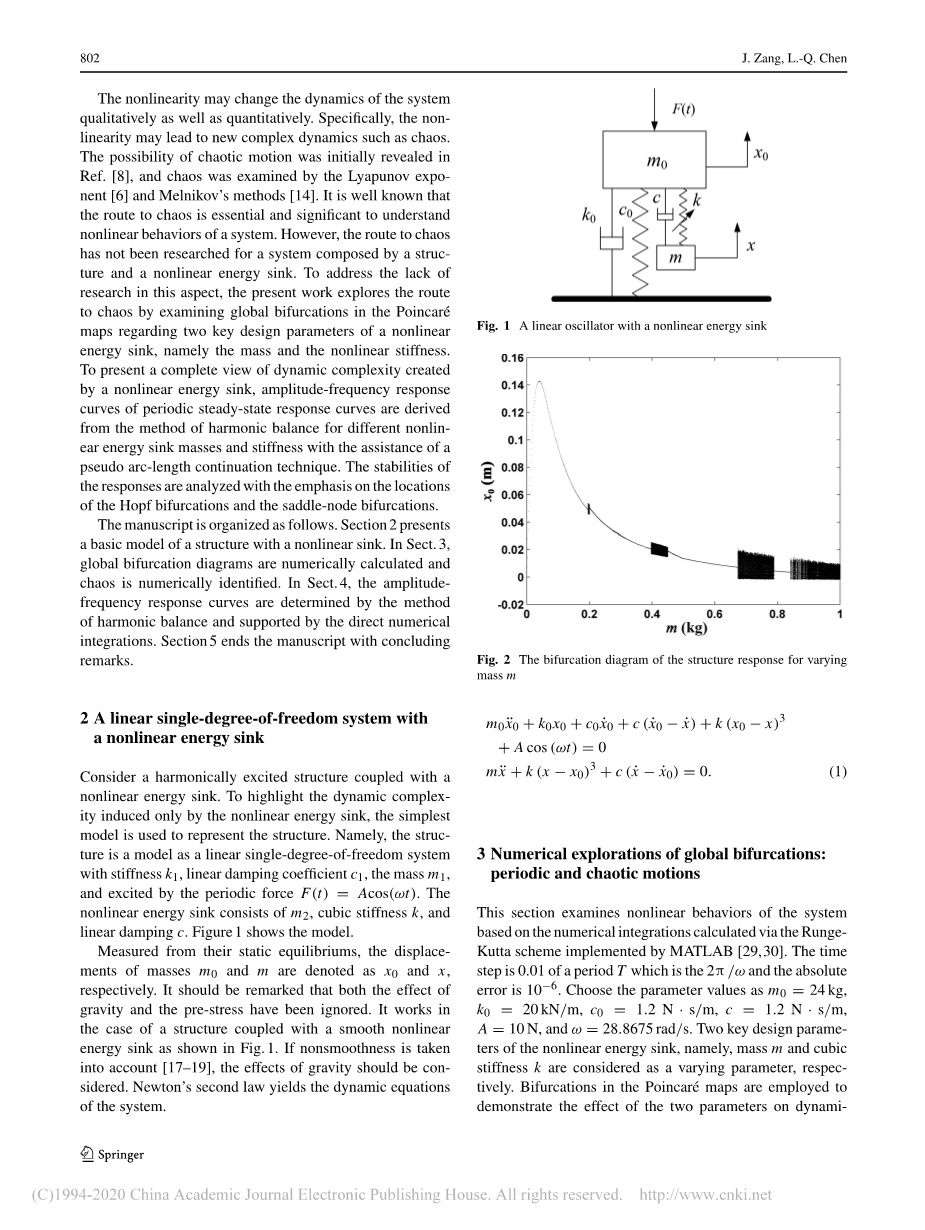
考虑一个与非线性吸振器的谐波激发结构。为了突出仅由非线性吸振器引起的动态复杂性,使用最简单的模型来表示结构。即该结构是具有刚度k1,线性阻尼系数c1,质量m1并由周期力F(t)= Acos(omega;t)激励的线性单自由度系统模型。非线性吸振器由m2,立方刚度k和线性阻尼c组成。 图1显示了该模型。
从它们的静态平衡测量,质量m0和m的位移分别表示为x0和x。值得注意的是,重力和预应力的影响都被忽略了。如图1所示,它适用于与平滑非线性吸振器的结构。如果考虑到非光滑性[17-19],则应考虑重力的影响。根据牛顿第二定律得到系统的动力学方程。
(1)
(非线性动力吸振器
- 全局分岔的数值研究:周期和混沌运动
本节基于通过MATLAB [29,30]实现的Runge Kutta方案计算出的数值积分,研究了系统的非线性行为。 tim步长是周期T的0.01,即T=2pi;/omega;,绝对误差为。 选择参数值,即m0=24kg,
K0=20KN/m ,c0=1.2Nbull;s/m,c=1.2Nbull;s/m,A=10N,omega;=28.8675rad/s。非线性吸振器的两个关键设计参数,即质量m和立方刚度k分别被视为一个变化参数。 用庞加莱图中的分叉来证明这两个参数对动力学行为的影响。 庞加莱图中的位移分量被聚集。 计算庞加莱图中的前4800个周期,只有最后200个周期被绘制在分岔图中,以消除瞬态响应。
(不同质量m的吸振器响应分岔图)
( 不同质量m的结构响应分岔图)
(m=0.2496kg的结构周期性振动.a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
(m=0.2496kg的动力吸振器的混沌运动a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
(m的结构的第1周期运动= 0.3384kg.a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
(m的结构的第2周期运动= 0.3384kg.a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
(m=0.72kg的结构的混沌运动a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
(m=0.72kg的动力吸振器的混沌运动a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
变质量m以固定k=10000kn/m3为焦点。图2和图3描绘了庞加莱图中结构响应和非线性能量吸收响应的位移分量。数值结果表明,除了少量的混沌运动外,结构和能量吸收的响应是周期性的。这种混沌运动是由非线性能量吸收器引起的动态复杂性,因为线性结构只具有周期性。对于周期性响应,结构和能量的振动随着能量吸收质量的增加而减小,除了非常小的能量吸收器质量外。应该注意的是能量吸收器的响应似乎比结构的响应更复杂,如图2和3所示。具体地说,图4和图5显示当m = 0.2496 kg时,结构周期性振动,但能量耗散紊乱。图6和图7显示结构周期-1运动,而能量库具有周期-2运动,对于m=0.3384 kg,这一事实意味着能量库出现倍周期分岔,如图3,图8和图9显示振动结构和能量吸收器都可能是混乱的。在上述图中,混沌由时间历程、振幅谱、相位图和庞加莱图来识别,而周期性运动由其局部放大的时程、相位图和庞加莱图来表示。
图10和11给出了在m = 0.5 kg的情况下,当立方刚度k改变时,结构和能量吸收器的庞加莱图中的位移分量的分叉图。 结构和能量吸收器都是周期性地振动,除了对于较小和较大的刚度k的混沌爆发。 结构和能量吸收器的周期性运动的样本分别在图12和图13中示出,并且那些可能是混沌运动的可以在图14和15中找到。可以预期,周期性运动和混沌运动交替发生,以进一步增加刚度。 结构的周期性运动的幅度随刚度增大而增加,而能量库的能量几乎保持不变。
(改变立方刚度k的结构响应的分叉图)
(改变立方刚度k的动力吸振器响应的分叉图)
( k=5600kN/m3结构的周期性振动a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
( k=5600kN/m3动力吸振器的周期性振动a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
( k=14,4000kN/m3结构的周期性振动a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
(k=14,4000kN/m3动力吸振器的周期性振动a时间历史.b时间历史的扩大.c相图.d 庞加莱图)
- 幅频响应曲线:谐波平衡分析
本节从幅频响应的角度着眼于周期性运动。谐波平衡的方法将用于预测在给定频率的激励下的响应。进行谐波平衡分析,等式 (1)被转换为无量纲形式。
(2)
其中结构和能量汇的无量纲位移以及无量纲时间是 (3)
其中l是线性结构弹簧k0/1 kN的静态变形,以及结构频率,质量比,结构和能量吸收器的阻尼比,无量纲的非线性刚度,频率以及无量纲激励振幅分别基于谐波平衡法,控制方程的响应(2)可通过低谐波项的有限和来近似。
(4)
由于该系统的非线性是三次的,因此响应仅包含奇次谐波。在为了检查谐波展开的数值收敛性,考虑了最低的三个奇次谐波,然后响应可以表示如下
(5)
其中 ai j和bi j(i = 1,3,5和j = 1,2)是要确定的相应谐波分量的系数
将式(5)代入式(2)中,并将得到的方程双手的每个谐波cos(igamma;tau;)和sin(igamma;tau;)(i=1,3,5)的系数相等,得到一组非线性代数方程,见“附录a”中的式(A1)。方程(A1)通过使a5 j和b5j(j=1,2)全部为零,导出了一组1阶和3阶谐波平衡系数的方程组,并通过使和(i=3,5和j=1,2)全部为零,进一步简化为1阶谐波平衡系数的方程组。对于给定的参数,公式(A1)和简并情况可通过伪弧长延拓技术进行数值求解。因此,可以得到幅频响应曲线。
( 基于解析和数值方法的能量接收器幅频曲线比较)
(基于不同阶谐波平衡解的能量汇的幅频曲线)
(beta;= 0.125时稳态响应的幅频响应曲线.a结构。 b非线性动力吸振器)
(beta;= 0.0125时稳态响应的幅频响应曲线.a结构。 b非线性动力吸振器)
(lambda;= 63.1579的稳态响应的幅频响应曲线.a结构。 b非线性动力吸振器)
(beta;= 1.25时稳态响应的幅频响应曲线.a结构。 b非线性动力吸振器)
(lambda;=30的稳态响应的幅频响应曲线.a结构。 b非线性动力吸振器)
(lambda;= 160的稳态响应的幅频响应曲线.a结构。 b非线性动力吸振器)
为了描述更高阶的幅频响应曲线,选择一组参数omega;0=28.8675rad/s,lambda;=30,sigmaf;0=0.0017,sigmaf;=0.0017,beta;=1.25,f=0.01,即可计算出响应的均方根。
(6)
(7)
能量接收器的幅频响应曲线如图16所示。由局部放大曲线可知,5阶谐波平衡解与3阶谐波平衡解的计算结果吻合较好,与1阶谐波平衡解的计算结果不一致。具体地说,直到3阶和5阶的解都预测出一个循环,对于gamma;在0.978和0.984之间有一个小间隔,而一阶解决方案无法检测到循环。除了明显的质的差异外,gamma;的附加环在0.978至0.984之间或gamma;的定量差在1.35与1.41之间没有明显的质的差异。在所有情况下,直到第3阶和第5阶的解都是完全一致的,而它们却与一阶解不重叠。因此,谐波平衡直至3阶似乎足够精确。
直接数值积分支持高达3阶的谐波平衡解。 对于omega;0= 28.8675 rad / s,lambda;= 160,sigmaf;0= 0.0017,sigmaf;= 0.0017,beta;= 1.25和f = 0.01,非线性能量吸收器的幅频响应曲线的比较如图17所示。 在这里,为了突出显示两侧的跳跃现象,将lambda;= 30替换为lambda;=160。在正向或反向扫频中,基于直到3阶的解的解析结果(实线)与 数值结果(正向三角形用于正向扫描,而倒三角形用于反向向扫描)。 因此,在下面的研究中,将采用谐波平衡到3阶的方法。
为了检查解的稳定性,
(8)
将响应重新表示为将式(6)代入式(2)将所得方程中每个谐波分量的系数等价于一组非线性微分代数方程,在“附录B”中以等式(B1)表示。等式(B1)的不动点对应于稳态响应。对于给定的参数,可以通过伪弧长延拓技术对不动点进行数值定位。在每个不动点线性化后,将非线性微分代数方程组化为线性微分方程组。每个不动点的稳定性可以由线性微分方程的雅可比矩阵的特征值来确定。这种方法得到稳态响应的稳定性。曲线上可能有Hopf分叉点和鞍结点。在Hopf分叉点,一对复共轭特征值的实部从负变为正(称为第一类型)或反向(称为第二类型)。在鞍点处,正实特征值出现(称为第一类型)或消失(称为第二类型)。
谐波平衡法得到的幅频响应曲线揭示了三次非线性项系数的影响。图18–20描绘了beta;= 0.0125、0.125、1.25时的曲线,而其他参数固定为omega;0= 28.8675 rad / s,lambda;= 48,sigmaf;0= 0.0017,sigmaf;= 0.0017和f = 0.01。黑色实线和蓝色点划线分别表示曲线的稳定和不稳定部分。绿色球和红色三角形分别代表Hopf分叉点和鞍节点。 beta;= 0.0125的情况如图18所示。如图18a所示,结构响应曲线的峰值处存在一个不稳定的开环。该环路从gamma;= 0.996
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[238692],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


