
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
基于III-V铋层衬底支撑的大带隙量子自旋霍尔绝缘体
- E. Padilha,1,* A. Janotti,2,dagger; A. Fazzio,3,4,Dagger; and A. J. R. da Silva3,5,sect;
1Campus Avanccedil;ado Jandaia do Sul, Universidade Federal do Parana, 86900-000 Jandaia do Sul, PR, Brazil
2Department of Materials Science amp; Engineering, University of Delaware, Newark, Delaware 19716-3106, USA
3Instituto de Fısica, Universidade de Sao Paulo, C.P. 66318, 05315-970 Sao Paulo, SP, Brazil
4Centro de Ciencias Naturais e Humanas, Universidade Federal do ABC, Santo Andre, 09210-170 Stilde;ao Paulo, SP, Brazil
5Laboratorio Nacional de Luz Sıncrotron, 13083-100 Campinas, SP, Brazil
我们证明了III-V铋基二维(2D)材料生长在阴离子端接SrTe(111)衬底上是二维拓扑绝缘体。III-Bi层表现出较大的非平凡带隙,从0.15 eV到0.72 eV不等,这取决于顶部表面的钝化,即,使用氢或卤素。我们发现,在SrTe衬底上,由III-Bi层组成的纳米带结构的边缘出现了受时间反转对称性保护的以Gamma;为中心的狄拉克螺旋态。通过对Z2不变式的计算,确定了带隙的非平凡性。我们还发现,在超薄量子阱异质结SrTe/III-Bi/SrTe中,拓扑相保持不变。当二维材料沿[111]方向夹在SrTe之间时,为基于二维量子自旋霍尔绝缘体的纳米结构器件的制备开辟了一条新途径。
一丶介绍
二维拓扑绝缘体(TIs)又称量子自旋霍尔绝缘体(QSHIs),是自旋电子学和纳米电子学的重要材料。这些材料显示了具有锥形能量色散的绝缘体和自旋极化无栅边缘状态。边缘状态受扰动保护,保持时间反转对称性,防止后向散射。量子相变最初是由Kane和Mele[1]在石墨烯中提出的。然而,由于石墨烯中自旋轨道诱导的带隙非常小,预计QSHI相只会在极低温度下发生[2,3],因此很难以可控的方式进行探测。
在HgTe/CdTe量子阱结构[4]中首次发现了QSHI相,但在实际应用中发现的5 meV带隙太小。其他用于QSHI相观察的材料体系也被提出,如硅烯(间隙1.9 meV)[5,6]、锗烯(间隙29 meV)[6,7]、锡烯(0.1 eV)及其卤化形式(高达0.34 eV)[8]。自旋轨道相互作用是TIs的一个关键特征,这引起了人们对铋等重元素作为这些材料的组成部分的兴趣。事实上,Bi负责驱动Bi2Se3和Bi2Te3波段反转的高自旋轨道耦合(SOC)[9-12]。铋层也被提出用于呈现量子自旋霍尔效应[13,14]。
在利用铋作为高SOC强度源的基础上,庄等人提出了III-Bi二元化合物作为一种新型的带隙二维量子自旋霍尔绝缘子。提出了它们的卤化形式[16-18]和氟化PbX二元化合,物据我们所知,由Padilha等人设计的[19]是具有最大非平凡带隙的二维拓扑绝缘子。然而,这些二维QSHIs被认为以独立的形式存在,这在实践中是相当具有挑战性的。二维拓扑绝缘子在保持其拓扑特性的基底上的生长还有待证明,这将为更现实的方法和实际应用铺平道路。
将二维材料支撑在基底上,不仅比二维独立式层更实用,而且可以提供控制拓扑特性的新方法,为器件设计增加灵活性。例如,衬底可以对二维TI施加应变,这允许在二维系统[20]中调整非平凡带隙。然而,也有一些2 d钛衬底之间的相互作用的要求,必须实现为了保持拓扑阶段:底物应该有一个大的带隙,和能带之间的对齐衬底和II型的二维材料应该有效分离的拓扑状态TI和琐碎的衬底。此外,衬底不应诱导二维材料[21]的费米能级附近的金属表面状态。这些要求指向具有非常大带隙的高离子绝缘体作为衬底,因此表面状态只出现在带边缘附近,并且很容易钝化。在这一背景下,Xu等人[22]最近表明,锡烯可以是一个平凡的或量子自旋霍尔绝缘体,这取决于衬底,而其他性质,如Rashba分裂,可以由衬底的晶格参数控制。III-Bi材料以前被提议培养在Si(111)表面[23,24]。在此,我们提出了III-Bi超薄层在SrTe上的生长。SrTe与III-Bi化合物之间的晶格失配较小,有利于生长,而SrTe与Si相比具有更大的带隙,这将避免衬底材料的导电。
在这项工作中,我们证明了生长在阴离子端SrTe(111)上的III-Bi二维材料是二维拓扑绝缘体
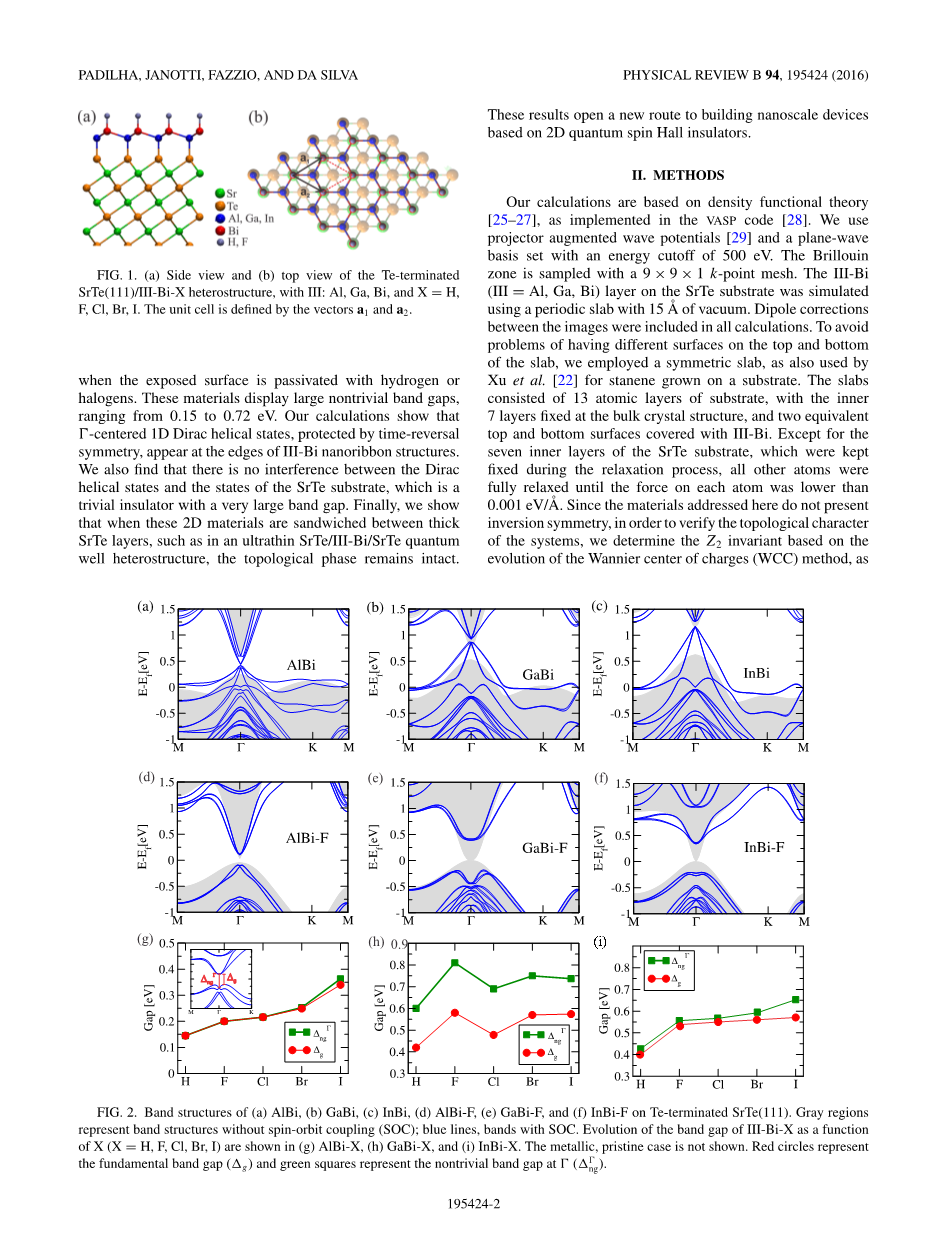
图1所示。(a)和(b)SrTe(111)/III-Bi-X异质结构的侧视图和俯视图,其中III: Al, Ga, Bi, X = H, F, Cl, Br, i。
当暴露表面被氢或卤素钝化时。这些材料显示出较大的非平凡带隙,从0.15 eV到0.72 eV不等。我们的计算表明中心的一维狄拉克螺旋态受时间反转对称性的保护,Г出现在III-Bi纳米带结构的边缘。我们还发现,SrTe衬底与狄拉克螺旋态之间不存在干涉,SrTe衬底是一个带隙非常大的平凡绝缘体。最后,我们证明,当这些二维材料夹在厚厚的SrTe层之间时,例如在超薄的SrTe/III-Bi/SrTe量子阱异质结构中,拓扑相位保持不变。这些结果为构建基于二维量子自旋霍尔绝缘体的纳米器件开辟了一条新途径。
二丶方法
我们的计算基于密度泛函理论[25-27],在VASP代码[28]我们用 中实 现。 我们使用投影仪增强波电位[29] 和一 个能量截止为500 eV 的平面波基集 。采 用9times;9times;1 k 点网 格对 布里 渊区行采样 。III-Bi (III =, Ga, Bi) SrTe 衬底 层是 模拟 使用 周期 板 15Aring;的真 空。 所有计算都包括了图像之间的偶 极子校正。为了避免在板的顶部 和底 部有不同表面的问 题,我们使用了对称板 ,Xu 等人也使用了[22] 对生长在 基材上的锡烯进行了处理 。该 平板 由13 层衬底原子层 组成 ,内 部7 层固定在本体晶体 结构上,上下表面 均覆 盖III-Bi 等效面。 除了第七层SrTe 衬底 的内 部层, 放松 的过 程中 保持 固定, 所有 其他 原子 完全 放松 ,直 到每 个原 子作用力 低于0.001 eV /Aring; 。由 于本文讨论的 材料不存在反演对 称性 ,为了验证系统的拓扑特 征 ,我们根据Wannier center of charge (WCC) 方法 的演化确 定了Z2不变式,即
图2所示。(a) AlBi、(b) GaBi、(c) InBi、(d) AlBi- f、(e) GaBi- f和(f) InBi- f在te端SrTe(111)上的带结构。灰色区域表示没有自旋轨道耦合(SOC)的带结构;蓝线,SOC带。III-Bi-X带隙作为X (X = H, F, Cl, Br, I)的函数的演化过程如(g) AlBi-X、(H) GaBi-X和(I) InBi-X所示。金属的,原始的情况没有显示。红圈表示基本带隙(g),绿色方块表示在(ng)处的非平凡带隙。
图3所示。(a)在kz = 0的互反平面上,跟踪两个平衡点之间的Wannier电荷中心(WCCs)的演化。虚线红色水平线是用来跟踪在布里渊区一半区域内交换的瓦尼尔中心对的数量。(b) InBi-F在没有SOC(左)和SOC(右)的te端SrTe(111)衬底上的s和pxy轨道的投射能带结构。(c) SrTe(111)上InBi-F在没有SOC和有SOC的情况下,导带和价带的s和pxy轨道演化示意图。
由Soluyanov和Vanderbilt提出[30,31]。该方法基于Wannier函数
通过这个方式Z2可以写成
Wannier函数取决于Bloch状态|unk的量规选择。根据Marzari和Vanderbilt对[32]的描述,为了优化Wannier函数的局部化,我们将WCC定义为位置算子的平均值TRIM代表逆时不变的动量,alpha;是占据状态的带指数,Ⅰ和Ⅱ是克莱默的合作伙伴。Z2不变式可由
图4所示。(a)在端te SrTe(111)平板上沉积氟钝化的扶手椅InBi纳米带的电子带结构。我们使用了由7层SrTe和InBi-F组成的有限板。另一边悬空键被氢原子饱和,以防止任何表面悬空键态。(b)对于(a)中所示的每一边缘状态,靠近点的k点的波函数。
计算任意水平参考线的偶数或奇数个交叉点。当WCC演化曲线跨越任意参考线奇数次时,Z2 = 1。对于带状结构,由于有大量的原子和电子,我们使用OPENMX代码[33,34]进行带状结构计算,因为它比VASP计算效率更高,但同样准确。
三丶结果与讨论
在图 1(a) 和图1(b) 中,我们展示了计算中考虑的模型结构的侧视图和俯视图。以岩盐阴离子 端部SrTe(111)为底物。SrTe4.711Aring; 的实验晶格参数,这是接近的平面点阵参数III-B i层[15] 。在独立形式中,只有InBi系统在机械上是稳定的,即在声子谱中没有虚模,而Al和Ga材料则表现出低能量的虚模 。然而,当系统生长在衬底 上时, 这种不稳定是可以避 免的 。我们发现SrTe/III-B i界面的最低能量构型是Te 原子的顶 部有 柱- iii 原子 (如 图1 所示) ,在阳离子位点的顶部有Bi 原子( 如图1 所示) ,如hcp 晶格叠加,结果表明fcc 晶格 层的 能量 增加 了0.05 eV。计算表明 ,这两种界面具有相似的电子性质。 所有其他可能的构型能量都更高 。
AlBi、GaBi和InBi在SrTe衬底上的带结构如图2(a)、2(b)和2(c)所示。阴影区域表示没有SOC的带结构,蓝色线表示打开SOC时的结构。我们注意到,这三个系统表现出半金属性质,在费米能级附近的点附近存在部分占据态。这些状态主要由暴露表面双原子的不饱和pz轨道组成。增加有机碳导致了辐射线分裂,但保留了金属特性。为了去掉不饱和悬空键,我们使钝化暴露表面原子与氢原子和卤素(F, Cl, Br, I)。我们观察氢和卤素原子和Bi原子,形成强大的能带的结合能不同sim;3.0 eV氟碘sim;2.0 eV,不管第三期的元素。这种行为也观察到独立薄膜[18]。氟化表面的能带结构如图2(d) -2 (f)所示。没有SOC,这三种材料都是半金属,价带和导带在(阴影区)接触。当SOC打开时,会出现非平凡的带隙。基本带隙(g)和非平凡带隙(ng)随钝化剂X = H、F、Cl、Br和I的变化情况如图2(g)所示,对于AlBi,图2(H)所示,对于GaBi,图2(I)所示。对于AlBi,基本带隙和非平凡带隙对于所有卤素几乎是相同的,除了碘。
III-Bi层的拓扑性质可以通过一个非零拓扑不变式Z2来确定,这里使用WCC方法计算[30,31]。所有III-Bi系统的拓扑不变式Z2 = 1被确定,其中III = Al, Ga, Bi,被H, F, Cl, Br和i功能化。只有SrTe/InBi-F的结果如图3(a)所示。通过分析布里尤因区两个时反不变动量之间的WCC演化,我们发现WCC总是奇数次越过虚线,令Z2 = 1。
通过对每一种材料的轨道分辨电子带结构的考察,验证了带结构的拓扑性质。在图3(b)中,我们展示了SrTe/InBi-F的轨道投影带结构。没有SOC的s(上)和pxy(下)轨道的投影显示在左边的面板上,我们注意到在这一点附近有一个s-p带反转。当SOC被包括在内时,在费米能级上有一个缺口的开口;s态仍然占据价带,pxy态在导带未占据。在图3(c)中,我们展示了SrTe/InBi-F在费米能级附近,有SOC和没有SOC的电子态的能量示意图。
图5所示。(a)生长在基质上的几种二维TIs异质结构示意图。(b)两个SrTe(111)层之间的InBi原子表示。在没有SOC的SrTe (c)和有SOC的(d)之间,InBi的s和pxy轨道上投射出轨道分辨带结构。
不饱和的金属体系的s和pxy的状态是未占据的。随着F原子与Bi原子成键,s态被填充,pxy轨道被降低到费米能级。当SOC包含在内时,pxy成键态和反键态发生分裂,在Gamma;点。我们检查了,当使用HSE06混合泛函计算进行计算时,s-p波段反演被保留了[35,36]。
二维拓扑绝缘子的一个重要特征是存在奇数个拓扑保护的一维螺旋状磁链边缘状态。当二维拓扑绝缘子与平凡绝缘子接触时,这些状态将导电带和价带连接起来。在图4(a)中,我们展示了一个宽度为sim;10nm的脱离实际的纳米带的带结构,在这里我们可以清楚地看到类似狄拉克的边缘状态。狄拉克态在点附近的空间分布如图4(b)所示。观察能带无限长。随着InBi-F纳米带中单元细胞的渗透,拓扑边缘态分布在边缘附近。状态存在于SrTe衬底中,这是由于人为终止SrTe衬底而产生的悬空键态。
由于边缘相对于纳米带中心对称,狄拉克态是简并的,自旋动量被锁定。边缘状态的自旋投影计算通过自旋极化矢量,,是从头开始布洛赫州,和sigma;=(sigma;x,sigma;y,sigma;
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[430851],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


