
英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
不同强度混凝土结构受弯构件的滞回能量和阻尼力
关键词:超高强度混凝土滞回能粘滞阻尼;延性;塑性铰;
摘要
在刚性框架中,大地震时要在梁端形成塑性铰链,并使它们具有足够的能量和阻尼力来容纳地震能量。对目标混凝土强度为30、70、150MPa 的梁进行了试验研究。其他变量包括:底部/顶部配筋率(0.33和1.0)、横向配筋率(0.8%和1.6%)和剪切跨度与深度比(2.0和3.0)。试验试件的设计是为了表示延性抗弯矩框架中的外梁柱连接性能。梁的顶端受到循环位移的作用,造成明显的非弹性损伤。采用不同的能量和损伤指数来探讨混凝土强度对滞回能量和损伤指数的影响。用等效粘滞阻尼比来计算阻尼。尽管由于混凝土强度的增加,混凝土的脆性增加,但梁的滞回能能力可以通过增加混凝土强度来提高。然而,这种效应不能推广,因为它受到其他变量的强烈影响。通过减少剪力需求,提高底部配筋率,可以显著提高能量承载力,横向钢筋的增加增强了能量损耗的能力,但程度较小。粘滞阻尼比受底部配筋量影响显著,受横向配筋率和抗剪需求水平影响较小。
1、介绍
对于设计为破坏的钢筋混凝土结构不会因为大地震而倒塌,地震造成的能量可以通过迟滞行为耗散。钢筋混凝土构件可以承受重大的地震事件,如果他们可以耗散能量通过滞后而没有相应的强度损失,在一个典型的加载循环中,如图1所示,侧向加载的输入能量应被测试元件吸收。系统吸收能量有两种形式,可回收能量和耗散能量。可恢复能量包括单元保持其原始状态的能力,并包括如图1所示的弹性恢复和非线性恢复。耗散能量是被滞回环所包围的区域,代表了通过钢筋的非弹性行为来减轻地震影响的单元能力,这将导致过度开裂和永久变形。加载循环的耗散能随着损伤程度的增加而减小。如图1中的回路A和B所示。同样的趋势也适用于吸收能源和可回收能源。因此,结构体系的耗能能力是抗震设计和结构评估的首要因素。
评估能量能力的困难可能是由于耗散的能量反映了强度和刚度变化的影响。不同的研究人员针对能量耗散能力提出了不同的能量指标[1-3]。Nmai和Darwin[2]认为能量指数是总耗能与第一次产率消耗能的比值。他们发现,在循环加载下,35的指标值可能提供足够的性能。他们还发现,该指标可以与箍筋强度、剪切需求和混凝土强度相关。他们研究受限于混凝土强度34.5Mpa,最大剪切要求。这些研究都没有考虑到高强度混凝土构造的因素。
由于结构单元的损伤不仅仅是由于滞回作用造成的,Park等人提出了考虑荷载逆转效应和地震最大变形效应的损伤指标。
图1所示。结构元素所经历的能量类型。
Park等人指出了结构的三种损伤状态:当损伤指数小于0.4时,结构是可修复的;如果损伤指标大于0.4,则结构无法修复;如果破坏指数超过1.0,结构就会倒塌。文献中没有迹象表明这些损伤阈值是否适用于用高强混凝土建造的单元/结构。因为Park等人没有根据后一种元素来校准他们的模式。
粘滞阻尼是描述单元在地震中耗散能量能力的另一种方法。对于结构来说,阻尼机构可以用粘性阻尼比来表示。
对于非线性振动结构,黏性阻尼可以用等效黏性阻尼比来计算,它反映了非弹性扰动时结构的损伤程度。定义等效粘滞阻尼比最常用的方法是将实际结构在振动周期中耗散的能量与等效粘滞体系[5]等同起来。由于试样的固有频率不等于激励频率[5],因此在准静态试验条件下使用等效粘性阻尼是一种满意的近似方法。钢筋混凝土构件的阻尼取决于开裂、钢筋屈服和粘结强度钢筋和混凝土之间。未破裂阶段和破裂阶段是不同的,后者包括钢筋与混凝土在滑移过程中的摩擦[6,7].等效粘滞阻尼比随纵筋率的增大而减小,随轴向荷载的增大而增大[8]。
耗散能和等效粘滞阻尼比都可以合理地与相应的位移延性相关联。位移延性是单元变形能力的相对度量,是一个周期内达到的最大位移与第一次屈服时的位移的比值。本文主要研究了耗散能与粘滞阻尼比、粘滞阻尼比、粘滞阻尼比之间的关系位移延性。此外,探讨了混凝土强度、底部/顶部配筋率、横向配筋率、和剪力跨深比,耗散能容量、损伤指数和粘滞阻尼比。
(a)试件的总体布局。
(b)试验样品详情
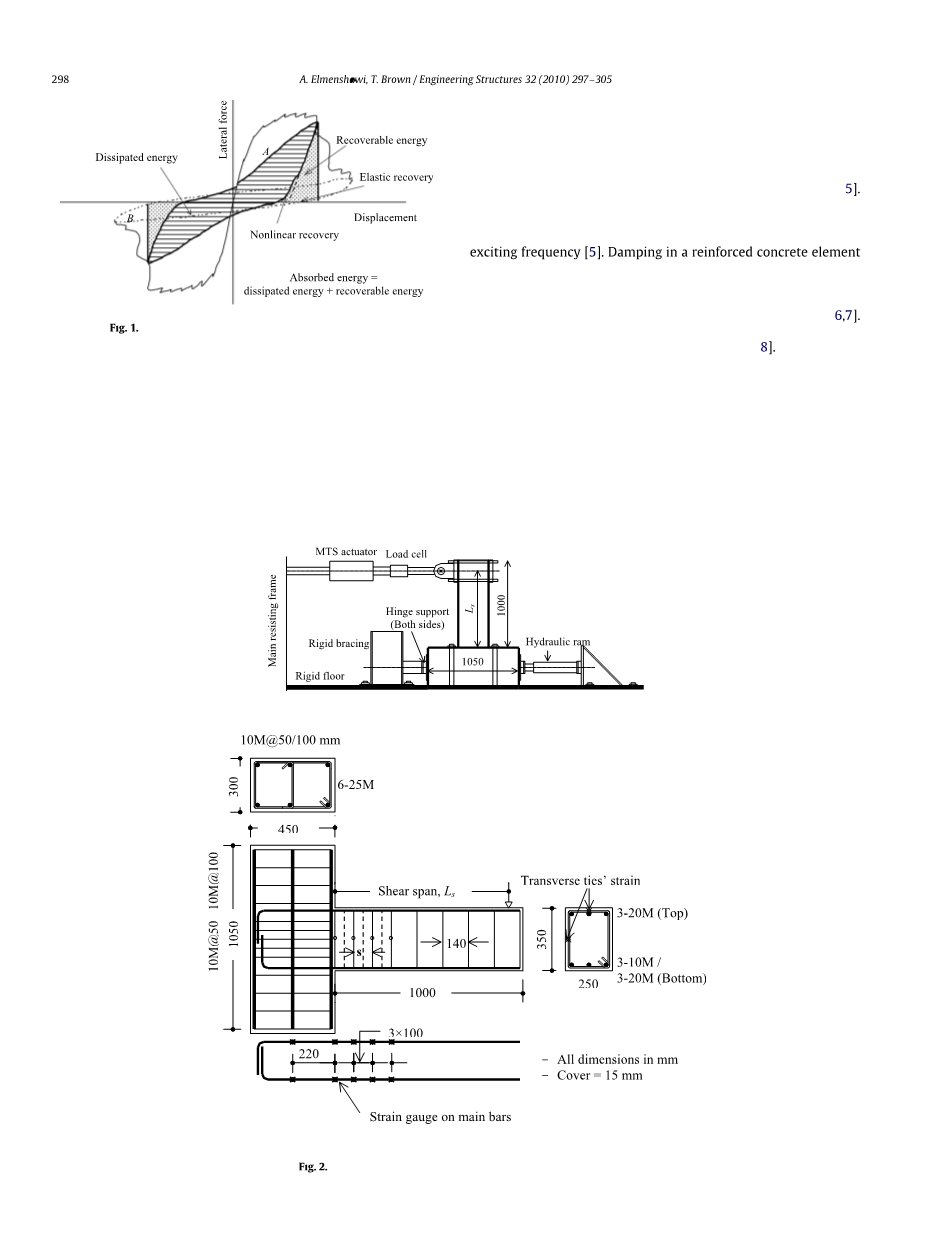
图2所示。试件的试验配置和加固。
表1标本名称及相关变量。
表2试验用钢筋的力学性能
2.测试程序
试件为延性抗弯矩框架内的外部梁柱太阳组合,其塑性变形仅集中在梁端。在整个测试过程中,柱和节点区域都被设计成具有弹性。试件为250x350x1000 mm的整体浇铸梁,柱头为300x450x1050 mm. 如图2所示,将试件安装在柱连接到实验室坚固楼板,梁端连接到执行器水平位移的位置上。试验变量包括混凝土抗压强度、f0,下、上配筋率p0/p,铰区横向配筋率pw,剪切跨深比L如表1所示。目标混凝土强度分别为30、70、150 MPa;虽然获得的优势通常更高。混凝土强度30mpa为普通强度混凝土(NSC);高强混凝土(HSC)为70mpa;超高强度混凝土(UHSC)为150 MPa.底部/顶部钢筋比(p对于高延性单元,0.33的要求该小于地震规范的要求(p/p=0.5),研究混凝土强度的增加是否能补偿能量能力和粘滞阻尼行为。试件设计为挠曲破坏;因此,标称抗剪强度V(只由于横向钢筋)由于受弯V而产生的抗剪强度 从1.12到3.52不等。此外,横向配筋率设计超过ACI 318-08[9]的要求。为满足ACI 318-08[9]对细长梁设计的要求,选择了较低的剪跨比。这样一个较低的剪切跨度与深度比预计代表了一个高剪切需求的情况,因为施加的剪应力将高于对应的更高的剪切跨度与深度比。
试件受准静态位移控制系统的一组增加振幅的循环位移如图3所示。正幅值(顶部受拉)与负幅值(底部受拉)之比取决于两侧抗弯强度之比。因此,对于非对称截面,负振幅与正振幅之比为0.36.钢筋名义屈服强度为400mpa,钢筋的典型应力-应变关系如图4所示。钢筋的力学性能都列在表2中。一个值得关注的参数是f的比值/f(极限强度/屈服强度),达到1.6.f的比值/f抗震设计[9]要求ge;1.25.实验计划的更多细节可以在Elmenshawi[10]中找到。
图3所示。施加于对称试件的指定位移循环。
图4所示。使用钢筋的典型应力-应变行为。
3.迟滞能和损伤指数
对于延性结构来说,在重大地震事件中幸存下来主要取决于它们耗散能量的能力。能量耗散越多,试件性能越好。耗散能量的量度是在图5-7所示的侧向强度-位移关系中,滞回环所包围的面积的总和。图5-7为不同混凝土强度构造的对应梁的滞回图,以及在极限侧向强度V时的损伤状态 如图8所示。值得注意的是,在极限状态之外,并没有形成新的裂缝;然而,现有裂纹逐渐拓宽,形成末端所谓的铰区。图9显示了当前计算中使用的设计。对于非对称截面,将任意周期i的能量分解为Ei 和Ei-,然后求和。能量耗散可以用以下各种指标来评价。
图5所示。试验的横向强度-位移关系No.3
图6所示。试验的横向强度-位移关系No.6
图7所示。试验的横向强度-位移关系No.10.
图8所示。梁在极限侧向强度下的损伤状态。
图9所示。用于能量指标和粘滞阻尼评价的命名。
3.1.累积耗散能量
累积耗散能是指在标称破坏前试件耗散的总能量。当横向强度比极限强度V下降20%时,定义为标称破坏。累积耗散能是指V-8图中封闭面积总和的绝对值。很明显,随着加载周期的增加,累积耗散能量单调增加,如图10和11所示。试验1、4、7对非对称配筋试件的试验结果表明,使用更高的混凝土强度并没有改善能量耗散;特别是UHSC的使用,与NSC相比,UHSC的耗散能显著降低。
HSC和UHSC的使用提高了横向配筋增加的试件的耗能能力(试验2、5和9)/d=2),如图10所示,与对应的NSC和UHSC梁相比,HSC的使用增加了同时实现更多加载循环次数的耗能能力。另一方面,使用UHSC只增加了能量耗散能力,但加载循环次数比对应的NSC梁要少。这些观察结果表明,混凝土强度对耗散能量的影响是由其他试验变量控制的。从图11中可以看出,增加横向配筋、底部配筋和剪切跨可以显著提高能量耗散。
图10所示。高剪切需求试件的累积耗散能。
图11所示。UHSC梁的累积耗散能。
3.2.能量指数
Hwang[1]提出了以下能源指数:
(1)
和如图9所示。索引可以被规范化,允许不同大小和比例的不同标本之间进行比较[1,3],对应于纵向钢筋在受拉时的第一屈服。Hwang[1]报告剪切应力水平、剪切跨深比、箍筋承载力与最大剪切比对值有影响。对于非对称元素,的值和对每个方向进行计算并求平均值。
3.3.能量耗散指数
Nmai和Darwin[2]将累积耗散能相对于屈服的总弹性能归一化,定义能量耗散指数D作为梁在循环荷载作用下的性能判据。指数可以计算为:
(2)
式中:Ecum为累积耗散能,Vy,为受拉时纵筋第一屈服对应的侧向强度和位移,为上底筋比。Nmai和Darwin的耗散能量仅在峰值负载大于或等于初始屈服载荷的75%.题目说0.75的值可以认为是代表梁的可用容量的下限。可以假定,这种对耗散能量的限制忽略了混凝土开裂在预屈服阶段的贡献,并考虑超过当前标称破坏定义的循环,这被认为是试件的最终可用极限。
3.4. 工作指数
Gosain等人[11]建议使用工作指标Iw来评估加载历史的严重性,并比较试件在不同加载历史下的性能。对于整个加载历史,工作索引可以表示为:
(3)
式中,一个循环的最大横向载荷是i,位移与对应。可以看出,功指数不直接表示耗散能,它只考虑包络曲线上的位移和力。然而,功指数可以间接地表示能量,包络曲线表示与耗散能量和损伤相关的进展和退化。Gosain等人[11]只考虑了ge;0.75;然而,他们报告说,这样的限制是任意的。对于目前的实验工作,所有的循环都考虑到公称失效。为了解释小剪切跨度对耗散能的影响,Gosain等人[11]修改了功指数:
(4)
可以近似为剪切跨深比(d=Gosain等人计算的岩心深度)。第二项代表轴向压缩力的作用,在本研究中可以忽略。对于非对称光束,计算了每个方向的信息流及其平均值。
3.5.损伤指数
Park等人[4]提出的损伤指标为地震最大变形损伤与耗散滞回能量的线性组合,如:
(5)
式中:beta;为非负参数,表示强度退化,对于设计良好的钢筋混凝土构件[12],其近似值为0.1,dE为滞回能量增量,其他参数定义如图9所示。
表3试件标称破坏时的性能指标。
图12所示。高剪切要求试件的损伤指数。
3.6.当前结果分析
测试变量对能量趋势的影响(和)和工作指数(Iw和I)检查)。这些指数计算到名义失效为止,列于表3.对于非对称梁(试验1、4和7),混凝土强度的增加使指标值降低。对于腹板配筋增加的梁(试验2、5、9),混凝土强度由NSC增加到HSC,由NSC增加到UHSC,这些指标均有所提高。三种混凝土强度中,HSC的各项指标最高,而UHSC的各项指标均高于NSC.对高剪切要求的梁(试验3、试验6和试验10),与NSC和HSC试件相比,使用HSC提高了指标值,而使用UHSC则降低了指标值。
试件标称破坏时的损伤指数DI的结果(如表3所示)与之前的能量指数对混凝土强度的影响有不同的趋势。对于非对称梁(试验1、4、7),NSC和HSC梁的损伤指标基本相同;然而,UHSC光束明显减少。增大腹板配筋的梁(试验2、5、9),HSC和UHSC梁的损伤指数相同,但均显著高于NSC梁。对于高剪切要求的梁(试验3、6、10),混凝土强度的增加对其损伤指标没有显著影响。为了将损伤指数的值与开裂模式联系起来,我们计算了深蹲梁(试验3、6和10)在极限状态下的损伤指数,如图8所示。可以看出,损伤指数的值非常接近,并且随着试件达到标称失效,这些差异逐渐减小。对于相同的深蹲梁,损伤指数随加载周期的变化如图12所示,表明在相同的加载周期下,损伤指数随着混凝土强度的增加而增加;特别是与UHSC光束相对应的。
能量指数和损伤指数的结果表明,关于混凝土强度影响的具体结论难以表述,因为它们依赖于其他试验变量。试验7~10的结果表明,随着底部配筋量、横向配筋量和剪切跨的增加,各指标均有所增加。
图13所示。能量-容量-位移延性关系。
4.耗散能量-位移延性关系
位移延性mu;为位移的比值位移(纵向钢筋在受拉时的第一次屈服)。本文位移延性计算如图9所示。任何单元的位移延性与耗散能之间的关系是复杂的,因为这两个因素对单元变量的敏感性。在当前的工作中,耗散能量计算到名义破坏,并归一化到总耗散能量在第一屈服E.本文定义的标称破坏极限也被认为是可用的延性极限。标称破坏时,位移延性为.所有试件归一化耗散能与位移延性的关系如图13所示。通过回归分析,关系为:
(6)
如果将4.0的位移延性视为抵御强烈地震所需的最小延性,则相应的标准化耗散能应不小于38.5.令人惊讶的是,尽管在测试变量、回归分析和失效极限的定义上存在差异,但这个值非常接近Nmai和Darwin[2]的极限。该关系式可用于根据ACI 318-08[9]设计的高延性受弯构件的耗散能量估算。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[265150],资料为PDF文档或Word文档,PDF文档可免费转换为Word


