
英语原文共 15 页,剩余内容已隐藏,支付完成后下载完整资料
建筑结构
承压混凝土的有限元建模-I:德鲁克-普拉格型可塑性模型
T. Yu a,JG Teng a ,lowast;,YL Wong a,SL Dong b
a 香港理工大学土木与结构工程系,香港b 浙江大学土木工程系,杭州310027
文章历史:
2008年5月14日收到
收到修改后的表格
2009年11月12日
2009年11月22日接受,在线2010年1月4日可用
摘要
本文首先对现有的Drucker-Prager(D-P)型混凝土可塑性模型使用实验观察结果和数值结果来预测承压混凝土性能的能力进行了严格的审查和评估。该评估表明,要使D–P可塑性模型成功预测FRP约束混凝土和其他被动约束混凝土的行为,需要对其进行修改以使其具有以下三个特征:(a)包括第三偏斜率的屈服准则应力不变 (b)取决于围压的硬化/软化规则;(c)流量规则,该流量规则不仅取决于围压,而且还取决于围封增加率。现有的D–P类型模型均不包含所有这三个功能,因此,不能期望它们能够对主动约束和被动约束(例如FRP约束)混凝土产生准确的预测。然后,本文提出了一种改进的D–P类型模型,其中包括上述所有三个功能。接下来,通过使用改进的D–P型模型获得的数值预测与可用测试结果之间的比较,证明了所提出模型提供主动约束和FRP约束混凝土行为的紧密预测的能力。最后,讨论了所提出的可塑性模型的局限性。通过开发塑性损伤模型可以解决这些限制。然后介绍了包含上述所有三个功能的内容。接下来,通过使用改进的D–P型模型获得的数值预测与可用测试结果之间的比较,证明了所提出模型提供主动约束和FRP约束混凝土行为的紧密预测的能力。最后,讨论了所提出的可塑性模型的局限性。通过开发塑性损伤模型可以解决这些限制。然后介绍了包含上述所有三个功能的内容。接下来,通过使用改进的D–P型模型获得的数值预测与可用测试结果之间的比较,证明了所提出模型提供主动约束和FRP约束混凝土行为的紧密预测的能力。最后,讨论了所提出的可塑性模型的局限性。通过开发塑性损伤模型可以解决这些限制。接下来,通过使用改进的D–P型模型获得的数值预测与可用测试结果之间的比较,证明了所提出模型提供主动约束和FRP约束混凝土行为的紧密预测的能力。最后,讨论了所提出的可塑性模型的局限性。通过开发塑性损伤模型可以解决这些限制。接下来,通过使用改进的D–P型模型获得的数值预测与可用测试结果之间的比较,证明了所提出模型提供主动约束和FRP约束混凝土行为的紧密预测的能力。最后,讨论了所提出的可塑性模型的局限性。通过开发塑性损伤模型可以解决这些限制。
简介
近年来,用纤维增强聚合物(FRP)约束混凝土已成为提高混凝土柱性能的流行技术[ 1 ]。结果,已经通过限制在FRP夹套内的圆形实心混凝土圆柱体的轴向压缩试验对FRP约束的混凝土进行了广泛的研究。现在已经很好地理解了这种均匀约束混凝土的性能[ 2 ],并为此提出了许多应力-应变模型。现有的应力-应变模型包括在closedform表达式面向设计的模型(例如,[ 3 ])和面向对象的分析的模型(例如,[ 2 ,4]),可通过增量过程来预测应力-应变曲线。面向设计的模型基于对实验结果的直接解释和回归分析,而面向分析的模型以明确的方式考虑混凝土和FRP护套的反应以及它们之间的相互作用,并且可以潜在地用于预测混凝土的行为限于其他材料[ 2 ]。现在可以通过以下方式密切预测测试结果:一些现有的应力-应变模型,例如Lam和Teng [ 3 ]以及Teng等人提出的模型。[ 2 ]。相比之下,FRP约束混凝土在圆形截面以外的截面中的行为尚未得到很好的理解[ 5 ]。在FRP约束的非圆形截面(例如矩形截面和环形截面)中,混凝土受到不均匀的限制,并且混凝土的应力变化在整个截面上都很复杂。
除了实验和分析建模之外,还采用有限元(FE)方法对承压混凝土进行建模。FE方法在非均匀承压混凝土的建模中特别有利,因为它能够捕获混凝土中的复杂应力变化。可靠的混凝土有限元建模需要对混凝土使用准确的本构模型。已经提出了许多不同的本构模型用于FRP约束混凝土截面的分析和有限元建模。这些本构模型包括可塑性模型(例如[ 6–22 ])和塑性损伤模型(例如[ 23–26 ])。尽管某些模型[ 23–26包括损坏的弹性,所有这些本构模型都使用混凝土可塑性模型。
尽管先前的大多数研究都给出了有限元分析结果,这些结果在轴向响应应力-应变曲线等总体响应方面与测试结果非常吻合,但这种良好的吻合仅提供了本构模型的准确性和可靠性的必要但不充分的证据。可塑性该模型包含三个截然不同的组成部分:屈服准则,硬化/软化规则和流动规则,所有这些都影响其在预测FRP约束混凝土性能方面的性能。由于抵消了这三个组成部分中的错误,可以对测试结果进行精确的预测。相当不同的可塑性模型会得出类似的良好预测这一事实显然是一个需要澄清的问题。
本文旨在阐明Druker-Prager(D-P)型可塑性模型的三个关键组成部分对其预测FRP约束混凝土性能的影响,并确定D-P可塑性模型必须具备的关键特性。拥有以提供对测试结果的紧密预测。评估集中于d-P型混凝土的塑性模型,因为它们已被广泛使用(例如,[ 6-14 ,18]); 这些模型得出的结论也与其他可塑性模型有关。本文首先概述了承压混凝土的特性,为后续讨论提供了基础。然后,对现有的D-P型可塑性模型进行严格审查并进行数值评估。最后,根据评估得出的结论,提出了一种改进的混凝土可塑性模型,并通过测试结果进行了验证。
2.承压混凝土的性能
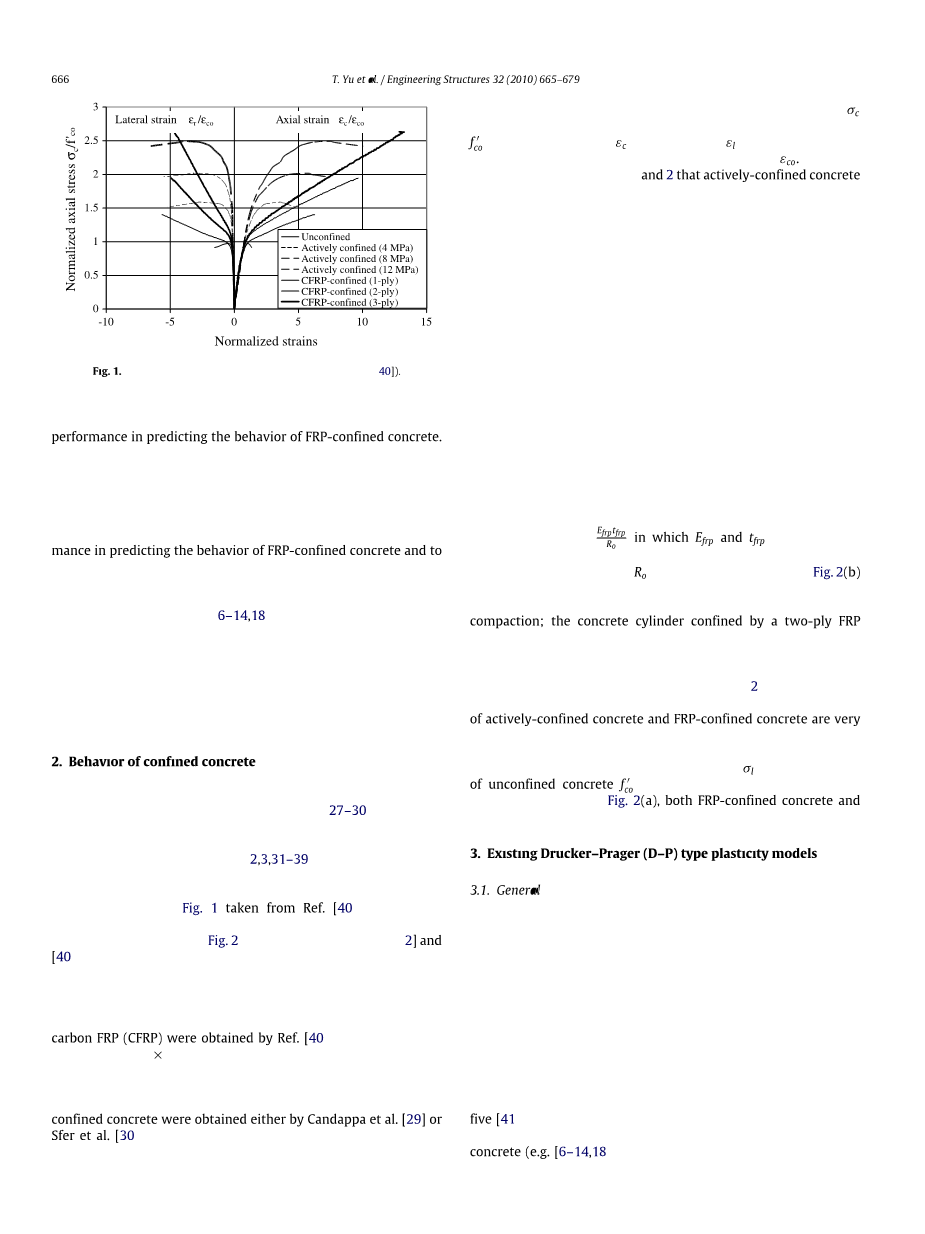
在恒定的主动围压下混凝土的行为已被广泛研究(例如[ 27-30 ])。上FRP约束混凝土,其经受升高的被动围压作为轴向应变增加,广泛的研究也已进行(例如,[ 2 ,3 ,31-39 ])。为简单起见,除非另有说明,否则术语“ FRP约束混凝土”在此后仅保留在装有FRP护套的圆形实心圆柱中。图1 摘自Ref。[ 40 ]分别显示了主动约束和FRP约束混凝土的一些典型应力-应变曲线,图2 (a)和(b)取自Refs。[ 2]和[ 40 ]分别示出了两种类型的承压混凝土的膨胀特性。在这些图中,将压缩应力/应变定义为正,而将拉伸应变/应力定义为负。除非另有说明,否则本文通篇均采用这些定义。碳纤维增强混凝土(CFRP)约束的混凝土的曲线由参考文献1获得。[ 40 ]来自对分别限制在一层,两层和三层FRP护套内的152 mm times; 305 mm混凝土圆柱体进行的压缩测试。CFRP的标称厚度为每层0.165毫米,弹性模量为250 GPa,拉伸强度为3800 MPa。活性约束混凝土的曲线由Candappa等人获得。[ 29]或Sfer等。[ 30 ]来自具有不同侧向压力(例如4 MPa,8 MPa和12 MPa)的主动约束的混凝土圆筒。这些标本的无限制混凝土圆柱强度在32.8 MPa至42 MPa的范围内。在这些图中,轴向应力sigma; Ccedil; 由无约束混凝土的抗压强度归˚F 共 0 而轴向应变ε Ccedil;或横向应变ε 升 由无约束混凝土的轴向应变在其峰值应力标准化ε CO。
从图2和图3 可以看出。1 和2主动约束混凝土具有以下性能:(1)随着围压的增加,混凝土的峰值应力及相应的应变增大;(2)受较大围压限制的混凝土轴向应力-应变曲线的下降分支逐渐增大;(3)对应于相同的轴向应变,在较大围压下混凝土的横向膨胀较小;(4)主动密实混凝土在体积压实后表现出连续的体积膨胀,过渡点的体积应变随围压的增加而增大。从简单的计算中还可以发现,与第二偏应力不变式的峰值直接相关的混凝土的抗剪强度随着围压的增加而增加。
FRP约束混凝土的主要特征包括:(1)如果FRP护套相当坚硬,则近似双线性的轴向应力-应变曲线,其第一部分与未约束混凝土的曲线仅略有不同,而第二部分取决于玻璃钢护套的周向刚度和强度;(2)在相同的轴向应变下,由较硬的FRP护套约束的混凝土的横向应变较小;及(3)体积变化显著在FRP套刚度取决于Euml; FRP ř ouml; tfrp其中euml; FRP和 吨FRP分别在圆周方向上和FRP护套的厚度的弹性模量,和R o是圆柱体的半径。图2 (b)表明,由一层FRP夹套约束的混凝土圆柱体在压实后呈现出不断增加的体积膨胀。由两层FRP夹套约束的混凝土圆柱体在开始时具有体积密实性,然后体积膨胀,在最后阶段减小,直到最终破坏。由三层FRP护套约束的混凝土圆柱体具有连续的体积压实。滕等。[ 2]还从测试结果得出结论,尽管主动约束混凝土和FRP约束混凝土的侧向应变-轴向应变路径有很大不同,但在给定的侧向应变下,轴向应变主要(如果不完全)取决于所定义的当前约束比作为横向围压之间的比率sigma; 升 和无约束混凝土的强度˚F CO 0 。该结论意味着在图2 (a)的截取点处,FRP约束混凝土和主动约束混凝土都具有相同的约束比。
3.现有的Drucker-Prager(D–P)型可塑性模型
3.1一般
混凝土可塑性模型通常基于金属的可塑性理论的相同框架,但是需要进行必要的修改以包括混凝土的独特特性。可塑性模型的关键方面包括屈服面(包括初始屈服面和后续屈服面),流动规则以及硬化/软化规则。初始屈服面决定了何时开始塑性变形。流动规则决定塑性变形的方向;硬化/软化规则定义了屈服面如何随着塑性变形而演化。
已经提出了许多针对混凝土的屈服函数。这些函数中包含的参数数量范围从一个(例如,最初为金属开发的Von Mises准则)到五个[ 41 ]。在这些屈服函数,德鲁克-普拉格(d-P)标准已经被广泛用于约束混凝土(例如,[建模采用6-14 ,18 ,因为它简单])(仅涉及两个参数)和它的能力,以捕获剪切强度。
由于静水压力的增加而增加,这是受约束混凝土的独特性能。D–P屈服准则和压力不敏感准则radic;(例如Von Mises准则)之间的差异在应力空间的I 1 - J 2平面上很明显(图3)。)。后者是平行于横坐标的线,而前者是倾斜线。当可塑性模型基于D–P屈服准则时,它被称为D–P型可塑性模型。在本节中,将通过检查上述三个关键方面(即屈服准则,硬化/软化规则和变形)来讨论这种模型对主动约束和FRP约束混凝土行为的仿真能力。流规则。各种现有d-P型模型[ 6-14 ,18 ],其主要特性总结在表1中,进行检查。引入了一些数值测试来评估其性能。在本文的审查过程中,又发布了两个D–P型模型[ 20 ,21 ]。表1 还总结了它们的关键特性,并在适当的情况下在文件中讨论了它们的性能。本文提出的数值测试是使用ABAQUS进行的[ 42 ],所有用于混凝土的D-P型模型都在ABAQUS的扩展Drucker-Prager模型的理论框架内,本文稍后将对其进行详细介绍。有限元模型的目的是预测承压混凝土的轴向应力-应变和横向膨胀行为。因此,对于在均匀主动围压下的混凝土,仅使用单个8节点实心单元;对于由圆形FRP护套限制的混凝土,仅垂直切片的四分之一使用混凝土的单层8节点实心单元与FRP护套的4节点壳单元绑在一起,对测试样本进行建模。
3.2屈服准则
3.2.1一般方程
所述d-P屈服准则的形式如下[ 14 ,41 ]。
其中theta;和k为待确定参数,J 2和I 1 分别为第二偏应力不变和第一应力不变。当k不是常数并且与塑性变形有关时(等式(2)),它被称为硬化/软化函数和等式。代表初始和后续屈服面。
其中d ε〜p是等效塑性应变增量。当采用具有相关流动规则的D–P屈服准则时,对于三轴压缩下的混凝土,C p由以下方程式表示:混凝土在两个横向方向上承受相等的主应力,在轴向方向上承受主应力Ccedil; p可以将经典金属塑性模型视为D–P型模型的特例,其中theta; = 0,因此C p 。
从等式可以明显看出。(1)假设theta;是给定材料的常数,则初始和后续屈服面在应力空间中具有相同的形状。随后的屈服radic; 曲面是I 1 - J 2平面中的一系列直线。这些线均与表示初始屈服面的线平行,如图4 所示。这些线之间的唯一区别是与J 2 轴的截距的radic;点,并且该截取点取决于硬化/软化功能k。破坏面在随后的屈服面中,并且具有最高的k值。从等式也可以看出。(1)D–P屈服面在偏斜面上呈圆形,如图5 所示。
3.2.2观察结果
在等式中 在(1)中,theta;被称为摩擦参数。theta;的值可以从三轴压缩下混凝土的经验公式推导出。在许多这样的方程式中,最流行的是Richart等人提出的那些。[ 27 ]和Mander等人。[ 2 ]最近提出了一个已经通过大量测试数据验证的方程。使用Richart等人提出的方程,发现摩擦参数为0.2934。[ 27 ]和使用腾等人提出的方程为0.2634。[ 2 ],如附录A中所述。
它已被许多研究人员指出(例如,[ 8 ,25 ,41 ]),其具体的下等于双轴压缩剪切强度,这是指在两个主方向上进行相等的应力混凝土和零张应力在第三主方向,即使两种情况的第一应力不变性相同,三轴压缩下的应力也不同。根据可塑性理论,已知混凝土在相等的双轴压缩和三轴压缩下的应力状态对应于偏斜面上的不同圆周位置(图5)。)。这两种情况之间的抗剪强度比(即相等的双轴压缩和三轴压缩)可以从实验结果或经验公式中找到,在相等的双轴压缩和三轴压缩下混凝土的强度(请参见附录B )。如果Kupfer等人的实验结果。[ 43 ]用于等轴压下的混凝土和Richart等人提出的经验方程。[ 27 ]用于三轴压缩下的混凝土,该强度比约为0.7(附录B),远小于圆形破坏曲线所暗示的1。因此,破坏面,其目的是反映混凝土的试验行为应该考虑到所述第三偏应力不变的效果,并采用在偏平面[非圆形的故障曲线7 ,18 ,21-23 ]。这种故障表面的可能形状在图5中示出。
3.2.3。评估现有模型
Karabinis和Kiousis [ 6 ],Mirmiran等。[ 11 ],Shahawy等。[ 12 ]
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[246487],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


