
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
示例12.9端块加固设计(加固)
图12.17中的梁端受到四个相同的100 毫米圆锥形锚固件的应力如图所示,每一个都施加了400 千牛的顶推力。
该区域可细分为四个相等的端部区域,分别为侧面200 150毫米(图12.7a),即
2y0= 200毫米(垂直方向);
= 150毫米(水平方向);
图12.17
等效的方形锚固边2== 88 毫米。因此垂直方向上,
==0.44;
因此,来自表12.1
= 4000.188 = 75.2 kN;
在端面200毫米范围内用垂直钢抵抗;并且在水平方向上
==0.59
因此来自表12.1
= 400times;0.188 = 57.2 千牛
在端面150 毫米范围内用垂直钢抵抗。
然后使用= 460 牛/ 的高屈服强度钢来粘结筋,
许用应力= 200牛/
因此,需要75.2 千牛的力。
三个合适的10毫米的闭合连杆(471),例如距端面50、100和150毫米
检查水平面,两个连杆位于端面150毫米以内,从而满足要求。
考虑锚固的组合效应= 4times;400 = 1600 千牛
每侧端块=每条400毫米(图12.17b)
等效锚固面的边== 176毫米
因此
==0.44
并且
= 1600times;0.188 = 301 千牛
从超过端面400 mm范围内用垂直钢抵抗。
在距端面50毫米的中心处提供七个的12毫米连杆(1584 毫米2)。
12.5极限极限状态下的分析和设计
在设计预应力构件以满足可使用性要求之后not;。必须进行检查以确保抵抗的最终时刻not;强度和抗剪强度足以满足极限极限状态的要求。进行此分析时,载荷和材料安全的部分因素为极限状态的正常值,该值在第2章中给出。
12.5.1节点分析
当预应力构件上的载荷增加到工作值以上时,会发生开裂,并且预应力钢开始表现为常规的钢筋。构件的极限性能与普通钢筋混凝土构件完全相同,只是计算中必须考虑钢中的初始应变。可以通过使用第4章中所述的等效矩形应力块来轻松分析该截面。BS 8110包含允许最终施加预应力钢中应力的表格,以及相应的表格。not;矩形截面要获得的中性轴位置。这些基于经验结果,但是可替代地,示例12.10中所示的简化方法可用于粘合构件。
当预应力构件上的载荷增加到工作值以上时,会发生开裂,并且预应力钢开始表现为常规的钢筋。构件的极限性能与普通钢筋混凝土构件完全相同,只是计算中必须考虑钢中的初始应变。可以通过使用第4章中所述的等效矩形应力块来轻松分析该截面。BS 8110包含允许最终施加预应力钢中应力的表格,以及相应的表格。not;矩形截面要获得的中性轴位置。这些基于经验结果,但是可替代地,示例12.10中所示的简化方法可用于粘合构件。
尽管通过简单的示例示出,但是该方法可以应用于可以具有预应力线或筋的任何布置的任何形状的横截面。如图12.18所示,使用了预应力钢的应力-应变曲线。计算每层钢的拉力。钢的总应变是由于预应力而增加到钢中初始应变的弯曲所导致的应变。对于一系列假定的中性轴位置,将总拉伸能力与均匀应力0.45扇形所产生的压缩力进行比较。当获得合理的一致度时,可以评估阻力力矩。
应力
牛/毫米2
应变
图12.18预应力钢的应力-应变曲线
例12.10电阻极限矩的计算
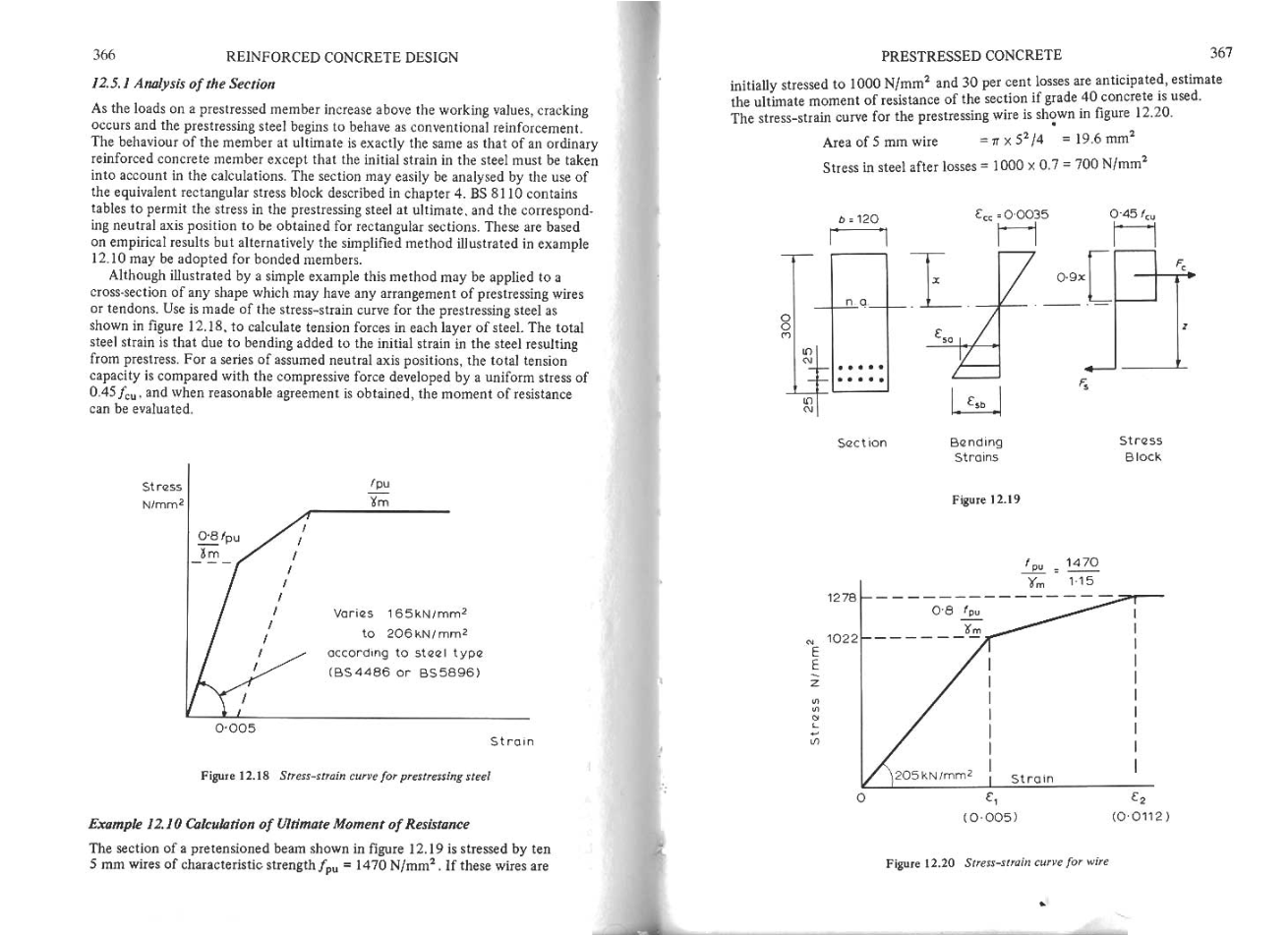
图12.19中所示的预张紧梁的截面由特征强度= 1470 牛/ 毫米2的十根5 毫米钢丝施加应力。如果这些电线是初始应力为1000 牛 /毫米2,预计会损失30%,如果使用40级混凝土,则估计断面的极限抗弯矩。预应力钢丝的应力-应变曲线如图12.20所示。
5毫米钢丝截面积==19.6毫米2
损失后的钢应力= 1000times; 0.7 = 700牛/ 毫米2
应力块
截面
弯曲应变
图12.19
图12.20 导线的应力-应变曲线
因此
损耗后的钢应变= =0.0034
小于,屈服应变较低。
必须找到中性轴的深度x,混凝土中的压缩力Fc与钢中的拉伸力平衡。然后,抵抗的最终时刻为
(12.31)
其中z是和之间的杠杆臂。
第一次尝试x= 130 毫米,大约等于0.5d。
(a) 钢应变
最终钢应变=预应力应变 弯曲应变
(在计算时,由于预应力引起的初始混凝土应变可以忽略不计。)
顶层
=0.0034
因此 = 0.0034 (12.32)
=0.0034
=0.0066
底层
=0.0034
= 0.0034 (12.33)
=0.0034
=0.0073
(b) 钢应力
根据应力-应变曲线,相应的钢应力为
顶层
= 1022 (-0.005) (12.34)
=1022 41290(0.0066 - 0.005)
= 1088牛/ 毫米2
并且
= 1022 41290(-0.005) (12.35)
=1022 41290(0.0073 - 0.005)
= 1117牛/ 毫米2
(c) 钢和混凝土中的力
钢拉力= (12.36)
= (1088 1117) 98
= 216103 牛
带矩形应力块
混凝土压缩力 (12.37)
牛
混凝土中的力大于钢中的力,因此必须尝试较小的中性轴深度。
表12.2给出了中性轴进一步试验深度的计算结果。对于x = 110,Fc变得小于,因此尝试了x = 120和116,然后发现=
|
张力 |
压力 |
力 |
||||
|---|---|---|---|---|---|---|
|
X |
|
|||||
|
(mm) |
() |
(N/) |
(kN) |
|||
|
130 |
6.6 |
7.3 |
1088 |
1117 |
216 |
253 |
|
110 |
7.8 |
8.6 |
1138 |
1171 |
226 |
214 |
|
120 |
7.2 |
7.9 |
1113 |
1142 |
221 |
233 |
|
116 |
7.4 |
8.2 |
1121 |
1154 |
223 |
225 |
表12.2
就钢中的拉力而言,截面的极限抗力由下式给出:
如果x被错误地选择为130 毫米,则使用公式12.38将等于44,1 千牛米。或以混凝土的形式
将(= 47.5)这两个值的平均值与正确答案进行比较,可以看出,中性轴位置的微小误差不会对计算出的计算矩产生任何重大影响。
12.5.2 附加钢筋设计
如果发现(如2级或3级构件的情况)未达到极限状态要求,则可以添加其他未张紧或部分张紧的钢以增加极限抗弯矩。
例12.11未张拉钢筋的设计
对于图12.21所示的矩形梁截面,设计无张力的高屈服钢筋(= 460牛/毫米2),如果5毫米电阻的极限弯矩超过40 ,则用5根5毫米电线施加力50级混凝土。张紧钢的特性强度。 = 1470牛/毫米2
(a) 检查抵抗的终极时刻
如果是预应力钢,则产生最大拉力
要平衡的混凝土抗压面积
因此,中性轴深度x= 51 毫米。
假设如示例12.10中所计算的那样,
总应变=预应变 弯曲应变
=0.0034
=0.0034
杠杆臂 =
因此
极限力矩=
因此,需要不张紧的钢以允许梁支撑40的极限力矩。
需提供的附加力矩 = 40-31.5 = 8.5
附加钢的有效深度 = 245毫米
然后
杠杆臂附加钢210毫米
然后
所需的附加张力= = 40.5 千牛
压力块
弯曲应变
截面
因此
未张拉的钢的估计面积需要达到屈服应力
尝试使用两个直径为10毫米的钢筋(157)。
(b)检查钢应变
如果产生了额外的钢材,则以两个T10钢筋为力
因此,如果所有钢都屈服,则总拉伸力= 125 62.8
=187.8千牛
从而
极限处的中性轴深度=
因此
预应力钢应变
而且
未张拉的钢应变
该值大于4.1.2节中的0.002屈服应变。
(c) 检查抵抗的终极时刻
花点时间围绕压缩中心
如果在(b)中发现预应力钢或未张紧钢都没有屈服,则将需要类似于示例12.10的反复试验方法。
12.5.3 剪力
预应力混凝土中的剪切力被认为是极限状态。因此,剪切设计涉及最严酷的载荷条件,并结合了极限状态下载荷时通常的部分安全因素。
构件抵抗剪力的作用与钢筋混凝土相似,但由于预应力而具有压缩的附加作用。因为设计是基于限制混凝土中对角线主拉伸应力的,所以这将大大提高抗剪强度。
尽管大多数预应力混凝土构件在工作载荷下不会破裂,但在承受极限状态的载荷时,它们很可能会在部分跨度上破裂。这将降低剪切能力,但幸运的是,简单支撑的构件中的裂纹区域通常将是跨度的中心部分,其中剪力相对较小。
完整的部分
在未开裂的截面上,如图12.22所示的梁单元的莫尔圆分析,其经受了纵向压缩应力和剪切应力合作,得出的主要拉伸应力为
可以重新排列以产生剪切应力
图12.22
可以看到梁在任何水平受到剪切力V的实际剪切应力为
其中是该截面上围绕光束的质心轴的那部分的面积的一阶矩,如图12.23所示,b是该截面在所考虑的高度的宽度,I是第二个整个截面围绕其质心轴的矩。
因此,如果是主张力的极限值,则未破裂部分的极限抗剪强度将变为
对于矩形截面,最大切应力出现在质心处,因此,然后
并且
得出
横截面
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[237004],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


