
英语原文共 15 页,剩余内容已隐藏,支付完成后下载完整资料
边坡稳定桩与群桩:参数研究与设计见解
R.Kourkoulis; F.Gelagoti; I.Anastasopoulos; and G.Gazetas, M.ASCE
对于相对较小的桩埋距,桩效应是由没有实质性弯曲变形的刚体转动控制的:失败的短桩模式。这些情况下,桩的结构能力不能被利用,设计不合算。研究发现,关键的要达到不变性条件的基础埋置深度从0.7到1.5不等,取决于不稳定地面与稳定地面的相对强度的比较(例如:滑动平面下的土),无量纲设计图表的例子提出桩嵌在岩石中,结果提出了两种典型的长细比和几种桩距。单桩的结论一般不适用于稳定深层滑坡,尽管利用框架来限制群桩的手段可能会提供一个有效的解决方案。DOI:(能源科学技术)10.1061/(第3期)gt.1943-5606.0000479. copy;2011美国土木工程师协会
CE 数据库主题词:边坡稳定性;嵌入体;群桩;参数
关键词: 边坡抗滑桩;嵌入深度;简化法;无量纲表; 成拱作用;群桩
导言
用桩来稳定边坡是被广泛接受和成功应用的方法(Heyman 和Boersma,1969;Drsquo;Appolonia 等, 1967)显存的设计方法可以分为压力或基于位移法(De Beer 等,1972;Ito 和Matsui 1975;Poulos 1995)和 数值法(Oakland 和 Chameau 1984;Poulos 和Chen 1997)。在第一种情况下,桩是受到假定的边坡位移。因此,必须指定,随着桩土接触压力深度的分布。在第二种情况下(即:数值方法),问题是采用有限元素或有限的差异来分析的。目前这些方法可以解决整个三维(3 d)问题,考虑到具体的几何、土壤结构相互作用和群桩效应。虽然这些方法在原则上是最严格的,但是3 d应用程序是计算密集型和耗时的。
Kourkoulis等人提出了边坡抗滑桩的一种混合设计方法并做了彻底验证。(2010))在解耦方法的基础上(Viggiani 1981;Hull1993;Poulos 1995,1999),结合被广泛接受的简单性分析技术和3 d有限元(FE)建模的优势,该方法包括两个步骤。
步骤1:执行传统的边坡稳定性分析(如:使用Bishop(1955),Janbu(1957),Spencer(1967),或Sarma(1973))法来计算用来增加边坡的安全系数以达到期望值所需的侧阻力(RF)。
步骤2:选择一种桩结构能够提供所需的RF(增加边坡的安全系数以达到所需的级别)规定的变形量。
第二步提出了种新颖的方法,从桩侧容量的计算解耦边坡几何结构,从而对桩周围的土壤的有限区域数值模拟。目前的文章参数使用这种解耦分析方法获得关于桩及群桩的反应影响因素的见解。无量纲设计图表就是为了当作一个具体的例子来说明该方法在实践上的有效性。
桩侧能力的解耦方法
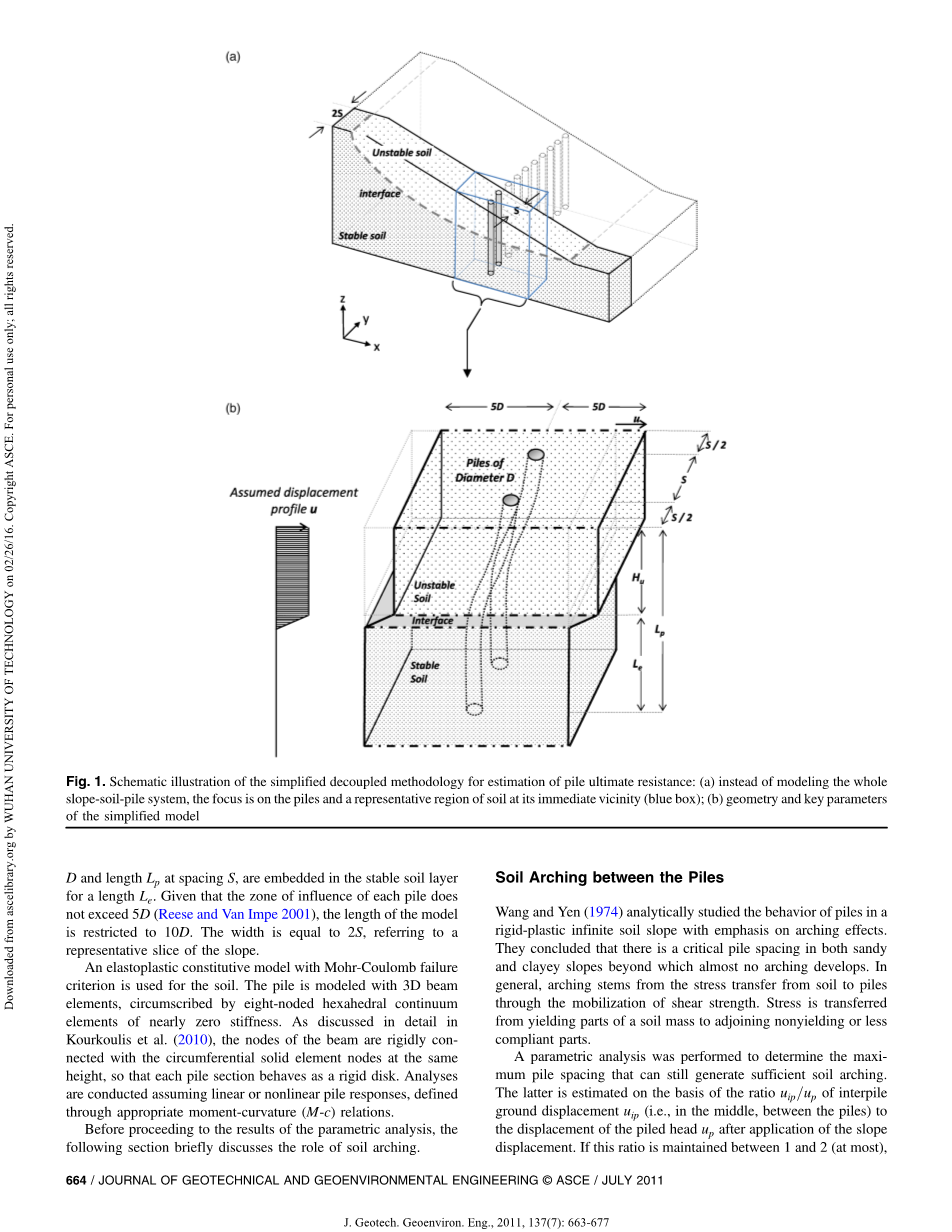
如图1示意的,第2步主要关注桩周围地区的代表土壤,而不是建立整个边坡-土-桩系统的模型。极限强度(或阻力)是通过在模型的边界上加设统一的位移简况来计算的,这是一个合理的简化(如Poulos(1999) 和 Kourkoulis et al.(2010)演示的那样)。排除详细的边坡几何滑动界面,FE模型中指定深度 的滑动面;一定直径D和间距长度 的桩,以一定长度嵌入到稳定土层。鉴于每个桩的影响区不超过5D(Reese 和 Van Impe 2001),模型的长度被限制为10 D。宽度等于2S,指的是边坡的代表性部分。
利用了摩尔-库仑抗剪强度破坏准则的弹塑性本构模型被用于土壤。用3D梁元素建模的桩,被几乎零刚度的八节间六面体的连续的元素限制了。正如Kourkoulis et al. (2010)详细讨论的那样,梁的节点与周围土单元刚性连接在同一高度,这样每个桩都部分充当一个刚性圆盘。通过适当定义弯矩-曲率 (M-c)的关系,进行假设线性或非线性桩响应来分析。
在得到参数分析的结果之前,以下部分简要讨论了土拱的作用。
图1.桩极限阻力估计简化解耦方法的示意图:(a)代替整个边坡桩土系统的建模,重点是对桩和在其附近土壤的特征区域(蓝色框);(b)几何和关键参数
桩间的土体拱起
Wang and Yen (1974)分析研究了强调拱效应时,在刚塑性无限土边坡中桩的行为。他们得出的结论是,仅沙质和粘土质斜坡有一个关键的桩间距,除此以外几乎不会起拱。一般来说,拱起来自土壤的压力,通过剪切强度的转移,转移至桩。压力从土体的屈服部分转移到邻近的刚性或刚性较强的部分。
进行参数分析,以确定的最大桩间距使之仍能产生足够的土拱。后者在桩间地面位移(例如,在中间,在桩之间)与在边坡位移应用后的桩头位移的比率的基础上进行的。 如果这个比例是1和2之间保持(最多),桩和桩间土以近相同的数目置换,可以认为是从拱效应。至于更高的比率,拱效应降低。Prakash (1962),Cox et al.(1984),Reese et al.(1992)的研究发现验证了数值结果,并且根据梁、曾(2002)的研究,桩间距S5D必定产生一个群体效应与桩间土拱。S>5D,桩的行为几乎与单桩一致,土壤在它们之间流动。因此,这样的安排不能应用于边坡稳定,并且不能进一步研究。如下面的详细说明,S = 4D可以被认为是最具成本效益的安排,因为当桩间土适当保留时,它是可产生桩间土拱的最大的间距(即最小种群桩)。这是与工程实践中常见的(S = 4D间距作为边坡稳定应用的的最佳桩间距)和众多的研究成果(Smethurst and Powrie 2007;Pradel and Carrillo 2008)均一致。
图2提供了两种极端情况之间的一个说明性的比较:在桩间距S = 2D这种非常密集的结构,其中土拱是有保证的,和大间距S = 7D稀疏结构,其中桩相隔甚远,他们之间的土壤流动(即,没有拱发展)。不稳定的土层被视为是一种松散的粉砂:and 。稳定(底)层是非常坚硬的土壤,,与软岩接壤。这边界,表示边坡的滑动平面,位于的深度,其性质是和。图2(a)绘制了D=1.2m 和 S=2D情况下的地表位移等值线。位移等值线的分布表明,桩间土取代了几乎同样数量的桩(即),这是一个强拱效应十分明显的体现。形成鲜明对比的是,S = 7D的情况下,桩间土几乎是由桩和土间流动来限制:基本上大于[图2(b)]。
图2.桩间土拱;水平位移等值线图(已经准备网格几何让两桩可以在中央部分;这里介绍的情况,这些元素表示土的性质):(a)密桩结构(S = 2D);(b)疏桩结构(S = 7D)
参数分析
下面是所讨论问题的详细参数分析的结果。粘性土都被用于模拟不稳定层。从表面的界面深度也是变参数的,从4-12m:,分别为浅层和(相对)深层滑动。讨论如下关键反应因素:
- 非线性桩的影响;
- 桩间距的影响;
- 不均匀土层的不稳定性;
- 稳定土层的强度,和
- 桩嵌入到稳定层的深度。
桩结构非线性的影响
同样的土和桩结构的例子,非线性指的是钢筋混凝土桩的非线性。这是通过适当的横截面的弯矩曲率关系的有限元分析,计算的配筋比例为4%。这一选择是基于初始敏感性分析,揭示了最具成本效益的解决方案是,安装的最小量的桩而最大可达到的加固。虽然规范允许配筋数量增加,但无疑会导致钢筋笼相当密集,所以在实际应用中, 2-3%的配筋率通常是极限。因为桩弯矩能力取决于其直径和配筋率,减少钢筋将需要增加桩径以保持其弯矩能力不变。表1总结了配筋率对一些典型的桩尺寸桩弯矩承载力的影响,通过采用XTRACT 软件部分分析计算钢筋混凝土(C30,S500)。表1结果表明,对典型案例研究,直径D、4%配筋率的桩,与配筋率3%、直径1.1D的桩,或直径1.2D(1.2m)、2%的配筋率的桩产生大致相同的力矩。因此,在以下给出的结果(指配筋率4%),可以概括为低配筋率。
注明:混凝土强度C30,钢铁强度S500
表1不同桩径和配筋率的桩身弯矩承载力
图3比较了弹性桩和非线性桩的响应,都受到侧向位移,有两种滑动类型:一个浅层(= 4m)和较深层(= 8m)的滑动。在浅层滑动中[图3(a)],土壤破坏支配系统的行为;得知= 4m不足以驱动桩结构达到极限承载力。因此,桩的非线性并不重要。相反,对于深层滑动( = 8m),差异很明显[图3(b)]。现在,流土深度足够对桩结构施加一个足够大的推力使之达到极限承载力。而且,只要桩未达到其屈服曲率,响应不受桩的无伸缩性的影响。因此,这些参数的分析假定为弹性桩响应;结果大致适用于非线性桩,只要它们没有达到它们的极限曲率。
图3:桩的非线性效应;桩射频RF与桩头位移和非线性弹性桩最大弯矩M有关:(a)浅层滑动,=4m;(b)相对深层的滑动, = 8m
桩间距的影响
图4说明了各种桩间距滑动深度的影响:浅层(= 4m)和深层(= 8m)滑动,以及中间的案例(= 6m)。结果适用于前面的桩土结构(D= 1.2m桩在理想化的松散粉砂)的桩。桩埋置长度等于不稳定土层厚度(相当于稳定地层中完全固定条件的桩)。以下的趋势是值得注意的:
- 桩间距越小,单位宽度提供的力越大。尽管桩间距减小 增加了每单位宽度的阻力,其有效性(即,每一桩的阻力)是由于桩的相互作用而降低的(即,群桩效应)。
- 随着间距的增大,桩身位移要产生一个特定的射频增量。虽然它可能误导总结出所有的结构可以提供大致相同的极限的力的结论(在每种情况下发展不同的水平的移),但这只是弹性桩才有效。如果考虑桩的极限结构能力在内 ,最终的射频很大程度取决于桩间距,即使没有限制容许位移。为了进一步阐明这点,图4(b)中的虚线显示的D = 1.2m桩极限弯矩,这大约是7.2MNm(包括4%可能的最大增量)。它的交叉点与RF 曲线对应的最终真实的R,可以由各自的桩结构提供。显然,R(根据每单位宽度的阻力)随桩间距S的减小而增大:针对于S = 2D,3D,4D,分别是 R 960,740,和570kN / m,。相反,考虑每桩射频,得出的结论是相反的:S = 2D 时,R2300kN(= 960kN / m*2.4m);S = 3D 时,R2660kN和 S =4D时,R2740kN。这就是为什么通常S = 4D是最具成本效益的解决方案。得到射频R的桩挠度也随S变化。
- = 4m的浅层滑动[图4(a)]的情况下,射频RF是稍微依赖桩间距。由于界面的深度相对较小,桩表现为刚性并响应得像挡土墙或沉箱那样。其结果是,群桩效应似乎并没有发挥重要的作用,射频RF和S几乎是独立的.但是,形成所需的射频RF所需要的桩弯矩M是不对的 ,这基本上取决于S(见以前的讨论)。
- 由于=8m深层滑动,滑动土体的厚度增加深[图4(c)],桩表现出柔性且群桩效应发挥越来越重要的作用。结果,RF对S更加敏感。因此,桩土系统的灵活性并不仅仅取决于桩间距,而主要是由滑动土体的深度决定。
图4:桩间距的影响;桩提供的关于桩头位移和最大弯矩M的射频RF与 (a)浅层滑坡=4m;(b)中间滑坡=6m;(C)较深层滑坡=8m有关
土壤不均匀性的影响
土壤的不均匀性的影响,根据剪切模量G随深度的分布,已被Kourkoulis 彻底研究(2009)。均质土层(即,常数G)与非均匀的相比,为便于比较,假设G随深度线性增加但与均质土保持相同的平均值。研究过程中,土壤的不均匀性的影响被认为是次要的。只有在 =4m的浅层滑动中,结果几乎不受影响。故关键的结论是,响应主要受不稳定层的强度,而不是刚度的分布影响。
基础稳定地面强度和刚度的影响
用模型材料,从相对松散的砂到岩石类材料,参数化研究分析基础稳定地面的强度和刚度 。稳定的地面层的理想土壤如下:
1.松散粉砂:
2.密砂:
3.软岩:
4.岩石:
从稳定土层的强度参数进行选择,最终使稳定土层提供的被动土压力大于或等于不稳定层中发展的极限土压力。对于无粘性土,后者是由(Broms 1964)给出:
(1)
式中的参数为9-12之间(Matlock1970)。
因此,这四个理想化的稳定土得出的强度参数比率/(Kourkoulis 2009):
1.对于松散粉砂: =;
2.对于密砂:=1.6;
3.对于软岩:=3 ;还有
4.对于岩石:=6
在所有研究案例中,桩进入稳定层的埋置深度被假定等于2,所以可以保证条件完全不变(虽然这样的深度对岩石是不必要的)。
图5:稳定土的刚度和强度的影响;比较三个理想化的稳定的壤层:(a)根据桩头位移桩头提供频射RF;(b)根据最大弯矩M的频射RF;(c)随深度分布的桩弯矩M
如图5所示的例子,分析揭示了桩嵌在强度相对较低的底层(密砂)时不能提供与当嵌入在刚性下卧层(岩)时相同水平的最大RF,除非是变形过度。然而,这增加的位移[图5(a)]与桩弯矩增加比例不相关[图5(b)]。因为较弱的土壤下卧层的剪切强度是被沿桩的长度、桩分布在几乎整个长度的挠度所动员,从而
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[150081],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


