
英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
结构风荷载(第三版)
————约翰·霍姆斯
第5章共振的动态响应和有效的静载荷分布
5.1介绍
由于风速的湍流特性存在于所有类型的风暴中,作用于结构的风荷载也时常会大幅波动。这就有可能激发结构的动态共振响应,或仅是部分结构,这些结构的自振频率小于1 Hz。结构的共振响应引入了一个时间的并发症历史效应,其中在任何时间的反应不仅取决于瞬时风阵风速度,或压力、沿结构作用,而且与前一次的历史的阵风或压力有关。
本章将介绍基本原理和风的动态响应的分析。对于气弹和疲劳影响的相关讨论也包括在内。此外,在本章中,还引入了等效或有效静风荷载分布的方法。
对动态响应的处理一直贯穿于和高层建筑紧密相关的第9章到第12章中、大屋顶和体育场馆、修长的塔楼和桅杆和桥梁,重点在于这些结构的具体特征。在第15章,动态响应的法规途径将会被考虑到。
5.2动态响应的原理
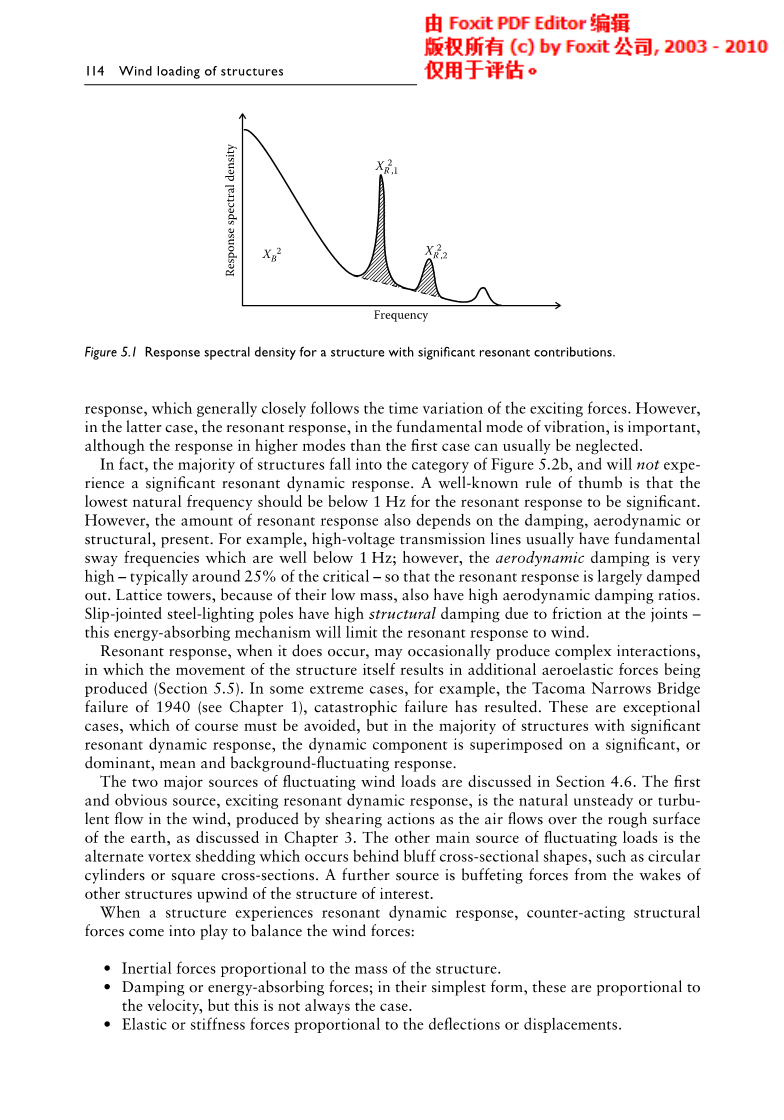
正如在第三章和第四章中讨论的那样,风速、压力和力量的波动性可能导致结构或者部分结构显著共振振动响应的激发,他们提供的固有频率和阻尼足够低。该共振的动态响应应该从所有结构承受的背景波动中区别出来。图5.1显示了风致响应下的结构动力响应谱密度;整个曲线下的面积代表总的均方跟波动响应(注意平均响应不包含在该区域)。与前两阶振型对应的共振响应用阴影表示在该图中。图5.1中的内容绝大部分来源于背景响应,这主要是由低于振动最低固有频率的低频率部分组成,并且,从实际情况来看,通常是在沿风荷载的情况下占主导地位作为来源的。共振的效应越来越显著,最终将占据主导的地位,当结构在相对于其宽度变得更高或更长时,它们的固有频率也会随之变得更低。
图5.1响应谱密度与显著谐振贡献的结构
图5.2a描述了顺风(拖)力随时间历程的变化特点;对于具有较高固有频率的结构的结构响应如图5.2b中所示,而具有低自然频率的结构响应如图5.2c所示。在前一种情况下,谐振,或振动组件,显然在响应过程中起着较为次要的作用,这通常与激励力的时间变化密切相关。然而,在后一种情况下,谐振响应在基本振型中是很重要的,尽管在高阶振型下的响应相比于第一阶振型通常可以忽略不计。
事实上,多数结构都属于图5.2b中描述的类别,并且将不会经历一个显著共振的动态响应过程。众所周知的规则就是,谐振响应的最低固有频率应低于1赫兹从而能够变得显著。然而,谐振响应的数目也取决于阻尼、空气动力学或者结构上的影响因素。例如,高压输电线路中的频率通常也有低于1赫兹的基本波动情况;然而,气动阻尼会非常高-通常约为25%左右-使得共振响应能够大幅度地不断衰减。由于它们较低的质量,格塔也具有很高的气动阻尼比。滑接合钢照明磁极具有高结构阻尼,这是由于在接头处的摩擦-此能量吸收机制将限制风的谐振响应。
图5.2 (a)的风力,(b)用高固有频率的结构的响应,以及(c)具有低固有频率的结构的响应时间历程
当共振反应发生的时候,它可能会偶尔产生复杂的相互作用,正是结构本身的运动导致了附加气动弹性力的生产(5.5节)。在一些极端情况下,例如,塔科马海峡大桥在1940年(见第1章)被破坏,从而导致了灾难性的后果。这些都是必须避免的特殊情况,但在大多数发生显著共振响应的结构之中,动态成分都被叠加在显著的、占据主导地位的、平均的和背景波动下的反应里面。
脉动风荷载的两个主要来源都在4.6节中进行了讨论。第一个显著刺激共振的动态响应来源,就是天然不稳定的或紊乱的风中气流,这是通过类似于空气在粗糙的地球表面流动的剪切作用产生的,就如同在第3章中讨论的那样。负荷波动的另一个主要来源是发生在流线形截面之后的交替涡旋脱落,例如圆形汽缸或正方形横截面。除此之外的来源是来自于其它结构尾流逆风向上的冲击力量。
当结构发生共振的动态响应时,抵消结构的力量就会开始发挥作用,以达到平衡风荷载的目的:
bull;惯性力与结构的质量成正比。
bull;阻尼或者消耗能量的力;在其最简单的形式中,与速度成正比关系,但也并非总是如此。
bull;弹性力或刚性力与挠度以及位移成正比关系。
当结构发生动态响应的时候,也说明了谐振响应是显著的,要记住的重要原则是,对于该结构的情况,挠度在任何情况下不仅取决于当时作用的风荷载,还与历史作用的风荷载相关。在准静态加载的情况下,结构随时都会即刻对荷载作出直接反应。
由于荷载中谐振部分的存在(第5.4.4节),有效载荷分布通过惯性力沿着所述结构的分布 给出了一个很好的近似值。这是基于一旦形成稳定的振幅,在谐振频率下波动风力大致平衡于阻尼力的假设。
在这一点上,值得注意的是结构对风和地震的动力响应之间具有本质的区别。这两种自然现象产生的激励作用之间的主要差别如下:
1.地震和风暴相比是一个持续时间短很多的过程(当然也有龙卷风作用的例外),因此地震被视为瞬态负载。
2.地震地面运动的卓越频率一般是充分发展的风暴频率的10-50倍。这也就意味着结构将在不同的方式受到影响,例如,在一定的高度范围内的建筑可能不会发生显著的风致响应,但是可能会对地震激励产生动力响应。
图5.3 由风和地震作用结构激励的各种频率范围
3.地震地面运动将会以完全相关的相当力作用于高层结构一定高度的形式呈现。然而,风暴中的涡状结构产生了作用于结构此高度处的风荷载。作用于细长结构的涡流状荷载也不是完全与高度相符合。
图5.3显示了在风荷载和地震作用下结构动力响应的不同频率范围。
5.3随机振动和光谱方法
在20世纪60年代的一些重要文件中,达文波特A.G.提出了一种基于随机振动理论(达文波特,1961年,1963年,1964年)研究结构风致振动的方法。美国罗德岛州的哈里斯(1963)和B.J.维克瑞(1965、1966)对这种方法的相关发展作出了重要的贡献。
该方法使用平稳随机过程的概念来描述风速度、风压和风力。这也就能假设自然界的复杂性是这样的,我们无法用言语来完美地(或确定地)形容、或预测由风暴产生的荷载作用。但是,我们能够使用平均量,如标准差、相关性和谱密度(或“谱”)来描述这两个令人兴奋的力量和结构响应这两个主要特征。谱密度已经在第3.3.4节和图5.1中介绍过,它被认为是该方法中最重要的因素,主要用于在频域分析方法中执行计算过程,也可以被称为光谱方法。
图5.4 随机振动(频域)的方法来谐振的动态响应。(达文波特自,1963年A.G.结构由阵风的抖振。论文集,国际会议风对建筑物,构筑物,特丁顿,英国,6月26日至28日,358-91。许可。)
风速、压力和由此产生的结构响应通常被作为平稳随机过程,该过程中的时间平均成分或平均组分要从变动成分中分离出来。因此
(5.1)
其中表示风的速度分量,压力(相对于测得的所定义的基准静压)或结构的响应,如弯矩,应力结果,扭转等;为平均或时间平均的部分;而是变动成分,使得= 0。如果x是一个响应变量,x(t)应当包括从该结构的振动的任何天然模式的激发所引起的任何共振的动态响应。
图5.4(达文波特之后,1963年)用图示说明的光谱方法的元素。主要计算在底行进行,其中,所述总均方波动响应从谱密度,或“光谱”的响应计算中完成。后者是从空气动力计算得出的,也就是说,反过来从风湍流度和阵风频谱中计算得出。频率依赖于空气动力学和机械导纳函数形成这些光谱之间的联系。对于具有低自振频率的结构,共振频率的扩增将会导致均方波动和峰值响应比具有较高自振频率的结构更高的情况,如同先前在图5.2中所示的那样。
平稳随机过程和公式5.1适用于大型风暴,如温带和热带气旋大风。它可能不适合一些短期、短暂的风暴,比如下击暴流或龙卷风等。这些类型的风暴研究方法仍在发展之中。
5.3.1顺风向单自由度结构的动力响应
我们将首先考虑小型结构的顺风动态响应,其动力特性由一个简单的质量弹簧阻尼器(图5.5)表示,并且在其中做不显著的湍流运动。这是一种单自由度系统,并合理地用一个大质量的结构支撑代替,诸如照明塔或桅杆在顶部灯的一列。这个系统的空气动力学阻力方程,即D(t),由公式5.2给出。
(5.2)
对于小结构的准稳态假设(4.6.2节)需要均方波动阻力之间的关系,也需要脉动纵向风速的写入:
(5.3)
方程5.3是类似的公式4.16的压力。
以频谱密度表示的方法写下方程5.3,
于是:
(5.4)
为了导出与该结构的响应波动的力之间的关系,以图5.5的简单的动态系统为代表,偏转首先被分成平均和波动分量,如公式5.1中所示:
(5.1)
图5.5 结构的简化动态模型
平均拉力,,和平均扭转,之间的关系如下:
(5.5)
其中,图5.5中的k是弹簧刚度。
偏转的光谱密度与所施加的力的频谱密度如下:
(5.6)
其中,| H(N)| 2被称为单自由度动力系统的机械导纳,由公式给出5.7。
(5.7)
| H(N)|,即机械导纳的平方根,也可以识别为动态放大系数或动态放大系数,它产生的时候
单自由度系统响应于谐波,或是正弦激振力。是无阻尼固有频率,而eta;是阻尼系数,C为临界阻尼,如图5.5所示。
通过组合等式5.4和5.6,偏转响应的频谱密度可以与风速波动的频谱密度相关联。
(5.8)
公式5.8应用于具有相对大气湍流尺度较小的前额区域结构。
对于较大的结构,速度波动不会在迎风面以及它们的整个相关区域同时发生,A,必须加以考虑。考虑到这一点的影响,空气动力导纳被引入其中,也就是。
从方程5.5中代入,
(5.9)
对于不会在较大程度上扰乱流动的开放式结构,比如格子框架塔,X 2(n)可以通过迎风速度波动的相关特性来加以确定(见第3.3.6)。这一假设也适用于固体结构,而X (2)也已经通过实验得到。
图5.6 气动导纳 - 实验数据和拟合函数。 (摘自维克里,B.J.1965年。在粗格栅和大气湍流中有关风荷载建筑物的研究模型中使用后面的流体。航空报告1143,国家物理实验室,英国;维克里,1968年B.J. ASCE的杂志工程力学部,94:31-46)
图5.6显示了用一个经验函数得到的相关实验数据。可以看出在低频情况下和针对小结构时X(N)趋向于1.0,低频阵风都几乎完全相关,并完全包络结构的面。对于高频率的情况,或是针对非常大的结构,由于相关性的缺乏,阵风在结构上产生的总荷载不起作用,并且气动导纳也趋向于零。
为了得到由公式5.9给出的均方波动偏转,偏转的频谱密度被绘制在所有频率范围内。
(5.10)
方程5.10被积下方的区域可以由两个分量分别(图5.7)来近似描述,也就是B和R,它们分别代表背景和谐振部分。
因此,
(5.11)
其中,
(5.12)
(5.13)
图5.7 背景和响应的谐振元件
方程5.11的近似是基于图5.7的共振峰中的假设,函数X 2(N),S U(n)分别为值X2(N 1)和值S U(N 1)不变。这是能较好地近似为平坦光谱密度风荷载的特性,而当共振峰很窄的时候,阻尼低时它就会发生(阿什拉夫阿里和古尔德,1985年)。
方程5.11的近似被各规范广泛应用于评估沿风响应的方法,并在第15章中做出了进一步的讨论。
背景因子B表示该结构的固有频率低于阵风准静态响应。很重要的一点是,它是与频率无关的,如公式5.12所示,其中频率仅仅被用于被积过程中,并且因此“综合得出”。对于很多风荷载作用下的结构,B被认为比R要大得多,即背景响应相比于谐振响应比较占优势。图5.2b就列举出了这种结构响应过程的一个例子。
5.3.2阵风响应因子
阵风响应因子是风工程中常用的术语。术语阵风加载因子被达文波特(1967年)引用,而维克里(1966年)使用了阵风因子这一术语。 这些术语基本上具有相同的含义,虽然有时候该因子应用于有效施加载荷,而有时还被应用于结构的响应。术语“阵风系数”能更好地符合风速本身的情况(第3.3.3节)。
阵风响应因子G可以被定义为预期的最大响应的比率(例如,偏转或应力)在一个定义
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[151289],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


