
英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
在役扩散板梁桥的实验研究
摘要:最近在德克萨斯州开发和实施了一类新型的平板梁桥梁,由缺少适当的设计指导,力矩和剪切设计是基于那些扩展的箱梁桥。然而它们的适用性仍然存在问题。为了开发新的标准,研究了这种新桥系统的负载分布特性。对位于美国69号丹尼森的在线扩建平板梁桥进行了全面的静态和动态测试,使用各种实验方法来推断由重载卡车产生的单个梁的抵抗力矩和剪力。将实验导出的负荷分布因子(LDFs)与精细有限元模型预测进行比较,获得了令人满意的协议。观测到的桥梁响应在动态载荷下超过目前的设计规格影响因子为33%,因此对于维修负荷设计,推荐允许的拉伸应力稍微降低一点。
- 绪论
在德克萨斯州和其他地方,预应力混凝土板梁桥作为一种有效的解决方案,用于简支的跨度达15米。然而设计经验表明,与常见的传统预应力混凝土I型梁桥相比板梁桥的成本更高。为了探索具有浅层深度的短跨度桥梁经济实用的设计解决方案,德克萨斯交通部最近开发了一种称为平板梁桥的新型桥梁。由于没有具体的指导方针,TxDOT考虑了扩展箱梁桥相同的概念和设计标准。负载分布因子(LDF)是否对扩散板梁桥有效是否仍然未知。因此作者已经进行了双重实验和分析调查以探索普通平板梁桥的实验性能特别是负载分布行为。本文重点介绍了插入式平板梁桥的实验性能评估。
由于结构中的高度不确定性,对板桥对梁桥的分析是一个复杂的问题板梁对桥梁的分析是一个复杂的问题,因为结构的不确定性很大。自20世纪30年代以来,桥梁工程师利用LDFs的概念来确定单个梁的力矩和剪力,这对于新桥设计或现有桥梁评估是必要的。1991年,Zokaie等[1]开发了功率函数公式来计算特定类型的桥梁结构的LDF值,并且它们被AASHTO LRFD桥梁设计规范[2]快速采用。由于目前没有用于桥梁的平板梁梁类的LDF方程,设计人员需要采用类似桥梁类型的LDF公式,如扩展箱梁桥[3],但其适用性是未知的。在开发设计标准时,非常希望进行实验测试以进行验证。以前在有限数量的桥梁上进行现场实验。 已经进行了不同桥梁类型的力矩LDF值的实验测定,包括扩展箱梁桥[4],钢梁桥梁[5],实心板桥梁[6]和预应力混凝土桥梁桥梁[7,8]。
目前,TxDOT倾向于使用预制钢筋混凝土板梁和现场浇筑的钢筋混凝土板,并采用现场预制混凝土形式来建造这种新型的平板梁桥。这样的施工成本相对较低,制造和运输方便。然而由于深度为305毫米(12英寸)或381毫米(15英寸)深的浅板梁梁段的偏心率有限,所以扩展的平板梁桥系统被限制在跨越15米。但是可以通过使用后张预应力筋并采用负载平衡概念来实现更长的跨度[9,10]。
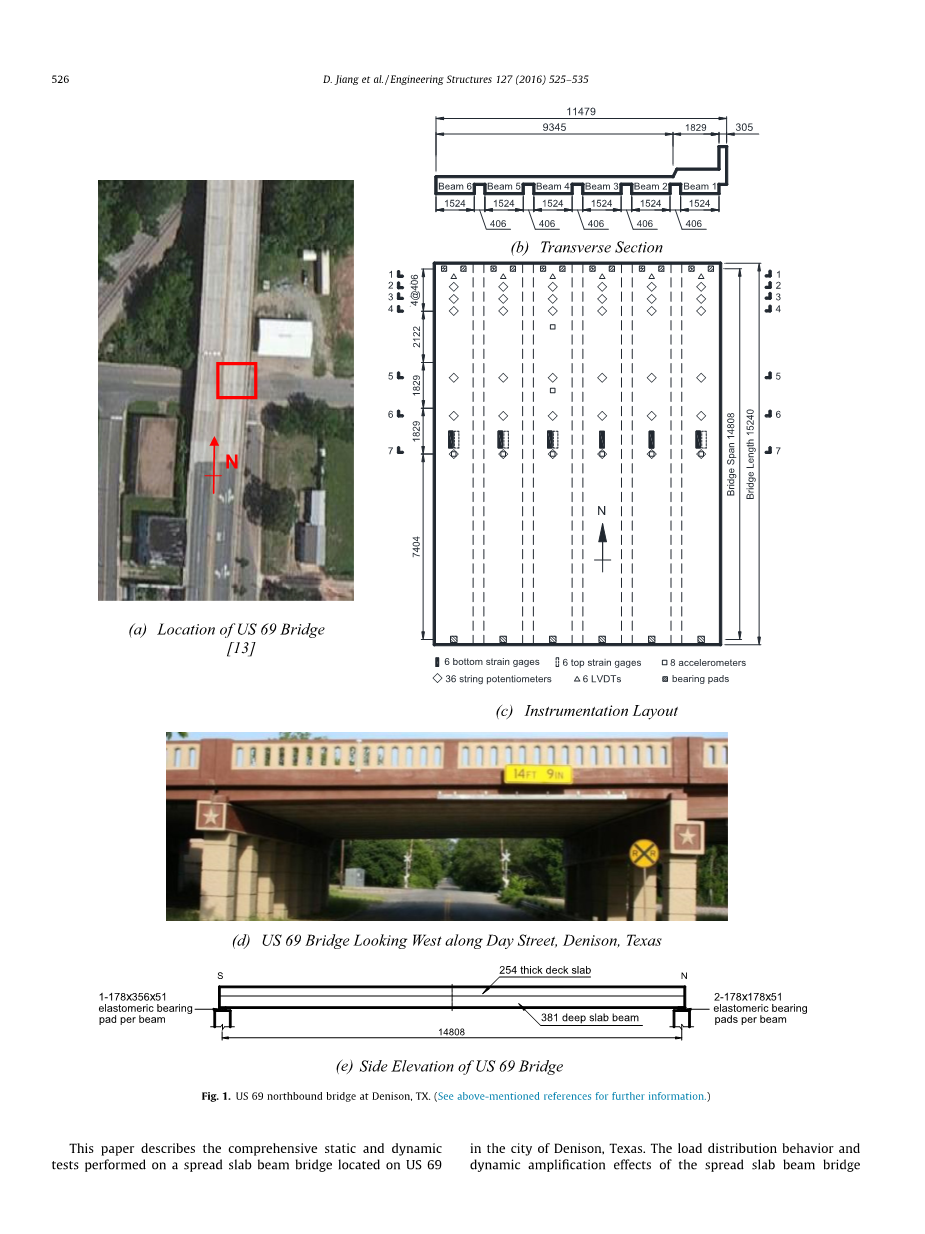
(b)横断面
美国69桥的位置[13] (c)仪表布局
(d)美国得克萨斯州丹尼森市的Day Street街69号
(e)美国69桥的高架
- 桥梁的描述
图1列出的是位于美国得克萨斯州的丹尼森的一部分69公路,美国69桥由18个跨度组成,南基础附近的前个跨度是由平板梁组成。第三个跨越日间街(图1)。改善日街道巷道的设计人员选择了由六层板组成的桥面板梁如图1所示。图1(b)测试的平板梁横跨长15.2米,宽11.5米(图1(c))。总体五车道美国69桥已经建成了两个相似的并排对称结构具有一个结构北行车道和南行其他结构车道;在桥的两半之间存在一个25毫米的接缝。该桥被装在图1所示的位置。图1(c)轴承座的中心线之间的跨距长度简支桥为14.8米如图1所示。平板梁是预制预紧5SB15混凝土段,它们宽1.52米(5英尺),厚381毫米(15英寸)。结构图表明钢筋混凝土的厚度平板梁顶部的克里特岛甲板为305毫米。因为平板梁之间的间距相对较小(406毫米),门控钢板被用作之间的停留形式平板梁支撑203毫米厚的就地(CIP)甲板板。然而由于预紧板梁的弯度基于中跨的甲板厚度约为254毫米现场观察。28天混凝土5SB15板梁和CIP甲板的抗压强度分别为37MPa和28MPa。
3实验方法
3.1仪表
图1(c)描述了美国69桥的测试跨度的仪表布局的平面图。对美国69号桥梁平台横梁台阶跨越Day Street进行了全面的静态和动态试验,以评估一般的在役性能,并具体研究桥梁系统的板梁之间的力矩和剪力分布。在桥梁跨距处安装了十二个应变仪(TML PL-60-11-3LT),以推断车辆载荷下的力矩LDF:其中六个安装在每个平板梁的拱腹表面上,三个安装在梁的顶面4-6,另外三个安装在人行道和护栏表面(图1(c)),将LVDT连接到北弯板的表面,靠近板梁下的北支撑处的每个轴瓦,测量其变形,从而推断剪切LDFS。另外,在北墩支撑和中跨之间分布的六个车站的平台梁的底面安装了36个串电位器,以获得该半跨的桥偏转场。串电位器测量相对于桥下面的路面。为了在移动的卡车载荷下捕获桥梁的模式形状和固有频率,将总共八个加速度计固定在平板梁的拱顶上;六个位于每个平板梁的中跨位置,其余两个连接到中跨和北部支撑之间的梁4。在现场测试中采用了62通道数据采集系统,采样速率设定在500Hz
3.2静态测试
图2(b)和(c)所示静载荷“试验”的详细情况列于表1中。静态试验由校准的自卸车沿跨度的各种排列施加如图1所示。由TxDOT谢尔曼地区办事处提供的装满沥青基料的自卸车。在美国75号附近的Denison称重站测量单个轴载荷; 图2(a)显示了测试自卸车的测量轴间距和车轴载荷。显示了临界时刻和剪切载荷情况下的车辆位置。为了研究外板和内板梁的力矩和剪切力矩,进行了一系列静态试验,包括两个纵向位置和五个横向位置。在纵向方向上当所得到的负载和最接近所得负载的轴载荷时,观察到最大弯矩距离中跨距离相等。在St. Venantsprinciple指导下,当最后一个轴载荷被放置在等于轴承垫中心的光束深度(0.6米)的距离时,观察到最大的剪切力。
根据AASHTO [3],对于横向,当两辆并排车辆可能存在1.2 m最小距离时,采取关键力矩和剪切。 鉴于在现场试验期间只有一辆自卸车可用,车辆以不同的横向对准停放,并且在数据分析期间采用叠加方法计算双车道负载反应。
外部平板梁最关键的位置是当两辆卡车尽可能靠近桥梁的西边(对齐1和2)停靠时。然而中间分隔带的存在阻止了测试车辆跨越桥中心,因此对准1的时刻与坐标2-5略有不同,如图1所示。
对于内部平板梁,两个车辆装载在对准3和4中以得到可能的最大LDF值。将车辆停放在尽可能靠近人行道路边的路线5进行考虑以研究复合材料甲板,人行道和栏杆。
3.3受控动态测试
评估动态效果的个体测试列于表2中。右侧和中间车道位置如图1所示。2进行受控动态载荷试验,以确定当车辆以不同速度通过桥梁时的动态放大效应。这些测试在获得桥梁的固有频率和模式形状方面也是有用的。在控制的动态负载测试期间,自卸车以特定的速度沿两个车道的每一个行驶。在进行动态试验之前,将甲板表面上的应变计电缆拆下,剩下的仪器在桥上记录结构响应。为了比较桥梁静态和动态响应的目的,还进行了停泊的车辆的参考静载荷情况以及沿着两个不同车道的剪切关键位置。雷达枪被用来测量越过桥梁时的车速。对于参考静载荷情况,与两个不同通道对齐的力矩和剪切临界位置如图1所示。
|
测试数目 |
车辆位置 |
目的 |
|
- 1 2 - 3 4 - 5 6 - 7 8 - 9 10 |
初始对齐5 中心对齐5 北对齐5 初始对齐4 中心对齐4 北对齐4 初始对齐3 中心对齐3 北对齐3 初始对齐2 中心对齐2 北对齐2 初始对齐1 中心对齐1 北对齐1 |
复合动作 内部梁 内部梁 外部梁 外部梁 |
表一静态负载测试协议
(a)试验车轴载荷和车轮间
(b)时刻临界位置:静态测试(c)剪切临界位置:静态试验
(d)时刻临界位置:受控动态测试(e)剪切临界位置:受控动态测试
|
测试数目 |
观测数据 |
车道 |
|
1 2 3 4 5 6 7 8 |
0 0 0 0 27 40 56 64 |
中(中) 中(北) 右(中) 右(北) 中 右 中 右 |
表二受控动态负载测试协议
3.4实验观察分析方法
载荷分布因子(LDF)g被定义为由于车辆载荷而在每个桥梁上产生的一般力矩或剪切作用与由于相同载荷而在隔离梁元件上产生的一般力矩或剪切作用的比率,并且由
=
其中Fi代表第i个束的时刻或剪切作用,F1D-Girder表示单个波束上的相应动作.
每个平板梁的力矩通常基于测量的应变值确定,然后通过比较每个梁的力矩分布来获得实验LDF值。
其中ebi表示第i束的底面上的混凝土应变;Mi是第i波束的时刻; Ii表示第i个波束的惯性矩; cbi表示中性轴与梁段底面之间的距离; E是杨氏模量; Sbi = Ii = cbi表示第i束的截面模数。
所使用的程序类似于Ghosn等人使用的方法。[12]和Kim [5]确定力矩分布因子,同时假设所有梁的截面模量相同,使得LDF等于应变值的比率。然而由于存在包括人行道和护栏的边缘加强构件,梁1的截面模数大于其他规则梁段的值; 这里的差异在此被考虑。
梁构件的中性轴的实验识别如图1所示。 通过在光束深度上假设线性应变分布,基于顶部和底部表面应变计读数,光束2-6的中性轴位置被确定为距离光束拱腹295mm,如图1所示。图3(b)。 基于CIP甲板和预制梁的设计混凝土强度的变形部分分析给出了离梁弯矩325 mm的理论中性轴位置,这接近测试值。
为了确定梁1附近的系统行为,在梁,人行道和护栏的表面安装了四个应变计,以调查复合作用行为的程度(图3(c))。 当卡车沿着对准5定位时,从应变计得到的结果也在图1中示出。 3(c),其中应变计值似乎不表现出平面截面行为。 根据设计图,在人行道和护栏之间的表面使用钢筋以提供界面剪切阻力。据推测,甲板,人行道和护栏是完全复合的。
基于在fc = 79 MPa下测得的早期混凝土强度,板梁混凝土的调整模量估计为Eb = 55GPa。 类似地,甲板混凝土模量估计为Ed = 33GPa。使用FEM的计算应变曲线也如图1所示。图3(c)。存在实验和计算结果之间接近。
在实验室中进行了一系列弹性轴承垫的静态和动态试验。 测量的载荷变形曲线表明:由于粘弹性效应表现出一些滞后行为,尽管在工作范围内垫片基本上是弹性的[11]。因此轴承垫被用作替代称重传感器,由此使用垫变形来推断剪切LDF。在现场试验期间,将六根LVDT连接到弯曲盖的表面,靠近每个平板梁下的北部支撑处的轴承瓦片,以测量其变形。 剪切中的第i个束的LDF由下式给出
其中Vi =第i个平板梁的反作用力(剪切力); K =支座垫块刚度; 并且di =第i个平板梁的支座垫块变形。
(a)梁2-6节 (b)变形梁2-6节
(c)梁1和人行道和护栏部分
3.5。 计算建模
有限元方法(FEM)用于创建轴承支座和桥梁跨度的三维模型,Abaqus(V6.13)用于所有分析。该模型基于设计图纸以及建立的现场测量尺寸进行建立。对于建模过程,采用C3D8R元件,它是一个具有三个自由度的线性八节点刚体单元,每个节点都采用。次要构件(人行道和护栏)的影响也完全考虑进模型。
图4显示了在主要静负荷情况下所有板梁的实验和计算偏转轮廓的比较。在桥面下方的串电位器测量中直接获得偏转,如图1中的开放符号所示。在北端附近测量的小偏转值显示出与计算出的偏差有些随机变化。这些偏差归因于测量质量和精度。总体而言有限元解法提供了与测量的偏转场的合理一致性; 对于大多数负载情况,差异通常小于0.3 mm。
也许比得到偏转场更复杂的是准确地模拟桥梁的动态特性。表3列出了桥跨的实验和FEM计算的前三个固有频率值(f1,f2和f3)的比较。在受控动态测试期间从加速度计读数中确定实验观察到的固有频
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[137907],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


